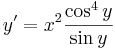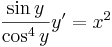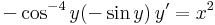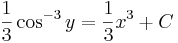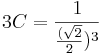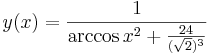Matematika A3a 2009/9. gyakorlat
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) (→Szeparábilis differenciálegyenlet) |
Mozo (vitalap | szerkesztései) (→Szeparábilis differenciálegyenlet) |
||
| 1. sor: | 1. sor: | ||
==Szeparábilis differenciálegyenlet== | ==Szeparábilis differenciálegyenlet== | ||
| − | + | '''1.''' Oldjuk meg az | |
:<math>y'=x^2\frac{\cos^4 y}{\sin y}</math> | :<math>y'=x^2\frac{\cos^4 y}{\sin y}</math> | ||
| − | :<math>y(0)=\frac{\pi}{4}</math> | + | egyenletet az |
| + | :a) <math> y(0)=-\frac{\pi}{2}</math> | ||
| + | :b) <math>y(0)=\frac{\pi}{4}</math> | ||
| + | :c) <math>y(0)=\frac{\pi}{3}+2\pi</math> | ||
| + | |||
| + | ''Mo.'' a) Ez egykonstans megoldás és nincs másik a (0,π/2)-n áthaladó, mert az y szerinti parciális derivált korlátos. | ||
| − | + | b) Az általános megoldásból keressük a kezdeti feltételt kielégítő megoldást: | |
:<math>\frac{\sin y}{\cos^4 y}y'=x^2</math> | :<math>\frac{\sin y}{\cos^4 y}y'=x^2</math> | ||
:<math>-\cos^{-4} y(-\sin y)\,y'=x^2</math> | :<math>-\cos^{-4} y(-\sin y)\,y'=x^2</math> | ||
:<math>\frac{1}{3}\cos^{-3} y=\frac{1}{3}x^3+C</math> | :<math>\frac{1}{3}\cos^{-3} y=\frac{1}{3}x^3+C</math> | ||
| + | Az implicit egyenlet: | ||
| + | :<math>\cos^{-3} y=x^3+3C</math> | ||
| + | Ha x=0 és y=π/4, akkor | ||
| + | :<math>3C=\frac{1}{\frac{(\sqrt{2}}{2})^3}</math> | ||
| + | és | ||
| + | :<math>y(x)=\frac{1}{\mathrm{arccos}\,x^2+\frac{24}{(\sqrt{2})^3}}</math> | ||
A lap 2009. november 16., 10:09-kori változata
Szeparábilis differenciálegyenlet
1. Oldjuk meg az
egyenletet az
- a)
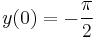
- b)
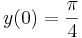
- c)
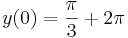
Mo. a) Ez egykonstans megoldás és nincs másik a (0,π/2)-n áthaladó, mert az y szerinti parciális derivált korlátos.
b) Az általános megoldásból keressük a kezdeti feltételt kielégítő megoldást:
Az implicit egyenlet:
- cos − 3y = x3 + 3C
Ha x=0 és y=π/4, akkor
és