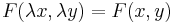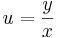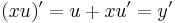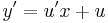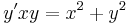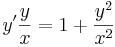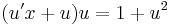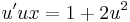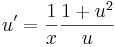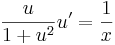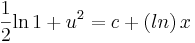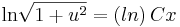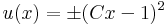Matematika A3a 2009/9. gyakorlat
Mozo (vitalap | szerkesztései) (→Szeparábilis differenciálegyenlet) |
Mozo (vitalap | szerkesztései) (→Szeparábilis differenciálegyenlet) |
||
| 20. sor: | 20. sor: | ||
:<math>y(x)=\mathrm{arccos}\frac{1}{\sqrt[3]{x^3+\frac{24}{(\sqrt{2})^3}}}</math> | :<math>y(x)=\mathrm{arccos}\frac{1}{\sqrt[3]{x^3+\frac{24}{(\sqrt{2})^3}}}</math> | ||
c) ugyanez + 2π | c) ugyanez + 2π | ||
| + | |||
| + | '''HF.''' Oldjuk meg az y' = sin(x) yln(y) egyenletet az | ||
| + | :a) y(0)=1, | ||
| + | :b) y(0)=e | ||
| + | kezdeti feltételek mellett! | ||
| + | ==Homogén fokszámú egyenlet== | ||
| + | Azt mondjuk, hogy az y' = F(x,y) egyenlet homogén fokszámú, ha | ||
| + | :<math>F(\lambda x,\lambda y)=F(x,y)\,</math> | ||
| + | A homogén fokszámú egyenlet megoldása visszavazethető a szeparálásra az | ||
| + | :<math>u=\frac{y}{x}\,</math> | ||
| + | új változó bevezetésével, ahol ''u'' = ''u''(''x'') az ismeretlen függvény. Ekkor | ||
| + | :<math>(xu)'=u+xu'=y'\,</math> | ||
| + | azaz | ||
| + | :<math>y'=u'x+u\,</math> | ||
| + | |||
| + | '''2.''' Oldjuk meg az | ||
| + | :<math>y'xy=x^2+y^2\,</math> | ||
| + | egyenletet! | ||
| + | |||
| + | ''Mo.'' Az új változóra történő áttérésnél az y<sup>2</sup>-nak már nem szabad szerepelnie az egyenletben, ezért, hogy ne féljen egyedül, szorozzunk be az egyenletet 1/x<sup>2</sup>-tel: | ||
| + | :<math>y'\frac{y}{x}=1+\frac{y^2}{x^2}\,</math> | ||
| + | :<math>(u'x+u)u=1+u^2\,</math> | ||
| + | :<math>u'ux=1+2u^2\,</math> | ||
| + | :<math>u'=\frac{1}{x}\frac{1+u^2}{u}\,</math> | ||
| + | ezt kell megoldani. Feltehető, hogy y(x) függvény nem veheti fel a nullát, így az u sem. Ekkor szeparálással: | ||
| + | :<math>\frac{u}{1+u^2}u'=\frac{1}{x}\,</math> | ||
| + | :<math>\frac{1}{2}\mathrm{ln}\,1+u^2=c+\mathrm(ln)\,x\,</math> | ||
| + | :<math>\mathrm{ln}\sqrt{1+u^2}=\mathrm(ln)\,Cx\,</math> | ||
| + | :<math>\sqrt{1+u^2}=Cx\,</math> | ||
| + | :<math>u(x)=\pm(Cx-1)^2\,</math> | ||
A lap 2009. november 16., 11:23-kori változata
Szeparábilis differenciálegyenlet
1. Oldjuk meg az
egyenletet az
- a)
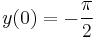
- b)
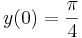
- c)
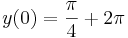
Mo. a) Ez egykonstans megoldás és nincs másik a (0,π/2)-n áthaladó, mert az y szerinti parciális derivált korlátos.
b) Az általános megoldásból keressük a kezdeti feltételt kielégítő megoldást:
Az implicit egyenlet:
- cos − 3y = x3 + 3C
Ha x=0 és y=π/4, akkor
és
c) ugyanez + 2π
HF. Oldjuk meg az y' = sin(x) yln(y) egyenletet az
- a) y(0)=1,
- b) y(0)=e
kezdeti feltételek mellett!
Homogén fokszámú egyenlet
Azt mondjuk, hogy az y' = F(x,y) egyenlet homogén fokszámú, ha
A homogén fokszámú egyenlet megoldása visszavazethető a szeparálásra az
új változó bevezetésével, ahol u = u(x) az ismeretlen függvény. Ekkor
azaz
2. Oldjuk meg az
egyenletet!
Mo. Az új változóra történő áttérésnél az y2-nak már nem szabad szerepelnie az egyenletben, ezért, hogy ne féljen egyedül, szorozzunk be az egyenletet 1/x2-tel:
ezt kell megoldani. Feltehető, hogy y(x) függvény nem veheti fel a nullát, így az u sem. Ekkor szeparálással:
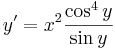
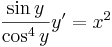
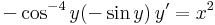
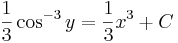
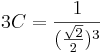
![y(x)=\mathrm{arccos}\frac{1}{\sqrt[3]{x^3+\frac{24}{(\sqrt{2})^3}}}](/upload/math/2/d/0/2d00fc36a69b3e76ac5fef5e80c7a2a3.png)