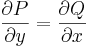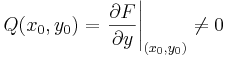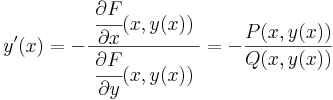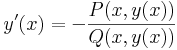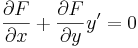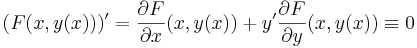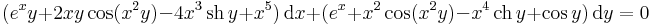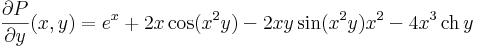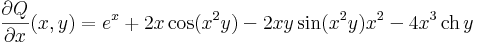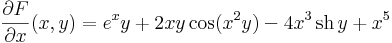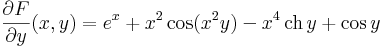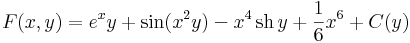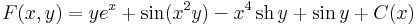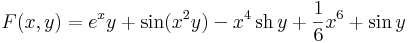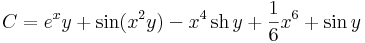Matematika A3a 2009/egzakt
Mozo (vitalap | szerkesztései) (→Példa) |
Mozo (vitalap | szerkesztései) (→Példa, elnevezés) |
||
| 10. sor: | 10. sor: | ||
:<math>y'=\frac{f(x)}{g(y)}\,</math> | :<math>y'=\frac{f(x)}{g(y)}\,</math> | ||
alakú szeparábilis differenciálegyenlet egzakt (''f,g'' folytonos, ''g'' sehol se nulla), hiszen ekkor a megoldásból: | alakú szeparábilis differenciálegyenlet egzakt (''f,g'' folytonos, ''g'' sehol se nulla), hiszen ekkor a megoldásból: | ||
| − | :<math>g(y)y'=f(x)\ | + | :<math>g(y)y'=f(x)\quad\quad\Rightarrow\quad\quad G(y)=F(x)+C</math> |
| − | + | :<math>\Phi(x,y):=G(y)-F(x)=C\quad\quad\Rightarrow\quad\quad\frac{\partial \Phi}{\partial x}=f,\quad\quad\frac{\partial \Phi}{\partial y}=g</math> | |
| − | :<math>\Phi(x,y):=G(y)-F(x)=C\ | + | |
| − | + | ||
| − | + | ||
Látható, hogy ekkor a megoldásokat implicit módon adja meg az | Látható, hogy ekkor a megoldásokat implicit módon adja meg az | ||
| 33. sor: | 30. sor: | ||
Tehát az egzakt egyenletben a (P,Q) függvény '''potenciálos'''. Ebből hasznos jellemzést kapunk a vektoranalízisbeli ismereteinkből. | Tehát az egzakt egyenletben a (P,Q) függvény '''potenciálos'''. Ebből hasznos jellemzést kapunk a vektoranalízisbeli ismereteinkből. | ||
| + | |||
==Egzakt egyenlet jellemzése és megoldhatósága== | ==Egzakt egyenlet jellemzése és megoldhatósága== | ||
'''Tétel.''' Legyen ''U'' egyszeresen összefüggő nyílt halmaz, ''P'',''Q'': ''U'' <math>\to</math> '''R''' folytonosan differenciálható függvények. A Pdx + Qdy = 0 egyenlet pontosan akkor egzakt, ha | '''Tétel.''' Legyen ''U'' egyszeresen összefüggő nyílt halmaz, ''P'',''Q'': ''U'' <math>\to</math> '''R''' folytonosan differenciálható függvények. A Pdx + Qdy = 0 egyenlet pontosan akkor egzakt, ha | ||
A lap 2009. november 22., 22:14-kori változata
Tartalomjegyzék |
Definíció
Azt mondjuk, hogy az
differenciálegyenlet egzakt, ha P,Q: U  R nyílt halmazon értelmezett függvények (Q sehol sem nulla) úgy, hogy létezik olyan F: U
R nyílt halmazon értelmezett függvények (Q sehol sem nulla) úgy, hogy létezik olyan F: U  R folytonosan differenciálható függvény, hogy
R folytonosan differenciálható függvény, hogy
Példa, elnevezés
Példa. Minden
alakú szeparábilis differenciálegyenlet egzakt (f,g folytonos, g sehol se nulla), hiszen ekkor a megoldásból:
Látható, hogy ekkor a megoldásokat implicit módon adja meg az
egyenlet, ami általában is így lesz ( F(x,y) = C ) ezért előnyös az egzakt forma.
Megjegyzés. Az egzakt differenciálegyenletet még
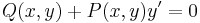 ill.
ill. 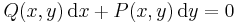
alakban is szokás írni.
Ez utóbbi egyenletetről azt is mondják, hogy akkor egzakt, ha a Q(x,y)dx + P(x,y)dy kifejezés teljes differenciál, azaz létezik olyan F(x,y) függvény, melynek teljes differenciálja:
Ezt mai jelölésekkel a következőképpen értelmezhetjük. Egy F kétváltozós függvény teljes differenciálja egy lineáris leképezés, mely a sztenderd {(1,0),(0,1)} bázisban felírt koordinátáival nem más, mit a parciális deriváltjainak sormátrixa:
Emiatt a (C) feltétel a következő alakban is írható:
![[\mathrm{d}F]=\left[P,Q\right]\,](/upload/math/3/4/3/343e00846494e553e629c9e57344a211.png) ill.
ill. ![\mathrm{grad}\,F=[P,Q]\,](/upload/math/4/f/9/4f9b9ba5601098c77e15e1f242d50948.png)
Tehát az egzakt egyenletben a (P,Q) függvény potenciálos. Ebből hasznos jellemzést kapunk a vektoranalízisbeli ismereteinkből.
Egzakt egyenlet jellemzése és megoldhatósága
Tétel. Legyen U egyszeresen összefüggő nyílt halmaz, P,Q: U  R folytonosan differenciálható függvények. A Pdx + Qdy = 0 egyenlet pontosan akkor egzakt, ha
R folytonosan differenciálható függvények. A Pdx + Qdy = 0 egyenlet pontosan akkor egzakt, ha
Az F függvényt, az Pdx + Qdy = 0 egyenlet első integráljának nevezzük.
Ezt a tételt jól ismerjük és a bizonyítását a vektoranalízisben vettük. Sokkal fontosabb azonban, hogy igazoljuk az egyenlet megoldhatóságát ebben az esetben.
Tétel. Legyen P,Q: U  R folytonosan differenciálható függvények, Q sehol se nulla, grad F = (P,Q) és (x0,y0) ∈ U. Ekkor
R folytonosan differenciálható függvények, Q sehol se nulla, grad F = (P,Q) és (x0,y0) ∈ U. Ekkor
- a Pdx + Qdy = 0 egyenletnek van a kezdeti feltételt egyértelműen kielégítő megoldása és
- az F(x,y) = C egyenlet (x0,y0)-n áthaladó implicit függvénye a Pdx + Qdy = 0 egyenlet y(x0) = y0 kezdeti feltételt kielégítő megoldása.
Biz. 1) Egzisztencia.
így az implicit függvény tétel szerint, egyértelműen létezik F-nek y=y(x) implicit függvénye az adott pontban és ennek deriváltja:
Tehát létezik megoldása és y egy megoldása az egyenéletnek.
2) Unicitás. Ha létezik megoldása az egyenletnek, akkor a
egyenlet a grad F = (P,Q) miatt
de mivel
ezért az integrálszámítás alaptétele miatt F(x,y(x)) egy konstans függvény, azaz y(x) implicit függvénye az F(x,y)=0 egyenletnek. Ez ez utóbbi egyértelmű, ezért a megoldás is.
Megjegyzés. Bár a szeparábilis egyenlet egzakt, de a fenti feltétel a megoldádás létezésére sokkal szigorúbb mint a szeparábilisé.
Példa
Oldjuk meg az
differenciálegyenletet!
Mo.
Tehát egzakt. Az egyenlet első integrálját megpajuk, ha megoldjuk az
parciális differenciálegyenlet-rendszert. A megoldást paraméteres integrálással kapjuk:
Innen:
Tehát az első integrál:
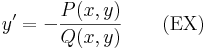
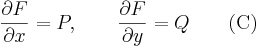
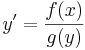
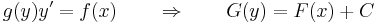
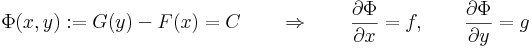
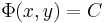
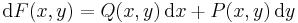
![[\mathrm{d}F(x,y)]=\mathrm{grad}\,F(x,y)=\left[\;\frac{\partial F}{\partial x}\;,\;\frac{\partial F}{\partial y}\;\right]](/upload/math/6/d/6/6d677f005d45feb13decbeb9f8433c81.png)