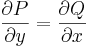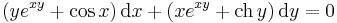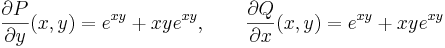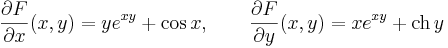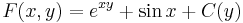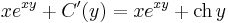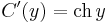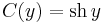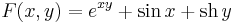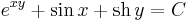Matematika A3a 2009/egzakt
Tartalomjegyzék |
Definíció
Azt mondjuk, hogy az
differenciálegyenlet egzakt, ha P,Q: U  R nyílt halmazon értelmezett függvények (Q sehol sem nulla) úgy, hogy létezik olyan F: U
R nyílt halmazon értelmezett függvények (Q sehol sem nulla) úgy, hogy létezik olyan F: U  R folytonosan differenciálható függvény, hogy
R folytonosan differenciálható függvény, hogy
Példa. Minden
alakú szeparábilis differenciálegyenlet egzakt, hiszen ekkor a megoldásból:
Látható, hogy ekkor a megoldásokat implicit módon adja meg az
egyenlet. Jelen esetben az F függvény deriváltja sehol sem nulla folytonos függvény, hisz F' = g ezért szigorúan monoton, emiatt kifejezhető y:
Azt is mondhatjuk, hogy ekkor
és az implicitfüggvény-tételre hivatkozhatunk. Ezt érdemes is felelevenítenünk:
Implicitfüggvény-tétel -- Ha az Φ: I×J  R folytonosan differenciálható függvény az (x0,y0) ∈ I×J pontban teljesíti a ∂Φ/∂y ≠ 0 feltételt és Φ(x0,y0)=0, akkor a Φ(x,y)=0 egyenletnek van az (x0,y0) ponton áthaladó implicit függvénye és ennek deriváltja:
R folytonosan differenciálható függvény az (x0,y0) ∈ I×J pontban teljesíti a ∂Φ/∂y ≠ 0 feltételt és Φ(x0,y0)=0, akkor a Φ(x,y)=0 egyenletnek van az (x0,y0) ponton áthaladó implicit függvénye és ennek deriváltja:
Egzisztencia- és unicitástétel
Tétel. Legyen P,Q: U  R folytonosan differenciálható függvények, Q sehol se nulla, grad F = (P,Q) és (x0,y0) ∈ U. Ekkor
R folytonosan differenciálható függvények, Q sehol se nulla, grad F = (P,Q) és (x0,y0) ∈ U. Ekkor
- a y'=-P/Q egyenletnek van a kezdeti feltételt egyértelműen kielégítő megoldása és
- az F(x,y) = C egyenlet (x0,y0)-n áthaladó implicit függvénye a y'=-P/Q egyenlet y(x0) = y0 kezdeti feltételt kielégítő megoldása.
Biz. 1) Egzisztencia.
így az implicit függvény tétel szerint, egyértelműen létezik F-nek y=y(x) implicit függvénye az adott pont egy környezetében és ennek deriváltja:
Tehát létezik megoldása és y egy megoldása az egyenletnek.
2) Unicitás. Ha létezik megoldása az egyenletnek, akkor a
egyenlet a grad F = (P,Q) miatt
de mivel az összetett függvény differenciálása miatt (d(F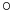 G)(u)=dF(G(u))
G)(u)=dF(G(u))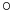 dG(u))
dG(u))
ezért az integrálszámítás alaptétele miatt F(x,y(x)) egy konstans függvény, azaz y(x) implicit függvénye az F(x,y)=0 egyenletnek. Ez ez utóbbi egyértelmű, ezért a megoldás is.
Megjegyzés. Bár a szeparábilis egyenlet egzakt, de a fenti feltétel a megoldádás létezésére sokkal szigorúbb mint a szeparábilisé.
Az egzaktság jellemzése
Megjegyzés. Az egzakt differenciálegyenletet még
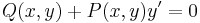 ill.
ill. 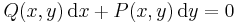
alakban is szokás írni.
Ez utóbbi egyenletetről azt is mondják, hogy akkor egzakt, ha a Q(x,y)dx + P(x,y)dy kifejezés teljes differenciál, azaz létezik olyan F(x,y) függvény, melynek teljes differenciálja:
Ezt mai jelölésekkel a következőképpen értelmezhetjük. Egy F kétváltozós függvény teljes differenciálja egy lineáris leképezés, mely a sztenderd {(1,0),(0,1)} bázisban felírt koordinátáival nem más, mit a parciális deriváltjainak sormátrixa:
Emiatt a (C) feltétel a következő alakban is írható:
![[\mathrm{d}F]=\left[P,Q\right]\,](/upload/math/3/4/3/343e00846494e553e629c9e57344a211.png) ill.
ill. ![\mathrm{grad}\,F=[P,Q]\,](/upload/math/4/f/9/4f9b9ba5601098c77e15e1f242d50948.png)
Tehát az egzakt egyenletben a (P,Q) függvény potenciálos. Ebből hasznos jellemzést kapunk a vektoranalízisbeli ismereteinkből.
Tétel. Legyen U egyszeresen összefüggő nyílt halmaz, P,Q: U  R folytonosan differenciálható függvények. A Pdx + Qdy = 0 egyenlet pontosan akkor egzakt, ha
R folytonosan differenciálható függvények. A Pdx + Qdy = 0 egyenlet pontosan akkor egzakt, ha
Az F függvényt, az Pdx + Qdy = 0 egyenlet első integráljának nevezzük.
Ezt a tételt jól ismerjük és a bizonyítását a vektoranalízisben vettük. Sokkal fontosabb azonban, hogy igazoljuk az egyenlet megoldhatóságát ebben az esetben.
Példa
Oldjuk meg az
differenciálegyenletet!
Mo.
Tehát egzakt. Az egyenlet első integrálját megkapjuk, ha megoldjuk az
parciális differenciálegyenlet-rendszert.
Az első egyenletből:
A második egyenlet miatt:
azaz
Innen a C(y)-ra egy partikuláris megoldás:
Azaz
Ez valóban teljesíti a grad F = [P,Q] feltételt, így az első integrál:
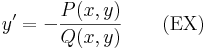
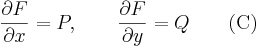
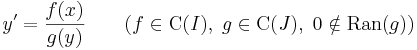
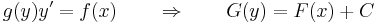
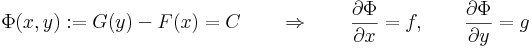
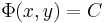
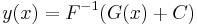
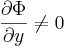
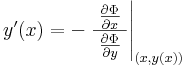
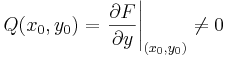
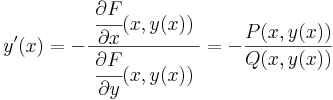
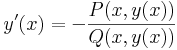
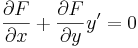
![(F(x,y(x)))'=[\mathrm{grad}\,F|_{(x,y(x))}]\cdot\begin{bmatrix}x'\\y'(x)\end{bmatrix}=\frac{\partial F}{\partial x}|_{(x,y(x))}+y'\frac{\partial F}{\partial y}|_{(x,y(x))}\,](/upload/math/8/9/9/899b820fe9c51c606292a75802e9b025.png)
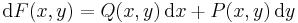
![[\mathrm{d}F(x,y)]=\mathrm{grad}\,F(x,y)=\left[\;\frac{\partial F}{\partial x}\;,\;\frac{\partial F}{\partial y}\;\right]](/upload/math/6/d/6/6d677f005d45feb13decbeb9f8433c81.png)