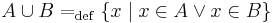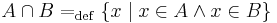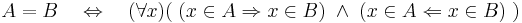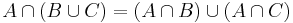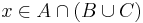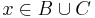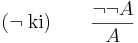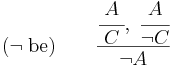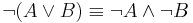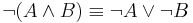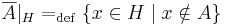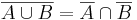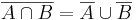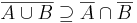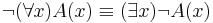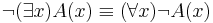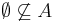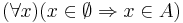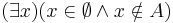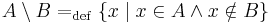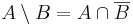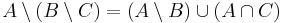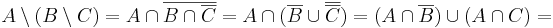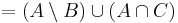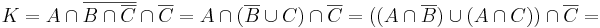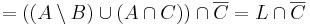Matematika közlek A1a 2013/2. gyakorlat
Tartalomjegyzék |
Példa
A fenti következtetésekre azonnal hozhatunk példát a halmazok témaköréből, ugyanis a halmazműveletek megfeleltethetők a logikai műveleteknek. A halmazoknál van egy kitüntetett nyitott mondat: ha H halmaz, akkor x ∈ H azt jelenti, hogy az alaphalmaz egy x-szel jelölt (esetleg közelebbről jobban meg nem határozott) eleme benne van a H halmazban. Legyenek A és B halmazok. Ekkor A és B uniója:
azaz azon elemek halmaza, mely az A illetve a B közül legalább az egyikben benne vannak;
A és B metszete:
azaz azon elemek halmaza, mely az A-ban is és a B-ben is benne vannak.
Ha választ várnánk arra a kérdésre, hogy mi az a halmaz, akkor szintén a matematikafilozófia ingoványában találnánk magunkat, ezért intellektuálisan a legtisztességesebb, ha tárgyunk célját (az analízis elsajátítását) érdeklődésünk homlokterébe tartva, ezzel a kérdéssel nem foglalkozunk.
Tudjuk: két halmaz egyenlő, akkor és csak akkor, ha ugyanazok az elemeik. Formulákban:
A nyilak a következtetés irányát jelzik. Az, hogy a "ha A akkor B" (jelben: A 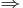 B) és az "A -ból következik B" (jelben:
B) és az "A -ból következik B" (jelben: 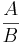 ) ugyanazt jelenti, az egyáltalán nem nyilvánvaló és valójában az úgy nevezett dedukciótétel mondja ki, persze bizonyos itt nem részletezett feltételek mellett.
) ugyanazt jelenti, az egyáltalán nem nyilvánvaló és valójában az úgy nevezett dedukciótétel mondja ki, persze bizonyos itt nem részletezett feltételek mellett.
1. Feladat. Igazoljuk a disztributív szabályt, legalábbis az egyiket, az alábbit:
Bizonyítás. 1) Vegyünk egy tetszőleges x-et. Igazoljuk: "ha x ∈ baloldal, akkor x ∈ jobboldal".
Esetszétválasztás jön, mert innentől nem tudjuk, x a B-ben vagy a C'-ben van
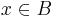
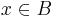 és
és 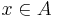 (igaz állítást bármihez "hozzáéselhetünk": és be)
(igaz állítást bármihez "hozzáéselhetünk": és be)
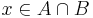
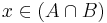 vagy
vagy 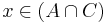 (bármi "hozzávagyolható" egy igaz kijelentéshez: vagy be)
(bármi "hozzávagyolható" egy igaz kijelentéshez: vagy be)
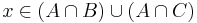
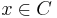
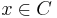 és
és 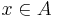 (igaz állítást bármihez "hozzáéselhetünk": és be)
(igaz állítást bármihez "hozzáéselhetünk": és be)
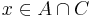
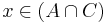 vagy
vagy 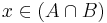 (bármi "hozzávagyolható" egy igaz kijelentéshez: vagy be)
(bármi "hozzávagyolható" egy igaz kijelentéshez: vagy be)
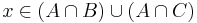
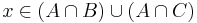 azaz mindkét esetben kijött a jobboldal.
azaz mindkét esetben kijött a jobboldal.
2) Visszafelé ugyanígy, csak felfelé.
Negáció, indirekt bizonyítás
A tagadás (negáció) kiküszöbölési szabálya az úgy nevezett kettős tagadás törlésének szabálya:
A bevezetési szabálya pedig az úgy nevezett redukció ad abszurdum.
Ezeknek a segítségével olyan fontos tételeket is levezethetünk, mint a De-Morgan azonosságok:
A fentiekben a  , hogy a két oldalon lévő kifejezés kölcsönösek következik egymásból.
, hogy a két oldalon lévő kifejezés kölcsönösek következik egymásból.
Példák
Ami még hiányzik a logikai operációk és a halmazműveletek megfeleltetéséből, az negáció halmazműveletekkel történő átfogalmazása, mely nem titok, a komplementerképzés lesz. Sajnos komoly logikai problémát okozna, ha komplementeren egy A halmaz esetén azon elemeket értenénk, melyek nem az A-ban vannak. Ekkor ugyanis egy kisebb halmaz, mint mondjuk az {1,2,3} komplementere a világ összes ezektől különböző dolgából állna. Ezzel azonban világos, hogy megint a matematikafilozófia ingoványos talajára tévednénk, így ezt másként tesszük.
Ha H halmaz, akkor az A halmaznak a H-ra vonatkozó komplementere az
Ha a fenti H halmazt alkalmasan nagynak választjuk, akkor elkerüljük a logikai problémát.
Ezzel a De-Morgan-azonosságok halmazokkal megfogalmazott változata a következő alakban írható:
A fenti egyenlőségek középiskolából ismert relációval is kifejezhetők. Azt mondjuk, hogy A része B-nek, ha minden olyan esetben, amikor egy elem eleme A-nak, akkor B-nek is eleme, jelben:
Azaz az, hogy A = B az ugyanaz, mint hogy 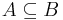 és
és 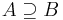 is teljesül.
is teljesül.
2. Feladat. Példaként nézzük csak a
esetet.
Megoldás. Vegyünk egy elemet a jobboldalból és igazoljuk, hogy benne van a baloldalban. Tudjuk a metszet definíciója miatt, hogy ekkor
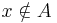
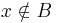
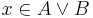 (indirekt feltevés), ezek után esetszétválasztáshoz kell folyamodnunk. Mindkét esetben ellentmondásra jutunk:
(indirekt feltevés), ezek után esetszétválasztáshoz kell folyamodnunk. Mindkét esetben ellentmondásra jutunk:
- ha
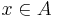 , akkor a legfelső
, akkor a legfelső
- ha
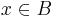 , akkor a legfelső alatti egyenlőség miatt jutunk ellentmondásra, így a
, akkor a legfelső alatti egyenlőség miatt jutunk ellentmondásra, így a
- ha
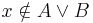 konklúzióra jutottunk.
konklúzióra jutottunk.
Egy másik jellegzetes példa a részhalmaz relációval kapcsolatos. Előtte azonban fel kell idéznünk a kvantrokra vonatkozó De-Morgan-azonosságot. A "létezik" szót (mely a "minden" duálisa) ∃-tel jelöljük:
A kijelentések világosak: ha nem minden dolog A, akkor van olyan dolog, ami nem A. Ha nem létezik A, akkor minden dolog nem A tulajdonságú.
3. Feladat. Igazoljuk, hogy az üres halmaz minden halmaznak része.
Megoldás. Legyen A tetszőleges halmaz. Indirekten tegyük fel, hogy
Az 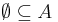 formulákban így néz ki:
formulákban így néz ki:
Egy ilyen tagadása az, hogy a kvantort átírjuk a duálisára és a tulajdonságot tagadjuk:
Ekkor azonban azt kaptuk, hogy létezik az üres halmaznak eleme, ami ellentmondás.
Boole-algebrai átalakítások
Világos, hogy az unióra és a metszetre a definíciójuk miatt ugyanazok az azonosságok vonatkoznak, mint a "vagy"-ra és az "és"-re. Ezeket a szabályokat Boole-algebrai azonosságoknak nevezzük. Ahhoz, hogy teljes legyen a kép még egy fontos halmazműveletet fel kell elevenítenünk: Legyenek A és B halmazok. Ekkor A mínusz B vagy A különbség B:
azaz azon elemek halmaza, melyek az A-nak elemei, de a B-nek nem.
Nagyon hasznos azonosság, hogy a különbség átírható komplementer és metszet segítségével:
ahol a komplementerképzés egy olyan halmazra vonatkoztatjuk, melyben minden szóban forgó halmaz részhalmazként benne van, például jelen esetben H = A U B alkalmas ilyen halmaz .
4. Feladat. Igazoljuk, hogy tetszőleges A, B és C halmazokra
Megoldás. Írjuk fel a baloldalt és alakítsuk addig, míg ki nem jön a jobboldal:
Cáfoló példák, cáfoló szituációk
Azt, hogy egy kijelentés igaz, azt a matematikában bizonyítással látjuk be. Például egy "ha A, akkor B" állítás esetén az A-ból levezetjük B-t.
Azt, hogy egy kijelentés hamis, általában cáfoló ellenpélda vagy cáfoló szituációra való rámutatással. Például egy "ha A, akkor B" állítás cáfolása esetén meg kell mutatunk, hogy a megadott cáfoló szituációban A ugyan igaz, de B nem. Ez azt jelenti, hogy ellenpélda esetén is kell bizonyítanunk, éspedig az előző esetben azt, hogy "bár A, de nem B". A metódus tehát a következő: 1) adunk egy példát 2) belátjuk, hogy az adott példa ellenpélda.
Példák
5. Feladat. Legyen A, B és C tetszőleges halmaz, továbbá legyen
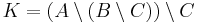 és
és
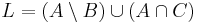
Vizsgáljuk meg, hogy melyik tartalmazás áll fenn!
Megoldás. Az A U B-re vonatkozó komplementerképzésre áttérve:
Tehát 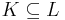 biztosan igaz, azaz (1) igaz.
biztosan igaz, azaz (1) igaz.
Ellenben (2) hamis, ellenpélda:
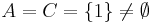 ,
,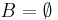
Ugyanis, ekkor 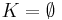 ,
, 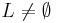 .
.
Házi feladatok
- K\(K\L) = L\(L\K)
- (K ∩ L) \ ( K\M ) = K ∩ L ∩ M
- (K\L)\M = (K\M)\(L\M)