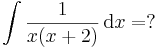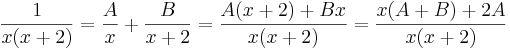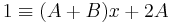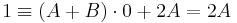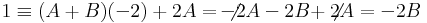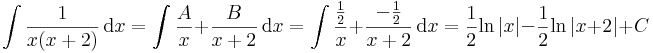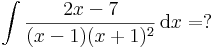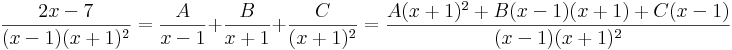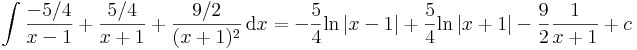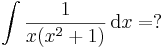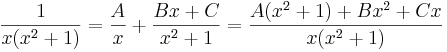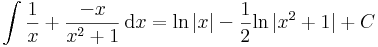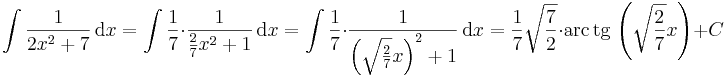Matematika közlek A2a 2014

A MathWikiből

(Változatok közti eltérés)

A lap 2014. február 16., 21:21-kori változata

1. gyakorlat

Házik: BaBcs. 12. fej.: 5, 24, 15, 70, 23, 68, 76, 90, 88, 158, 125, 138.

Órai:

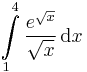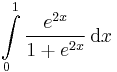integrálás helyettesítéssel: 65. $\int\limits_1^4\frac{e^{\sqrt{x}}}{\sqrt{x}}\,\mathrm{d}x$ , 48. $\int\limits_0^1\frac{e^{2x}}{1+e^{2x}}\,\mathrm{d}x$ , 34. $\int\limits_e^{e^2}\frac{1}{x\sqrt[3]{\mathrm{ln}\,x}}\,\mathrm{d}x$

a helyettesítéses integrálás formulájával: 25. 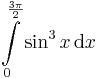$\int\limits_0^{\frac{3\pi}{2}}\sin^3 x\,\mathrm{d}x$ , 68'.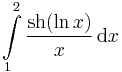 $\int\limits_1^{2}\frac{\mathrm{sh}(\mathrm{ln}\,x)}{x}\,\mathrm{d}x$

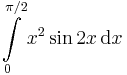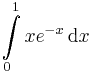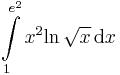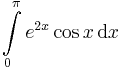
parciális integrálás: 78. $\int\limits_0^{\pi/2}x^2\sin 2x\,\mathrm{d}x$ , 83. $\int\limits_0^{1}xe^{-x}\,\mathrm{d}x$ , 90'. $\int\limits_1^{e^2}x^2\mathrm{ln}\,\sqrt{x}\,\mathrm{d}x$ , 86. $\int\limits_0^{\pi}e^{2x}\cos x\,\mathrm{d}x$

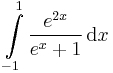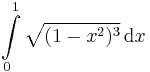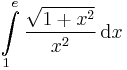további példák helyettesítéssel történő integrálásra: $\int\limits_{-1}^1\frac{e^{2x}}{e^x+1}\,\mathrm{d}x$ , $\int\limits_{0}^1\sqrt{(1-x^2)^3}\,\mathrm{d}x$ , $\int\limits_{1}^e\frac{\sqrt{1+x^2}}{x^2}\,\mathrm{d}x$ ,

2. gyakorlat

Házik: Babcs. később

Órai:

Racionális törtek integrálása:

A nevező egyszeres gyökökkel rendelkező elsőfokúak szorzata:

$\int\frac{1}{x(x+2)}\,\mathrm{d}x=?$

$\frac{1}{x(x+2)}=\frac{A}{x}+\frac{B}{x+2}=\frac{A(x+2)+Bx}{x(x+2)}=\frac{x(A+B)+2A}{x(x+2)}$

Gyökmódszer

$1\equiv(A+B)x+2A$

-ben először tegyük x-be az egyik gyököt, az 0-t:

$1\equiv(A+B)\cdot 0+2A=2A$

innen A=1/2, majd a másik gyököt:

$1\equiv(A+B)(-2)+2A=\;\;\not{\!\!\!\!-2A}-2B+\not{\!\!2A}=-2B$

azaz B=-1/2.

$\int\frac{1}{x(x+2)}\,\mathrm{d}x=\int\frac{A}{x}+\frac{B}{x+2}\,\mathrm{d}x=\int\frac{\frac{1}{2}}{x}+\frac{-\frac{1}{2}}{x+2}\,\mathrm{d}x=\frac{1}{2}\mathrm{ln}\,|x|-\frac{1}{2}\mathrm{ln}\,|x+2|+C$

A nevező többszörös gyökökkel rendelkező elsőfokúak szorzata

$\int\frac{2x-7}{(x-1)(x+1)^2}\,\mathrm{d}x=?$

$\frac{2x-7}{(x-1)(x+1)^2}=\frac{A}{x-1}+\frac{B}{x+1}+\frac{C}{(x+1)^2}=\frac{A(x+1)^2+B(x-1)(x+1)+C(x-1)}{(x-1)(x+1)^2}$

Ekkor a gyökmódszerrel: x=-1-re: -2C=2(-1)-7=-9, azaz C=9/2. x=1-re 4A=-5, A=-5/4 és egy szabadon válaztott egyszerű: x=0-ra: A-B-C=-7, ahonnan B=A-C+7, azaz B=-5/4-18/4+28/4= 5/4

$\int\frac{-5/4}{x-1}+\frac{5/4}{x+1}+\frac{9/2}{(x+1)^2}\,\mathrm{d}x=-\frac{5}{4}\mathrm{ln}\,|x-1|+\frac{5}{4}\mathrm{ln}\,|x+1|-\frac{9}{2}\frac{1}{x+1}+c$

A nevező egyszeres multiplicitású irreducibilis tényezők szorzata

$\int\frac{1}{x(x^2+1)}\,\mathrm{d}x=?$

Itt a keresendő alak:

$\frac{1}{x(x^2+1)}=\frac{A}{x}+\frac{Bx+C}{x^2+1}=\frac{A(x^2+1)+Bx^2+Cx}{x(x^2+1)}$

vegyes módszerrel: x=0: A=1 C=0, mert nincs a bal oldalon elsőfokú B=-A, mert másodfokú sincs.

$\int\frac{1}{x}+\frac{-x}{x^2+1}\,\mathrm{d}x=\mathrm{ln}\,|x|-\frac{1}{2}\mathrm{ln}\,|x^2+1|+C$

Kijöhetett volna az is, hogy C ≠ 0 pl:

$\int\frac{1}{2x^2+7}\,\mathrm{d}x=\int\frac{1}{7}\cdot\frac{1}{\frac{2}{7}x^2+1}\,\mathrm{d}x=\int\frac{1}{7}\cdot\frac{1}{\left(\sqrt{\frac{2}{7}}x\right)^2+1}\,\mathrm{d}x=\frac{1}{7}\sqrt{\frac{7}{2}}\cdot\mathrm{arc\,tg}\, \left(\sqrt{\frac{2}{7}}x\right)+C$

A nevező többszörös multiplicitású irreducibilis tényezők szorzata Ekkor 1) a parciális integrálásnál tanult rekurzív eljárással lehet a másodfokúak hatványait kiintegrálni.

@@ 1. sor: / 1. sor: @@
-'''1. gyakorlat'''
+==1. gyakorlat==
 Házik: BaBcs. 12. fej.: 5, 24, 15, 70, 23, 68, 76, 90, 88, 158, 125, 138.
@@ 13. sor: / 13. sor: @@
 további példák helyettesítéssel történő integrálásra: <math>\int\limits_{-1}^1\frac{e^{2x}}{e^x+1}\,\mathrm{d}x</math>, <math>\int\limits_{0}^1\sqrt{(1-x^2)^3}\,\mathrm{d}x</math>, <math>\int\limits_{1}^e\frac{\sqrt{1+x^2}}{x^2}\,\mathrm{d}x</math>,
-'''2. gyakorlat'''
+==2. gyakorlat==
 Házik: Babcs. később

Matematika közlek A2a 2014

A lap 2014. február 16., 21:21-kori változata

1. gyakorlat

2. gyakorlat

Nézetek

Személyes eszközök

Navigáció

Keresés

Eszközök