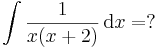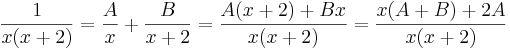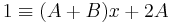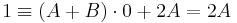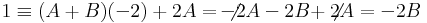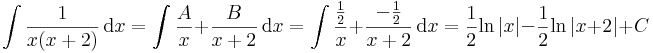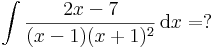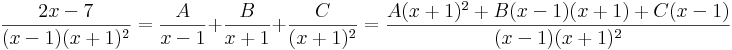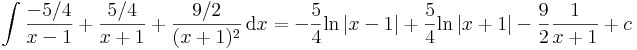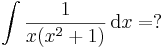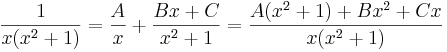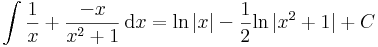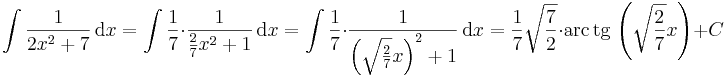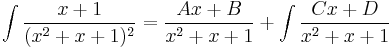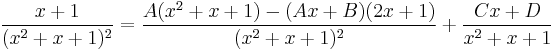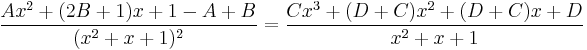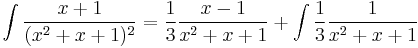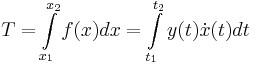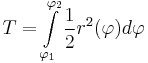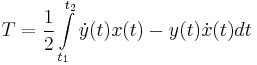Matematika közlek A2a 2014

A MathWikiből
(Változatok közti eltérés)
(→Az integrál alkalmazásai)
(→Az integrál alkalmazásai)
94. sor: 94. sor:
 
<math>P=2\pi\int\limits_a^bf(x)\sqrt{1+f'^2(x)} dx</math>
 
<math>P=2\pi\int\limits_a^bf(x)\sqrt{1+f'^2(x)} dx</math>
  
−
f(x)=
+
f(x)=\sqrt{x}
  
 
===Az improprius integrál===
 
===Az improprius integrál===

A lap 2014. február 23., 22:23-kori változata

Tartalomjegyzék

1. gyakorlat

Házik: BaBcs. 12. fej.: 5, 24, 15, 70, 23, 68, 76, 90, 88, 158, 125, 138.

Órai:

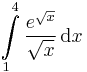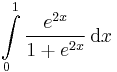integrálás helyettesítéssel: 65. \int\limits_1^4\frac{e^{\sqrt{x}}}{\sqrt{x}}\,\mathrm{d}x, 48. \int\limits_0^1\frac{e^{2x}}{1+e^{2x}}\,\mathrm{d}x, 34. \int\limits_e^{e^2}\frac{1}{x\sqrt[3]{\mathrm{ln}\,x}}\,\mathrm{d}x

a helyettesítéses integrálás formulájával: 25. 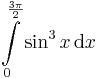\int\limits_0^{\frac{3\pi}{2}}\sin^3 x\,\mathrm{d}x, 68'.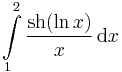 \int\limits_1^{2}\frac{\mathrm{sh}(\mathrm{ln}\,x)}{x}\,\mathrm{d}x

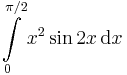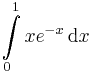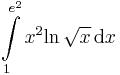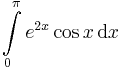
parciális integrálás: 78. \int\limits_0^{\pi/2}x^2\sin 2x\,\mathrm{d}x, 83. \int\limits_0^{1}xe^{-x}\,\mathrm{d}x, 90'. \int\limits_1^{e^2}x^2\mathrm{ln}\,\sqrt{x}\,\mathrm{d}x, 86. \int\limits_0^{\pi}e^{2x}\cos x\,\mathrm{d}x

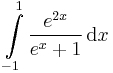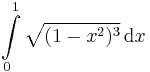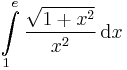további példák helyettesítéssel történő integrálásra: \int\limits_{-1}^1\frac{e^{2x}}{e^x+1}\,\mathrm{d}x, \int\limits_{0}^1\sqrt{(1-x^2)^3}\,\mathrm{d}x, \int\limits_{1}^e\frac{\sqrt{1+x^2}}{x^2}\,\mathrm{d}x,

2. gyakorlat

Házik: Babcs. 12. fej. 163, 165, 169, 13. fej. 16, 27, 56, 67, 147

Órai:

Racionális törtek integrálása

A) A nevező egyszeres gyökökkel rendelkező elsőfokúak szorzata:

\int\frac{1}{x(x+2)}\,\mathrm{d}x=?
\frac{1}{x(x+2)}=\frac{A}{x}+\frac{B}{x+2}=\frac{A(x+2)+Bx}{x(x+2)}=\frac{x(A+B)+2A}{x(x+2)}

Gyökmódszer

1\equiv(A+B)x+2A

-ben először tegyük x-be az egyik gyököt, az 0-t:

1\equiv(A+B)\cdot 0+2A=2A

innen A=1/2, majd a másik gyököt:

1\equiv(A+B)(-2)+2A=\;\;\not{\!\!\!\!-2A}-2B+\not{\!\!2A}=-2B

azaz B=-1/2.

\int\frac{1}{x(x+2)}\,\mathrm{d}x=\int\frac{A}{x}+\frac{B}{x+2}\,\mathrm{d}x=\int\frac{\frac{1}{2}}{x}+\frac{-\frac{1}{2}}{x+2}\,\mathrm{d}x=\frac{1}{2}\mathrm{ln}\,|x|-\frac{1}{2}\mathrm{ln}\,|x+2|+C

B) A nevező többszörös gyökökkel rendelkező elsőfokúak szorzata

\int\frac{2x-7}{(x-1)(x+1)^2}\,\mathrm{d}x=?
\frac{2x-7}{(x-1)(x+1)^2}=\frac{A}{x-1}+\frac{B}{x+1}+\frac{C}{(x+1)^2}=\frac{A(x+1)^2+B(x-1)(x+1)+C(x-1)}{(x-1)(x+1)^2}

Ekkor a gyökmódszerrel: x=-1-re: -2C=2(-1)-7=-9, azaz C=9/2. x=1-re 4A=-5, A=-5/4 és egy szabadon válaztott egyszerű: x=0-ra: A-B-C=-7, ahonnan B=A-C+7, azaz B=-5/4-18/4+28/4= 5/4

\int\frac{-5/4}{x-1}+\frac{5/4}{x+1}+\frac{9/2}{(x+1)^2}\,\mathrm{d}x=-\frac{5}{4}\mathrm{ln}\,|x-1|+\frac{5}{4}\mathrm{ln}\,|x+1|-\frac{9}{2}\frac{1}{x+1}+c

C) A nevező egyszeres multiplicitású irreducibilis tényezők szorzata

\int\frac{1}{x(x^2+1)}\,\mathrm{d}x=?

Itt a keresendő alak:

\frac{1}{x(x^2+1)}=\frac{A}{x}+\frac{Bx+C}{x^2+1}=\frac{A(x^2+1)+Bx^2+Cx}{x(x^2+1)}

vegyes módszerrel: x=0: A=1 C=0, mert nincs a bal oldalon elsőfokú B=-A, mert másodfokú sincs.

\int\frac{1}{x}+\frac{-x}{x^2+1}\,\mathrm{d}x=\mathrm{ln}\,|x|-\frac{1}{2}\mathrm{ln}\,|x^2+1|+C

Kijöhetett volna az is, hogy C ≠ 0 pl:

\int\frac{1}{2x^2+7}\,\mathrm{d}x=\int\frac{1}{7}\cdot\frac{1}{\frac{2}{7}x^2+1}\,\mathrm{d}x=\int\frac{1}{7}\cdot\frac{1}{\left(\sqrt{\frac{2}{7}}x\right)^2+1}\,\mathrm{d}x=\frac{1}{7}\sqrt{\frac{7}{2}}\cdot\mathrm{arc\,tg}\, \left(\sqrt{\frac{2}{7}}x\right)+C

D) A nevező többszörös multiplicitású irreducibilis tényezők szorzata Ekkor 1) a parciális integrálásnál tanult rekurzív eljárással lehet a másodfokúak hatványait kiintegrálni. 2) Osztrogradszkíj módszerével:

\int\frac{x+1}{(x^2+x+1)^2}=\frac{Ax+B}{x^2+x+1}+\int\frac{Cx+D}{x^2+x+1}
\frac{x+1}{(x^2+x+1)^2}=\frac{A(x^2+x+1)-(Ax+B)(2x+1)}{(x^2+x+1)^2}+\frac{Cx+D}{x^2+x+1}
\frac{Ax^2+(2B+1)x+1-A+B}{(x^2+x+1)^2}=\frac{Cx^3+(D+C)x^2+(D+C)x+D}{x^2+x+1}

C=0, A=D, D=2B+1, 1-D+B=D, azaz C=0, B=-1/3, A=D=1/3

\int\frac{x+1}{(x^2+x+1)^2}=\frac{1}{3}\frac{x-1}{x^2+x+1}+\int\frac{1}{3}\frac{1}{x^2+x+1}

Területszámításos feladatok

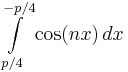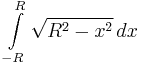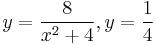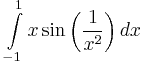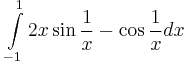
Explicit görbék által határolt területek: 1. \int\limits_{p/4}^{-p/4} \cos (nx)\,dx, 2. \int\limits_{-R}^{R}\sqrt{R^2-x^2}\,dx, 3. y=\frac{8}{x^2+4}, y=\frac{1}{4} által határolt síktartomány területe, 4. f(x)=\sqrt[3]{x}, g(x)=x^3, a) síktartomány területe, bezárt előjeles terület, 5. \int\limits_{-1}^{1}x\sin\left(\frac{1}{x^2}\right)dx, 6. \int\limits_{-1}^{1}2x\sin\frac{1}{x}-\cos\frac{1}{x}dx

Implicit görbék által határolt területek: 7. y2 − 2x − 4y + 6 = 0, y = − x + 3,

Paraméteres megadású görbék, terület és szektortartomány területe:

T=\int\limits_{x_1}^{x_2}f(x)dx=\int\limits_{t_1}^{t_2}y(t)\dot{x}(t)dt
T=\int\limits_{\varphi_1}^{\varphi_2}\frac{1}{2}r^2(\varphi)d\varphi
T=\frac{1}{2}\int\limits_{t_1}^{t_2}\dot{y}(t)x(t)-y(t)\dot{x}(t)dt

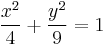8. \frac{x^2}{4}+\frac{y^2}{9}=1, x=0, y=0

9. parabolikus spirál: 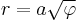r=a\sqrt{\varphi}

3. gyakorlat

Az integrál alkalmazásai

[1]

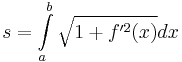
1) Ívhossz: s=\int\limits_a^b\sqrt{1+f'^2(x)}dx

f(x) = x2 [0,1]

2) Forgástest térfogata:

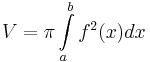
V=\pi\int\limits_a^bf^2(x) dx

f(x) = e − x [0,∞]

3) Forgástest palástfelszíne:

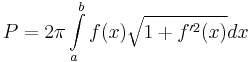
P=2\pi\int\limits_a^bf(x)\sqrt{1+f'^2(x)} dx

f(x)=\sqrt{x}

Az improprius integrál

1) Integrál nem korlátos intervallumon:

(13.29) \int\limits_1^\infty \frac{1}{x\ln^2 x}\,\mathrm{d}x=\int\limits_2^\infty \frac{1}{x}\ln^{-2} x \,\mathrm{d}x= \left[\frac{\ln^{-1} x}{-1}\right]_2^{\infty}=0-(-\frac{1}{\ln 2})=\frac{1}{\ln 2}

2) Nem korlátos függvény integrálja:

(13.38) \int\limits_1^3 \frac{1}{\sqrt[3]{(x-1)^2}}\,\mathrm{d}x=\int\limits_1^3(x-1)^{-2/3} \,\mathrm{d}x= \left[3\sqrt[3]{x-1}\right]_1^{3}=3\sqrt[3]{3}

(13.41) \int\limits_0^2 \frac{1}{\sqrt[3]{(x-1)^2}}\,\mathrm{d}x=

pr. fv.: 3\sqrt[3]{x-1}

\int\limits_0^2(x-1)^{-2/3} \,\mathrm{d}x= \left[3\sqrt[3]{x-1}\right]_0^{1}+\left[3\sqrt[3]{x-1}\right]_1^{2}=6

3) Riemann-integrálható, impropriusan integrállal kiszámítható integrálok:

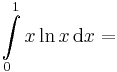
\int\limits_0^1 x\ln x\,\mathrm{d}x=

pr. fv.: 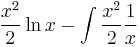\frac{x^2}{2}\ln x-\int\frac{x^2}{2}\frac{1}{x}

\int\limits_0^1 x\ln x\,\mathrm{d}x=\left[\frac{x^2}{2}\ln x-\frac{x^2}{4}\right]_0^1=0-\frac{1}{4}-(0-0)=-\frac{1}{4}

Lineáris algebra, alapfogalmak

1. Legyen V a legfeljebb 2.foku, valos egyutthatos polinomok halmaza. Igazoljuk, hogy V a szokasos muveletekkel vektorteret alkot (nem kell minden vektorter-axiomat ellenorizni, eleg, ha vilagos nekik, hogy miket kene ellenorizni, es mondjuk 1-2 axiomat tenyleg reszletesen ellenoriztek is).

2. Igazoljuk, hogy V (itt V az elobbi) izomorf R^3-al (azaz a 3 hosszu szamsorozatok vektorterevel). Jegyezzetek meg, hogy mivel R^3 vektorter, ezert az izomorfiabol is kovetkezik, hogy V is vektorter.

3. Legyen f: V --> R (itt V az elobbi), f(p) = p(2) (behelyettesites). Igazoljuk, hogy f linearis lekepezes.

4. Legyen W a tervektorok halmaza, f: W --> W egy elore rogzitett, origon atmeno sikra vonatkozo meroleges vetites. Jo alaposan ellenorizzetek, hogy f linearis lekepezes. Beszeljetek meg veluk, mi van akkor, ha az origo nincs benne az elore rogzitett sikban ? A megfelelo f akkor is linearis marad ?

5. Legyen F a folytonos fuggvenyek halmaza. Igazoljuk, hogy a szokasos muveletekkel ez is vektorter. Mi lesz az {1, 2x, 1-x^2} fuggvenyek altal generalt alter ? (Itt 1 a konstans-1 fv, es - a rossz gyakorlatot kovetve - x az identitas-fv akar lenni).

6. Az elobbi F-nek altere-e a paros fuggvenyek, illetve a paratlan fuggvenyek halmaza ?

7. Eloall-e az elobbi F-ben az x^3 fuggveny x^2 es cos(x) linearis kombinaciojakent ? (Tipp: nem, mert x^3 nem paros, mig x^2 es cos(x) benne van a paros fuggvenyek altereben).

8. Legyen V a tervektorok halmaza, legyen a egy rogzitett vektor, es legyen f: V --> V, f(v) = v x a (azaz f(v) = "v es a vektorialis szorzata"). Igazoljuk, hogy f linearis.

9. Legyen W a 4 hosszu szamsorozatok vektortere. Eloall-e a megadott vektor a megadott vektorrendszer lin. kombinaciojakent ? Ha igen, hogyan, ha nem, akkor miert nem...

(a) (3,3,4,5) {(1,2,3,4), (2,2,2,2), (1,0,0,0)}, (b) (3,3,4,5) {(1,2,3,4), (1,0,0,0)}, (c) (-4,-2,0,2) {1,2,3,4), (2,2,2,2)}, (d) (3,1,-7,5) {(1,0,0,0), (0,1,0,0), (0,0,1,0), (0,0,0,1) }.

A lap eredeti címe: „http://wiki.math.bme.hu/index.php?title=Matematika_k%C3%B6zlek_A2a_2014&oldid=9799”
Személyes eszközök