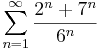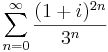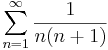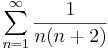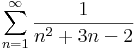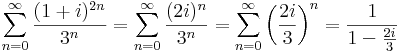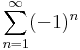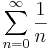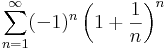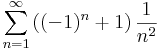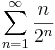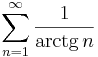Matematika közlek a3 2010 1. gyakorlat
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) (→Numerikus sorok) |
Mozo (vitalap | szerkesztései) (→Numerikus sorok) |
||
| 8. sor: | 8. sor: | ||
# <math>\sum\limits_{n=1}^{\infty}\frac{1}{n(n+2)}</math> | # <math>\sum\limits_{n=1}^{\infty}\frac{1}{n(n+2)}</math> | ||
# <math>\sum\limits_{n=1}^{\infty}\frac{1}{n^2+3n-2}</math> | # <math>\sum\limits_{n=1}^{\infty}\frac{1}{n^2+3n-2}</math> | ||
| + | |||
| + | ''Mo.'' | ||
| + | |||
| + | :<math>\sum\limits_{n=0}^{\infty}\frac{(1+i)^{2n}}{3^n}=\sum\limits_{n=0}^{\infty}\frac{(2i)^{n}}{3^n}=\sum\limits_{n=0}^{\infty}\left(\frac{2i}{3}\right)^n=\frac{1}{1-\frac{2i}{3}}</math> | ||
'''2.''' Cauchy-kritérium, integrálkritérium, szükséges feltétel | '''2.''' Cauchy-kritérium, integrálkritérium, szükséges feltétel | ||
A lap 2010. szeptember 6., 09:22-kori változata
Numerikus sorok
1. Számítsuk ki a következő sorok összegét (ha létezik)!
Mo.
2. Cauchy-kritérium, integrálkritérium, szükséges feltétel