Matematika közlek a3 2010 1. gyakorlat
Mozo (vitalap | szerkesztései) (→Numerikus sorok) |
Mozo (vitalap | szerkesztései) |
||
| (egy szerkesztő 12 közbeeső változata nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
| − | ==Numerikus | + | ==Numerikus sor definíciója== |
| + | |||
| + | :<math>(a_n):\mathbf{N}\to \mathbf{R}</math> vagy <math>\mathbf{N}\to \mathbf{C}</math> sorozat, akkor ennek részletösszegsorozata: | ||
| + | :<math>(s_n):n\mapsto\sum\limits_{k=1}^n a_k</math> | ||
| + | :<math>(s_n)</math>-t az <math>(a_n)</math> sorozatból képezett '''sor'''nak nevezzük és azt mondjuk, hogy az <math>(s_n)</math> sor konvergens, és összege az | ||
| + | :<math>\sum\limits_{n=1}^{\infty}a_n</math> | ||
| + | szám, ha az <math>(s_n)</math> sorozat konvergens, és határértéke | ||
| + | :<math>\lim\limits_{n\to \infty}s_n=\sum\limits_{n=1}^{\infty}a_n</math> | ||
| + | ''Megjegyzés'' A <math>z_n=x_n+iy_n</math> komplex sorozat konvergens és határértéke a ''z'' komplex szám, ha | ||
| + | minden ε>0 szám esetén létezik N, hogy ha n>N, akkor |z_n-z|<ε. <math>(z_n)</math> konvergens pontosan akkor, ha <math>(x_n)</math> és <math>(y_n)</math> is konvergens, mint valós sorozat. | ||
| + | |||
'''1. ''' Számítsuk ki a következő sorok összegét (ha létezik)! | '''1. ''' Számítsuk ki a következő sorok összegét (ha létezik)! | ||
| 7. sor: | 17. sor: | ||
# <math>\sum\limits_{n=1}^{\infty}\frac{1}{n(n+1)}</math> | # <math>\sum\limits_{n=1}^{\infty}\frac{1}{n(n+1)}</math> | ||
# <math>\sum\limits_{n=1}^{\infty}\frac{1}{n(n+2)}</math> | # <math>\sum\limits_{n=1}^{\infty}\frac{1}{n(n+2)}</math> | ||
| − | # <math>\sum\limits_{n=1}^{\infty}\frac{1}{n^2+ | + | # <math>\sum\limits_{n=1}^{\infty}\frac{1}{n^2+5n+4}</math> (!) |
''Mo.'' | ''Mo.'' | ||
| 13. sor: | 23. sor: | ||
:<math>\sum\limits_{n=0}^{\infty}\frac{(1+i)^{2n}}{3^n}=\sum\limits_{n=0}^{\infty}\frac{(2i)^{n}}{3^n}=\sum\limits_{n=0}^{\infty}\left(\frac{2i}{3}\right)^n=\frac{1}{1-\frac{2i}{3}}</math> | :<math>\sum\limits_{n=0}^{\infty}\frac{(1+i)^{2n}}{3^n}=\sum\limits_{n=0}^{\infty}\frac{(2i)^{n}}{3^n}=\sum\limits_{n=0}^{\infty}\left(\frac{2i}{3}\right)^n=\frac{1}{1-\frac{2i}{3}}</math> | ||
:<math>\sum\limits_{n=1}^{\infty}\frac{1}{n(n+1)}=\sum\limits_{n=1}^{\infty}\frac{1}{n}-\frac{1}{n+1}=\lim\limits_{n\to \infty}1-\frac{1}{n+1}=1</math> | :<math>\sum\limits_{n=1}^{\infty}\frac{1}{n(n+1)}=\sum\limits_{n=1}^{\infty}\frac{1}{n}-\frac{1}{n+1}=\lim\limits_{n\to \infty}1-\frac{1}{n+1}=1</math> | ||
| − | :<math>\sum\limits_{n=1}^{\infty}\frac{1}{n(n+2)}=\sum\limits_{n=1}^{\infty}\frac{1}{2}\left(\frac{1}{n}-\frac{1}{n+2}\right)=\frac{1}{2}\lim\limits_{n\to \infty}1-\frac{1}{n+2}=1/2</math> | + | :<math>\sum\limits_{n=1}^{\infty}\frac{1}{n(n+2)}=\sum\limits_{n=1}^{\infty}\frac{1}{2}\left(\frac{1}{n}-\frac{1}{n+2}\right)=</math> |
| + | :<math>\frac{1}{2}\lim\limits_{n\to \infty}1-\frac{1}{n+2}=\lim\limits_{n\to \infty}\frac{1}{2}\left(1-\frac{1}{3}+\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{5}+\frac{1}{4}-\frac{1}{6}+...\right)=\frac{3}{4}</math> | ||
| + | : <math>\sum\limits_{n=1}^{\infty}\frac{1}{n^2+5n+4}=\sum\limits_{n=1}^{\infty}\frac{1}{(n+1)(n+4)}=\sum\limits_{n=1}^{\infty}\frac{1}{3}\left(\frac{1}{n+1}-\frac{1}{n+4}\right)=...</math> | ||
| − | ''' | + | ==Cauchy-kritérium, integrálkritérium, szükséges feltétel== |
| + | |||
| + | ''Cauchy-kritérium''. Az <math>(a_n)</math>-ből képezett <math>(s_n)</math> konvergens, pontosan akkor, ha minden ε>0-hoz létezik N, hogy minden m>n>N-re | ||
| + | :<math>|s_m-s_n|<\varepsilon</math> | ||
| + | |||
| + | ''Szükséges feltétel''. Ha ∑<math>(a_n)</math> konvergens, akkor <math>(a_n)</math> nullsorozat. | ||
| + | |||
| + | ''Integrálkritérium''. Ha az <math>f:[N,\infty]\to \mathbf{R}</math> monoton csükkenő és pozitív valós függvény, akkor az | ||
| + | :<math>\int\limits_{N}^\infty f(x)\;\mathrm{d}x</math> | ||
| + | impróprius integrál és a | ||
| + | :<math>\sum\limits_{n=N}^\infty f(n)</math> | ||
| + | numerikus sor egyszerre konvergens. | ||
| + | |||
| + | '''2.''' Konvergensek-e az alábbi sorok? | ||
# <math>\sum\limits_{n=1}^{\infty}(-1)^n</math> | # <math>\sum\limits_{n=1}^{\infty}(-1)^n</math> | ||
# <math>\sum\limits_{n=0}^{\infty}\frac{1}{n}</math> | # <math>\sum\limits_{n=0}^{\infty}\frac{1}{n}</math> | ||
# <math>\sum\limits_{n=1}^{\infty}(-1)^n\left(1+\frac{1}{n}\right)^n</math> | # <math>\sum\limits_{n=1}^{\infty}(-1)^n\left(1+\frac{1}{n}\right)^n</math> | ||
| − | # <math>\sum\limits_{n=1}^{\infty}\left((-1)^n+1\right)\frac{1}{n | + | # <math>\sum\limits_{n=1}^{\infty}\left((-1)^n+1\right)\frac{1}{n}</math> |
# <math>\sum\limits_{n=1}^{\infty}\frac{n}{2^n}</math> | # <math>\sum\limits_{n=1}^{\infty}\frac{n}{2^n}</math> | ||
# <math>\sum\limits_{n=1}^{\infty}\frac{1}{\mathrm{arctg}\,n}</math> | # <math>\sum\limits_{n=1}^{\infty}\frac{1}{\mathrm{arctg}\,n}</math> | ||
| − | ''Mo.'' | + | ''Mo.'' |
| − | < | + | |
| + | :<math>\sum\limits_{n=0}^{\infty}\frac{1}{n}</math> | ||
| + | legyen ε=1, N tetszőleges, m=2N, n=N. Ekkor | ||
| + | :<math>|s_m-s_n|=\sum\limits_{k=0}^{N-1}\frac{1}{N+k}\leq \sum\limits_{k=0}^{N-1}\frac{1}{N}=1</math> | ||
| + | Intergálkritériummal: | ||
| + | :<math>\int\limits_{0}^{\infty} xe^{-x}\;\mathrm{d}x=[x(-e^{-x})]_0^\infty-\int\limits_{0}^\infty-e^{-x}\;\mathrm{d}x=0+[e^{-x}]_0^\infty=1</math> | ||
A lap jelenlegi, 2010. szeptember 15., 09:31-kori változata
Numerikus sor definíciója
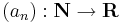 vagy
vagy 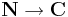 sorozat, akkor ennek részletösszegsorozata:
sorozat, akkor ennek részletösszegsorozata:
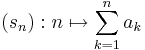
- (sn)-t az (an) sorozatból képezett sornak nevezzük és azt mondjuk, hogy az (sn) sor konvergens, és összege az
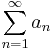
szám, ha az (sn) sorozat konvergens, és határértéke
Megjegyzés A zn = xn + iyn komplex sorozat konvergens és határértéke a z komplex szám, ha minden ε>0 szám esetén létezik N, hogy ha n>N, akkor |z_n-z|<ε. (zn) konvergens pontosan akkor, ha (xn) és (yn) is konvergens, mint valós sorozat.
1. Számítsuk ki a következő sorok összegét (ha létezik)!
-
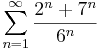
-
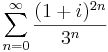
-
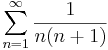
-
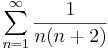
-
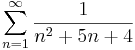 (!)
(!)
Mo.
Cauchy-kritérium, integrálkritérium, szükséges feltétel
Cauchy-kritérium. Az (an)-ből képezett (sn) konvergens, pontosan akkor, ha minden ε>0-hoz létezik N, hogy minden m>n>N-re
Szükséges feltétel. Ha ∑(an) konvergens, akkor (an) nullsorozat.
Integrálkritérium. Ha az ![f:[N,\infty]\to \mathbf{R}](/upload/math/6/a/3/6a3e45510f192101c8e1daf997f7228c.png) monoton csükkenő és pozitív valós függvény, akkor az
monoton csükkenő és pozitív valós függvény, akkor az
impróprius integrál és a
numerikus sor egyszerre konvergens.
2. Konvergensek-e az alábbi sorok?
Mo.
legyen ε=1, N tetszőleges, m=2N, n=N. Ekkor
Intergálkritériummal:
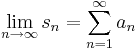
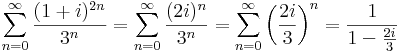
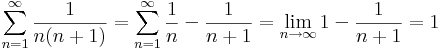
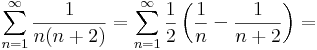
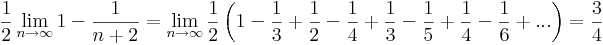
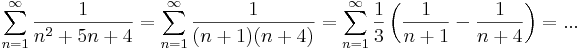
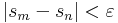
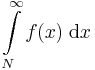
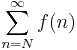
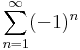
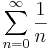
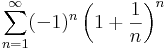
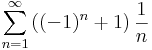
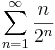
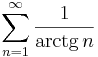
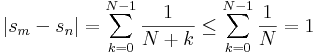
![\int\limits_{0}^{\infty} xe^{-x}\;\mathrm{d}x=[x(-e^{-x})]_0^\infty-\int\limits_{0}^\infty-e^{-x}\;\mathrm{d}x=0+[e^{-x}]_0^\infty=1](/upload/math/f/e/2/fe20f1cc0fb0fec57ff0820315217416.png)