Matematika közlek a3 2010 1. gyakorlat
A MathWikiből
A lap korábbi változatát látod, amilyen Mozo (vitalap | szerkesztései) 2010. szeptember 6., 18:22-kor történt szerkesztése után volt.
Numerikus sorok
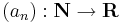 vagy
vagy 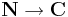 sorozat, akkor ennek részletösszegsorozata:
sorozat, akkor ennek részletösszegsorozata:
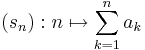
- (sn)-t az (an) sorozatból képezett sornak nevezzük és azt mondjuk, hogy az (sn) sor konvergens, és összege az
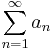
szám, ha az (sn) sorozat konvergens, és határértéke
Megjegyzés A zn = xn + iyn komplex sorozat konvergens és határértéke a z komplex szám, ha minden ε>0 szám esetén létezik N, hogy ha n>N, akkor |z_n-z|<ε. (zn) konvergens pontosan akkor, ha (xn) és (yn) is konvergens, mint valós sorozat.
1. Számítsuk ki a következő sorok összegét (ha létezik)!
Mo.
2. Cauchy-kritérium, integrálkritérium, szükséges feltétel
Mo.
legyen ε=1, N tetszőleges, m=2N, n=N. Ekkor
Intergálkritériummal:
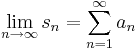
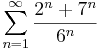
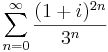
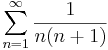
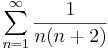
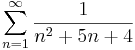
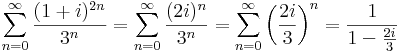
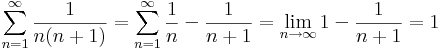
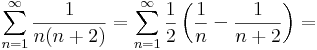
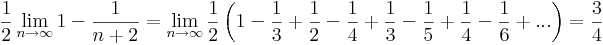
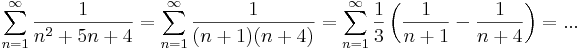
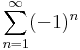
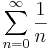
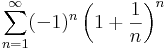
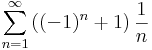
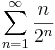
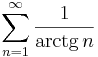
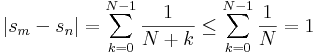
![\int\limits_{0}^{\infty} xe^{-x}\;\mathrm{d}x=[x(-e^{-x})]_0^\infty-\int\limits_{0}^\infty-e^{-x}\;\mathrm{d}x=0+[e^{-x}]_0^\infty=1](/upload/math/f/e/2/fe20f1cc0fb0fec57ff0820315217416.png)