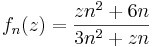Matematika közlek a3 2010 2. gyakorlat
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) (→Majoráns-, hányados-, gyök- és Leibniz-kritérium) |
Mozo (vitalap | szerkesztései) (→Majoráns-, hányados-, gyök- és Leibniz-kritérium) |
||
| 2. sor: | 2. sor: | ||
''Majoráns-kritérium'' -- Legyen <math>(a_n)</math> és <math>(b_n)</math> olyan, hogy egy indextől kezdődően <math>|a_n|\leq |b_n|</math> és ∑<math>(b_n)</math> konvergens. Ekkor ∑<math>(a_n)</math> is konvergens (és ∑<math>(b_n)</math> a majoráns sora). | ''Majoráns-kritérium'' -- Legyen <math>(a_n)</math> és <math>(b_n)</math> olyan, hogy egy indextől kezdődően <math>|a_n|\leq |b_n|</math> és ∑<math>(b_n)</math> konvergens. Ekkor ∑<math>(a_n)</math> is konvergens (és ∑<math>(b_n)</math> a majoráns sora). | ||
| − | ''Hányados-kritérium'' -- Legyen (a_n) olyan, hogy létezik a <math>\lim\limits_{n\to \infty}\left|\frac{a_{n+1}}{a_n}\right|.</math> | + | ''Hányados-kritérium'' -- Legyen <math>(a_n)</math> olyan, hogy létezik a <math>\lim\limits_{n\to \infty}\left|\frac{a_{n+1}}{a_n}\right|.</math> |
# ha <math>\lim\limits_{n\to \infty}\left|\frac{a_{n+1}}{a_n}\right|< 1</math>, akkor ∑<math>(a_n)</math> konvergens és | # ha <math>\lim\limits_{n\to \infty}\left|\frac{a_{n+1}}{a_n}\right|< 1</math>, akkor ∑<math>(a_n)</math> konvergens és | ||
| + | # ha <math>\lim\limits_{n\to \infty}\left|\frac{a_{n+1}}{a_n}\right|> 1</math>, akkor ∑<math>(a_n)</math> divergens. | ||
| + | |||
| + | ''Gyök-kritérium'' -- Legyen <math>(a_n)</math> olyan, hogy létezik a <math>\lim\limits_{n\to \infty}\sqrt[n]{|a_n|}.</math> | ||
| + | # ha <math>\lim\limits_{n\to \infty}\sqrt[n]{|a_n|}< 1</math>, akkor ∑<math>(a_n)</math> konvergens és | ||
| + | # ha <math>\lim\limits_{n\to \infty}\sqrt[n]{|a_n|}> 1</math>, akkor ∑<math>(a_n)</math> divergens. | ||
| + | |||
| + | ''Leibniz-kritérium'' -- Ha <math>|a_n|</math> monoton csökkenő módon tart a 0-hoz, akkor <math>\sum((-1)^n a_n)</math> konvergens. | ||
| + | |||
'''1.''' | '''1.''' | ||
A lap 2010. szeptember 15., 09:41-kori változata
Majoráns-, hányados-, gyök- és Leibniz-kritérium
Majoráns-kritérium -- Legyen (an) és (bn) olyan, hogy egy indextől kezdődően 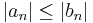 és ∑(bn) konvergens. Ekkor ∑(an) is konvergens (és ∑(bn) a majoráns sora).
és ∑(bn) konvergens. Ekkor ∑(an) is konvergens (és ∑(bn) a majoráns sora).
Hányados-kritérium -- Legyen (an) olyan, hogy létezik a 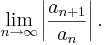
- ha
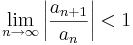 , akkor ∑(an) konvergens és
, akkor ∑(an) konvergens és
- ha
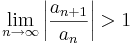 , akkor ∑(an) divergens.
, akkor ∑(an) divergens.
Gyök-kritérium -- Legyen (an) olyan, hogy létezik a ![\lim\limits_{n\to \infty}\sqrt[n]{|a_n|}.](/upload/math/9/6/f/96f8baafbfbcfc9a5d666995ddc70617.png)
- ha
![\lim\limits_{n\to \infty}\sqrt[n]{|a_n|}< 1](/upload/math/f/b/a/fba4f50f584d88332f6fe65498343be8.png) , akkor ∑(an) konvergens és
, akkor ∑(an) konvergens és
- ha
![\lim\limits_{n\to \infty}\sqrt[n]{|a_n|}> 1](/upload/math/0/5/6/05623bb475cb22817806a081fcdf54cc.png) , akkor ∑(an) divergens.
, akkor ∑(an) divergens.
Leibniz-kritérium -- Ha | an | monoton csökkenő módon tart a 0-hoz, akkor 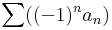 konvergens.
konvergens.
1.
Mo.
Függvénysorozatok
Az azonos A ⊆ C halmazon értelmezett komplex vagy valós függvények 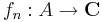 sorozatának konvergenciatartományán azzon K halmazt értjük, melyhez pontosan akkor tartozik az x pont, ha az (fn(x)) sorozat konvergens.
sorozatának konvergenciatartományán azzon K halmazt értjük, melyhez pontosan akkor tartozik az x pont, ha az (fn(x)) sorozat konvergens.
4. Függvénysorozatok pontonkénti konvergenciája
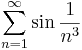
![\sum\limits_{n=1}^{\infty}\frac{1}{\sqrt[n]{\ln n}}](/upload/math/e/8/7/e87aa018482b16536f1a5356ca91d73c.png)