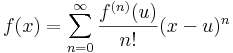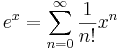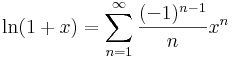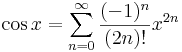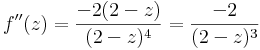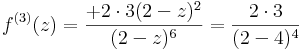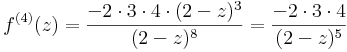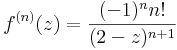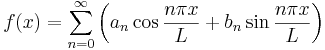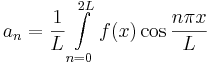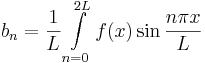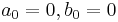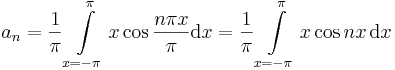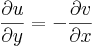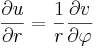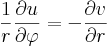Matematika közlek a3 2010 3. gyakorlat

A MathWikiből
(Változatok közti eltérés)
 
1. sor: 1. sor:
 
==Taylor-sor==
 
==Taylor-sor==
−
Sorbafejthető
+
Sorbafejthető (analitikus) függvény esetén a függvény előáll a következő sor alakjában:
−
(analitikus) függvény esetén a függvény előáll a következő sor  
+
−
alakjában:
+
 
:<math>f(x)=\sum\limits_{n=0}^{\infty}\frac{f^{(n)}(u)}{n!}(x-u)^n</math>
 
:<math>f(x)=\sum\limits_{n=0}^{\infty}\frac{f^{(n)}(u)}{n!}(x-u)^n</math>
−
Nevezetes
+
Nevezetes sorok:
−
sorok:
+
 
:<math>e^x=\sum\limits_{n=0}^\infty\frac{1}{n!}x^n</math>
 
:<math>e^x=\sum\limits_{n=0}^\infty\frac{1}{n!}x^n</math>
 
:<math>\mathrm{ln}(1+x)=\sum\limits_{n=1}^\infty\frac{(-1)^{n-1}}{n}x^n</math>
 
:<math>\mathrm{ln}(1+x)=\sum\limits_{n=1}^\infty\frac{(-1)^{n-1}}{n}x^n</math>
14. sor: 11. sor:
 
'''1. Feladat.''' ''u=0''
 
'''1. Feladat.''' ''u=0''
 
:a) <math>f(z)=\frac{z}{2-z}</math>
 
:a) <math>f(z)=\frac{z}{2-z}</math>
−
:b) <math>f(z)=z^4-2z^3+2</math>, ''u=1''.
+
:b) <math>f(z)=z^4-2z^3+2\,</math>, ''u=1''.
−
:c) f(z)=\mathrm{ch}(z):=\frac{e^z+e^{-z}}{2}
+
:c) <math>f(z)=\mathrm{ch}(z):=\frac{e^z+e^{-z}}{2}</math>
  
 
''Mo.''  
 
''Mo.''  
29. sor: 26. sor:
 
így a Taylor-sor:
 
így a Taylor-sor:
 
<math>\sum\limits_{n=0}^{\infty}\frac{(-1)^n}{2^{n+1}}</math>
 
<math>\sum\limits_{n=0}^{\infty}\frac{(-1)^n}{2^{n+1}}</math>
−
:b)
+
:b)<math>f(z)=z^4-2z^3+2\,</math>
−
<math>f(z)=z^4-2z^3+2</math>
+
:<math>f'(z)=4z^3-2\cdot 3z^2\,</math> ---- 2
−
:<math>f'(z)=4z^3-2\cdot 3z^2</math> ---- 2
+
 
:<math>f''(z)=4\cdot 3 z^2-2\cdot 2\cdot 3z</math> ----
 
:<math>f''(z)=4\cdot 3 z^2-2\cdot 2\cdot 3z</math> ----
 
:<math>f^{(4)}(z)=4\cdot 3\cdot 2 z-2\cdot 2\cdot 3</math>
 
:<math>f^{(4)}(z)=4\cdot 3\cdot 2 z-2\cdot 2\cdot 3</math>
37. sor: 33. sor:
 
==Fourier-sor==
 
==Fourier-sor==
  
−
:<math>f(x)=\sum\limits_{n=0}^infty\left(a_n\cos\frac{n\pi  
+
:<math>f(x)=\sum\limits_{n=0}^\infty\left(a_n\cos\frac{n\pi  
−
x}{L}\right+b_n\sin\frac{n\pi x}{L})</math>
+
x}{L}+b_n\sin\frac{n\pi x}{L}\right)</math>
−
ahol: a<sub>0</sub>="átlag", b<sub>0</sub>=0,  
+
ahol: a<sub>0</sub>="átlag", b<sub>0</sub>=0, L="félperiódus"
−
L="félperiódus"
+
 
:<math>a_n=\frac{1}{L}\int\limits_{n=0}^{2L}f(x)\cos\frac{n\pi  
 
:<math>a_n=\frac{1}{L}\int\limits_{n=0}^{2L}f(x)\cos\frac{n\pi  
 
x}{L}</math>
 
x}{L}</math>
51. sor: 46. sor:
  
 
''Mo.''
 
''Mo.''
−
:<math>a_0=0, b_0=0</math>
+
:<math>a_0=0, b_0=0\,</math>
 
:<math>a_n=\frac{1}{\pi}\int\limits_{x=-\pi}^\pi x\cos\frac{n\pi  
 
:<math>a_n=\frac{1}{\pi}\int\limits_{x=-\pi}^\pi x\cos\frac{n\pi  
 
x}{\pi}\mathrm{d}x=\frac{1}{\pi}\int\limits_{x=-\pi}^\pi x\cos  
 
x}{\pi}\mathrm{d}x=\frac{1}{\pi}\int\limits_{x=-\pi}^\pi x\cos  
75. sor: 70. sor:
 
'''3. Feladat.''' Hol diffható és mi a deriváltja?  
 
'''3. Feladat.''' Hol diffható és mi a deriváltja?  
 
:a) <math>f(z)=z\overline{z}</math>
 
:a) <math>f(z)=z\overline{z}</math>
−
:b) <math>f(z)=ln x</math>
+
:b) <math>f(z)=ln x\,</math>
 
''Mo.''  
 
''Mo.''  
 
:a) <math>f(x,y)=(x+iy)(y-iy)=x^2+y^2+0.i</math>
 
:a) <math>f(x,y)=(x+iy)(y-iy)=x^2+y^2+0.i</math>

A lap 2010. szeptember 20., 16:23-kori változata

Taylor-sor

Sorbafejthető (analitikus) függvény esetén a függvény előáll a következő sor alakjában:

f(x)=\sum\limits_{n=0}^{\infty}\frac{f^{(n)}(u)}{n!}(x-u)^n

Nevezetes sorok:

e^x=\sum\limits_{n=0}^\infty\frac{1}{n!}x^n
\mathrm{ln}(1+x)=\sum\limits_{n=1}^\infty\frac{(-1)^{n-1}}{n}x^n
\sin x=\sum\limits_{n=0}^\infty\frac{(-1)^n}{(2n+1)!}x^{2n+1}
\cos x=\sum\limits_{n=0}^\infty\frac{(-1)^n}{(2n)!}x^{2n}

1. Feladat. u=0

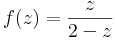
a) f(z)=\frac{z}{2-z}
b) 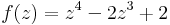f(z)=z^4-2z^3+2\,, u=1.
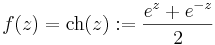
c) f(z)=\mathrm{ch}(z):=\frac{e^z+e^{-z}}{2}

Mo.

a)

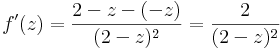
f'(z)=\frac{2-z-(-z)}{(2-z)^2}=\frac{2}{(2-z)^2}

f''(z)= \frac{-2(2-z)}{(2-z)^4}=\frac{-2}{(2-z)^3}
f^{(3)}(z)= \frac{+2\cdot 3(2-z)^2}{(2-z)^6}=\frac{2\cdot 3}{(2-4)^4}
f^{(4)}(z)= \frac{-2\cdot 3\cdot 4\cdot (2-z)^3}{(2-z)^8}=\frac{-2\cdot 3\cdot 4}{(2-z)^5}
f^{(n)}(z)=\frac{(-1)^n n!}{(2-z)^{n+1}}

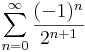
így a Taylor-sor: \sum\limits_{n=0}^{\infty}\frac{(-1)^n}{2^{n+1}}

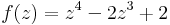
b)f(z)=z^4-2z^3+2\,
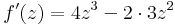f'(z)=4z^3-2\cdot 3z^2\, ---- 2
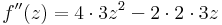f''(z)=4\cdot 3 z^2-2\cdot 2\cdot 3z ----
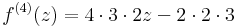
f^{(4)}(z)=4\cdot 3\cdot 2 z-2\cdot 2\cdot 3
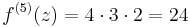
f^{(5)}(z)=4\cdot 3\cdot 2 =24

Fourier-sor

f(x)=\sum\limits_{n=0}^\infty\left(a_n\cos\frac{n\pi x}{L}+b_n\sin\frac{n\pi x}{L}\right)

ahol: a0="átlag", b0=0, L="félperiódus"

a_n=\frac{1}{L}\int\limits_{n=0}^{2L}f(x)\cos\frac{n\pi x}{L}
b_n=\frac{1}{L}\int\limits_{n=0}^{2L}f(x)\sin\frac{n \pi x}{L}

2. Feladat.

f(x)=x (-π,\pi]

Mo.

a_0=0, b_0=0\,
a_n=\frac{1}{\pi}\int\limits_{x=-\pi}^\pi x\cos\frac{n\pi x}{\pi}\mathrm{d}x=\frac{1}{\pi}\int\limits_{x=-\pi}^\pi x\cos nx\,\mathrm{d}x

...

Komplex differenciálhatóság

Cauchy--Riemann-egyenletek:

\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}
\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}

Polárkoordinátákban:


\frac{\partial u}{\partial r}=\frac{1}{r}\frac{\partial v}{\partial \varphi}
\frac{1}{r}\frac{\partial u}{\partial \varphi}=-\frac{\partial v}{\partial r}

3. Feladat. Hol diffható és mi a deriváltja?

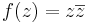
a) f(z)=z\overline{z}
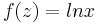
b) f(z)=ln x\,

Mo.

a) f(x,y) = (x + iy)(y − iy) = x2 + y2 + 0.i
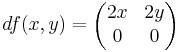
df(x,y)=\begin{pmatrix}2x & 2y \\ 0 & 0\end{pmatrix}

Tehát csak a (0,0)-ban teljesül C--R. Itt a definíció szerint látjuk be:

Értelmezés sikertelen (PNG-vé alakítás sikertelen; ellenőrizd, hogy a latex és dvipng (vagy dvips + gs + convert) helyesen van-e telepítve): lim\limits_{z\to 0}\frac{z\overline{z}}{z}=\lim\limits_{z\to 0}
b)

polárkoordinátás alakban:

\mathrm{ln}(z)=\mathrm{ln}r+i\varphi+ik\pi
A lap eredeti címe: „http://wiki.math.bme.hu/index.php?title=Matematika_k%C3%B6zlek_a3_2010_3._gyakorlat&oldid=6355”
Személyes eszközök