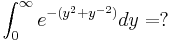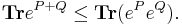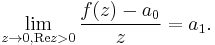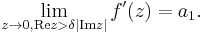Matematika verseny/2011
(→6. feladat) |
(→8. feladat) |
||
| 71. sor: | 71. sor: | ||
b. <math> 1/k! </math> valószínűséggel lesznek | b. <math> 1/k! </math> valószínűséggel lesznek | ||
az <math> 1, 2, \dots, k </math> számok csupa különböző ciklusban. | az <math> 1, 2, \dots, k </math> számok csupa különböző ciklusban. | ||
| + | |||
| + | === A szerkesztő megjegyzése === | ||
| + | |||
| + | A feladatra van olyan megoldás, ami az a. és b. részt is megoldja, de olyan megoldás is, ami csak az a. részt oldja meg. | ||
== 9. feladat == | == 9. feladat == | ||
A lap 2013. április 10., 13:32-kori változata
== Matematika verseny 2011 ==
A 2011. évi BME Matematika versenyt 2011. április 14-én rendezték meg. A verseny általános leírását lásd a Matematika verseny lapon, a feladatsort és eredményeket Horváth Miklós honlapján].
Ez a lap a feladatokat tartalmazza, de ide (vagy allapokra) lehet írni a feladatok megoldását vagy megjegyzéseket hozzájuk.
Tartalomjegyzék |
1. feladat
Adott a,b,c,d oldalhosszúságú síkbeli négyszögek közül melyik lesz maximális területű? Az oldalak ebben a sorrendben csatlakoznak.
2. feladat
Melyek azok a tízes számrendszerben felírt természetes számok, melyek utolsó számjegyét az elejére áthelyezve az eredeti szám 2/3-át kapjuk?
3. feladat
Legyen A invertálható 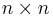 -es mátrix.
Tegyük fel, hogy az A és A − 1 mátrixok minden el
eme nemnegatív.
Bizonyítsuk be, hogy van olyan k > 0 egész,
hogy Ak diagonális mátrix.
-es mátrix.
Tegyük fel, hogy az A és A − 1 mátrixok minden el
eme nemnegatív.
Bizonyítsuk be, hogy van olyan k > 0 egész,
hogy Ak diagonális mátrix.
4. feladat
5. feladat
a. Legyenek  egységvektorok egy euklideszi térben,
egységvektorok egy euklideszi térben,
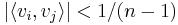 , ha
, ha 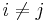 .
Mutassuk meg, hogy
.
Mutassuk meg, hogy  lineárisan függetlenek.
lineárisan függetlenek.
b. Lengyen m = (n − 1)n / 2 + 1,  egységvektorok,
egységvektorok,
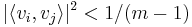 , ha
, ha 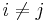 .
Mutassuk meg, hogy
.
Mutassuk meg, hogy  közül kiválasztható n lineárisan független vektor.
közül kiválasztható n lineárisan független vektor.
6. feladat
Az irányított G egyszerű gráf irányított kromatikus száma, χi(G)
az a legkisebb k,
amelyre k színnel színezhetők a csúcsok úgy,
hogy egy él két vége különböző színű
és bármely adott színpárban csak az egyik irányba vezethet él.
Mutassuk meg, hogy nincs olyan 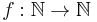 függvény,
melyre
függvény,
melyre 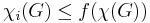 teljesül minden G-re,
ahol χ(G) a megfelelő irányítatlan gráf kromatikus száma.
Azaz az irányított kromatikus szám nem becsülhető a kromatikus szám ismeretében.
teljesül minden G-re,
ahol χ(G) a megfelelő irányítatlan gráf kromatikus száma.
Azaz az irányított kromatikus szám nem becsülhető a kromatikus szám ismeretében.
A szerkesztő megjegyzése
A feladatot értsük úgy, hogy csak olyan G gráfokat tekintünk, amelyekben semelyik két csúcs között nincs oda-vissza él (így az irányított kromatikus szám mindig véges).
7. feladat
Mutassuk meg, hogy ha 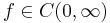 és minden x > 0-ra
és minden x > 0-ra 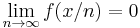 ,
akkor
,
akkor 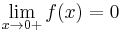 .
.
8. feladat
Legyen 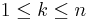 .
Mutassuk meg, hogy az
.
Mutassuk meg, hogy az 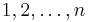 számok egy véletlen permutációjánál
számok egy véletlen permutációjánál
a. 1 / k valószínűséggel lesznek
az 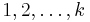 számok ugyanabban a ciklusban,
számok ugyanabban a ciklusban,
b. 1 / k! valószínűséggel lesznek
az 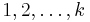 számok csupa különböző ciklusban.
számok csupa különböző ciklusban.
A szerkesztő megjegyzése
A feladatra van olyan megoldás, ami az a. és b. részt is megoldja, de olyan megoldás is, ami csak az a. részt oldja meg.
9. feladat
Legyenek P,Q ortogonális projekciók egy véges dimenziós térben. Mutassuk meg, hogy
10. feladat
Legyen f(z) reguláris a Rez > 0 félsíkon. Tegyük fel, hogy
Bizonyítsuk be, hogy tetszőleges δ > 0 esetén