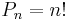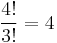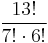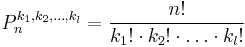Matematikai előismeretek 3.

A MathWikiből
(Változatok közti eltérés)
(→Permutáció)
(→Megoldások)
 
(egy szerkesztő 10 közbeeső változata nincs mutatva)
15. sor: 15. sor:
 
'''1.''' Anna, Gabó, Réka és Petra együtt mennek egyetemre. Hányféle sorrendben léphetik át az egyetem küszöbét, ha mind külön lépnek be?
 
'''1.''' Anna, Gabó, Réka és Petra együtt mennek egyetemre. Hányféle sorrendben léphetik át az egyetem küszöbét, ha mind külön lépnek be?
  
−
'''2.''' Hány különböző ötjegyű szám alkotható a páratlan számjegyekből?
+
'''2.''' Hány különböző ötjegyű szám alkotható a páratlan számjegyekből, ha mindegyik helyiértéken különböző számjegy áll?
  
−
'''3.''' Hány különböző ötjegyű szám alkotható a páros számjegyekből?
+
'''3.''' Hány különböző ötjegyű szám alkotható a páros számjegyekből, ha mindegyik helyiértéken különböző számjegy áll?
  
−
'''4.''' Kiteszünk az asztalra sorban négy üveget: Fanta, Sprite, Cherry Coke, Traubiszóda. Hányféle sorrendben rakhatjuk őket sorba? Hányféle sorrendben rakhatjuk őket sorba, ha a Coca Cola termékeket ugyanolyannak vesszük?
+
'''4.''' Kiteszünk az asztalra sorban négy üveget: Fanta, Sprite, Cherry Coke, Traubiszóda. a) Hányféle sorrendben rakhatjuk őket sorba? b) Hányféle sorrendben rakhatjuk őket sorba, ha a Coca Cola termékeket ugyanolyannak vesszük?
  
 
'''5.''' Hányféleképpen állíthatunk sorba 7 fő 12. A-st és 6 fő 12. B-st, ha a sorrendben csak az számít, hogy melyik osztályban vannak, de az nem, hogy kik ők.
 
'''5.''' Hányféleképpen állíthatunk sorba 7 fő 12. A-st és 6 fő 12. B-st, ha a sorrendben csak az számít, hogy melyik osztályban vannak, de az nem, hogy kik ők.
30. sor: 30. sor:
 
   
 
   
 
'''9.''' Egy öt csúcspontú teljes gráf minden csúcsát beszámozzuk. Hány különböző csúcsokból álló háromszöget színezhetünk ki benne?
 
'''9.''' Egy öt csúcspontú teljes gráf minden csúcsát beszámozzuk. Hány különböző csúcsokból álló háromszöget színezhetünk ki benne?
 +
 +
==Megoldások==
 +
 +
'''1.''' Ez 4 elem összes permutációinak száma: 4!. Vagy először 4 lány közül választhatunk, majd 3, 2, és 1. Ezek egymástól független választások, ezért össze kell szoroznunk őket: <math>4\cdot 3\cdot 2\cdot 1</math>.
 +
 +
'''2.''' 5 páratlan számjegy van: 1, 3, 5, 7, 9, ezek összes permutációinak száma a kérdés: ez 5!.
 +
 +
'''3.''' 5 páros számjegy van: 0, 2, 4, 6, 8. Ezekből készítünk ötjegyű számokat. Ezek nem kezdődhetnek 0-val, ezért az első számjegy lehet
 +
 +
'''4.''' a) Ez 4 elem összes permutációinak száma: 4!. b) Ha a C.C. termékek ugyanolyannak minősülnek (jelöljük őket C-vel, a Traubiszódát
 +
T-vel) akkor négy különböző sorozat lehetséges: TCCC, CTCC, CCTC, CCCT. Vagy, ha 4 elemet sorba rendezünk, akkor ezt 4!-féleképpen lehet megtenni. De akkor vannak esetek, amiket többször számoltunk, mert pl. a TFSC és a TFCS esetek ugyanannak minősülnek. Tehát minden esetet az F, C, S minden sorrendje ugyanannak minősül, ez 3!. Ennyiszerese az eredménynek az a) eset megoldása, tehát, ha ezeket az eseteket nem számoljuk:
 +
:<math>\frac{4!}{3!}=4\,</math>
 +
az összes lehetőségek száma. ''(Ez tekinthető ismétléses permutációnak is.)''
 +
 +
'''5.'''
 +
:<math>\frac{13!}{7!\cdot 6!}\,</math>
 +
mert minden esetet többször, éspedig <math>7!\cdot 6!</math>-szor számoltunk, mert ennyi sorrendje lehet a 7 ill. a 6 egy osztályba tartozó diáknak. ''(Ez tekinthető ismétléses permutációnak is.)''
 +
 +
'''6.''' Ha sorban állnának, 7! lenne az eredmény. Mivel nincs első, ezért a sor bárhol kezdődhet, azt attól még ugyanaz az eset. Ez azt jelenti, hogy minden esetet 7-szer számoltunk, azaz ezzel kell leosztani a 7!-t. Azaz 6!. Vagy kijelölünk egy fixpontot. Innen már csak 6! lehetőség lehet a körön belül a sorba állításra.
 +
 +
'''7. ''' Anna és Gergő kétféleképpen helyezkedhetnek el a körben egymás mellett. Ezután marad 5! a sorrendre, ez <math>2\cdot 5!</math> lehetőség.
 +
 +
'''8.''' A tízesek helyére letesszük a 3-ast. A többi helyre 5!-féleképpen választhatunk számjegyeket, mert minden számnak legalább egyszer szerepelnie kell, amiből az következik, hogy pontosan egyszer.
 +
 +
'''9.''' Ha a háromszög A, B, C csúcsait megkülönböztetnék, akkor az A-nak 5, a B-nek 4, a C-nek 3 csúcsot választhatunk. Ezeknek a lehetőségeknek a száma <math>5\cdot 4\cdot 3</math>. De a sorrend nem számít, azaz ezt 3!-sal el kell osztani: 10. ''(Ez felfogható kombinációnak is: 5 elemből kell kiválasztani 3-at, ez <math>{5}\choose 3</math><math>=10\,</math>.)''
 +
 +
==Ismétléses permutáció==
 +
 +
Legyen ''n'' elemünk és legyen ezek között <math>k_1, k_2, ..., k_l</math> darab azonos (tehát <math>k_1+k_2+...+k_l=n</math>). Ha mindezt az ''n'' elemet felsoroljuk egy ''n'' elemű véges sorozatban, akkor ezeknek az elemeknek egy ismétléses permutációját kapjuk. Ezeknek az elemeknek az összes ismétléses permutációinak számát a következőképpen számíthatjuk ki:
 +
:<math>P_n^{k_1, k_2,\dots, k_l}=\frac{n!}{k_1!\cdot k_2!\cdot\dots\cdot k_l!}</math>

A lap jelenlegi, 2016. szeptember 8., 20:33-kori változata

Lásd még: Matematikai előismeretek

Tartalomjegyzék

Permutáció

Ha adott az {a1, a2, a3, ..., an} véges, n elemű halmaz, akkor ennek egy (ismétlés nélküli) permutációjának nevezzük az elemei egy n elemű véges sorozatba rendezését.

Pl.: ha a halmaz a következő kártyalapokat tartalmazza: {kőr dáma, treff dáma, káró dáma, pikk dáma}, akkor ennek egy permutációja:

(kőr dáma, káró dáma, pikk dáma, treff dáma), vagy (káró dáma, kőr dáma, treff dáma, pikk dáma), stb.

Ezek száma:

P_n=n!\,

Példák

1. Anna, Gabó, Réka és Petra együtt mennek egyetemre. Hányféle sorrendben léphetik át az egyetem küszöbét, ha mind külön lépnek be?

2. Hány különböző ötjegyű szám alkotható a páratlan számjegyekből, ha mindegyik helyiértéken különböző számjegy áll?

3. Hány különböző ötjegyű szám alkotható a páros számjegyekből, ha mindegyik helyiértéken különböző számjegy áll?

4. Kiteszünk az asztalra sorban négy üveget: Fanta, Sprite, Cherry Coke, Traubiszóda. a) Hányféle sorrendben rakhatjuk őket sorba? b) Hányféle sorrendben rakhatjuk őket sorba, ha a Coca Cola termékeket ugyanolyannak vesszük?

5. Hányféleképpen állíthatunk sorba 7 fő 12. A-st és 6 fő 12. B-st, ha a sorrendben csak az számít, hogy melyik osztályban vannak, de az nem, hogy kik ők.

6. Hányféleképpen állíthatunk körbe 7 diákot?

7. Hányféleképpen állhat 7 diák körbe, ha Anna és Gergő feltétlenül egymás mellé kell, hogy kerüljenek?

8. Hány olyan hatjegyű szám létezik, melyben a tízesek helyén a 3-as van, és az 1, 2, 3, 4, 5, 6 számjegyek mindegyike szerepel benne?

9. Egy öt csúcspontú teljes gráf minden csúcsát beszámozzuk. Hány különböző csúcsokból álló háromszöget színezhetünk ki benne?

Megoldások

1. Ez 4 elem összes permutációinak száma: 4!. Vagy először 4 lány közül választhatunk, majd 3, 2, és 1. Ezek egymástól független választások, ezért össze kell szoroznunk őket: 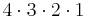4\cdot 3\cdot 2\cdot 1.

2. 5 páratlan számjegy van: 1, 3, 5, 7, 9, ezek összes permutációinak száma a kérdés: ez 5!.

3. 5 páros számjegy van: 0, 2, 4, 6, 8. Ezekből készítünk ötjegyű számokat. Ezek nem kezdődhetnek 0-val, ezért az első számjegy lehet

4. a) Ez 4 elem összes permutációinak száma: 4!. b) Ha a C.C. termékek ugyanolyannak minősülnek (jelöljük őket C-vel, a Traubiszódát T-vel) akkor négy különböző sorozat lehetséges: TCCC, CTCC, CCTC, CCCT. Vagy, ha 4 elemet sorba rendezünk, akkor ezt 4!-féleképpen lehet megtenni. De akkor vannak esetek, amiket többször számoltunk, mert pl. a TFSC és a TFCS esetek ugyanannak minősülnek. Tehát minden esetet az F, C, S minden sorrendje ugyanannak minősül, ez 3!. Ennyiszerese az eredménynek az a) eset megoldása, tehát, ha ezeket az eseteket nem számoljuk:

\frac{4!}{3!}=4\,

az összes lehetőségek száma. (Ez tekinthető ismétléses permutációnak is.)

5.

\frac{13!}{7!\cdot 6!}\,

mert minden esetet többször, éspedig 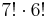7!\cdot 6!-szor számoltunk, mert ennyi sorrendje lehet a 7 ill. a 6 egy osztályba tartozó diáknak. (Ez tekinthető ismétléses permutációnak is.)

6. Ha sorban állnának, 7! lenne az eredmény. Mivel nincs első, ezért a sor bárhol kezdődhet, azt attól még ugyanaz az eset. Ez azt jelenti, hogy minden esetet 7-szer számoltunk, azaz ezzel kell leosztani a 7!-t. Azaz 6!. Vagy kijelölünk egy fixpontot. Innen már csak 6! lehetőség lehet a körön belül a sorba állításra.

7. Anna és Gergő kétféleképpen helyezkedhetnek el a körben egymás mellett. Ezután marad 5! a sorrendre, ez 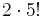2\cdot 5! lehetőség.

8. A tízesek helyére letesszük a 3-ast. A többi helyre 5!-féleképpen választhatunk számjegyeket, mert minden számnak legalább egyszer szerepelnie kell, amiből az következik, hogy pontosan egyszer.

9. Ha a háromszög A, B, C csúcsait megkülönböztetnék, akkor az A-nak 5, a B-nek 4, a C-nek 3 csúcsot választhatunk. Ezeknek a lehetőségeknek a száma 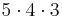5\cdot 4\cdot 3. De a sorrend nem számít, azaz ezt 3!-sal el kell osztani: 10. (Ez felfogható kombinációnak is: 5 elemből kell kiválasztani 3-at, ez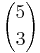 {5}\choose 3=10\,.)

Ismétléses permutáció

Legyen n elemünk és legyen ezek között k1,k2,...,kl darab azonos (tehát k1 + k2 + ... + kl = n). Ha mindezt az n elemet felsoroljuk egy n elemű véges sorozatban, akkor ezeknek az elemeknek egy ismétléses permutációját kapjuk. Ezeknek az elemeknek az összes ismétléses permutációinak számát a következőképpen számíthatjuk ki:

P_n^{k_1, k_2,\dots, k_l}=\frac{n!}{k_1!\cdot k_2!\cdot\dots\cdot k_l!}
A lap eredeti címe: „http://wiki.math.bme.hu/index.php?title=Matematikai_el%C5%91ismeretek_3.&oldid=11927”
Személyes eszközök