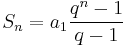Matematikai előismeretek 7.

A MathWikiből
(Változatok közti eltérés)
(→Példák)
(→Példák)
32. sor: 32. sor:
 
:j) <math>\log_4 3\,</math>, <math>\log_4 9\,</math>, <math>\log_4 81\,</math>,
 
:j) <math>\log_4 3\,</math>, <math>\log_4 9\,</math>, <math>\log_4 81\,</math>,
 
:k) <math>\log_5 \frac{1}{9}</math>, <math>\log_5 9</math>, <math>\log_5 \frac{1}{9}\,</math>, <math>\log_5 9\,</math>
 
:k) <math>\log_5 \frac{1}{9}</math>, <math>\log_5 9</math>, <math>\log_5 \frac{1}{9}\,</math>, <math>\log_5 9\,</math>
−
'''2.''' Adjuk meg a ''b'' és ''c'' számok értékét úgy, hogy az <math>a_n=b\cdot c^n</math> sorozat
 
−
:a) szigorúan monoton növekvő, 
 
−
:b) szigorúan monoton csökkenő (fogyó),
 
−
:c) monoton növekvő, 
 
−
:d) monoton csökkenő (fogyó),
 
−
:e) periodikus,
 
−
:f) konstans,
 
−
:g*) csupa pozitív értékű,
 
−
:h*) csupa negatív értékű
 
−
legyen.
 
  
−
'''3.''' Számítsuk ki az n-edik tagot és az első n tag összegét!
+
'''2.''' Számítsuk ki az n-edik tagot és az első n tag összegét!
 
:a) <math>a_1=5</math>, <math>q=-4</math>, <math>n=3</math>
 
:a) <math>a_1=5</math>, <math>q=-4</math>, <math>n=3</math>
 
:b) <math>a_2=6</math>, <math>q=2</math>, <math>n=5</math>
 
:b) <math>a_2=6</math>, <math>q=2</math>, <math>n=5</math>
50. sor: 40. sor:
 
:e) <math>a_1=\log_7 \frac{1}{2}</math>, <math>q=3</math>, <math>n=3</math>
 
:e) <math>a_1=\log_7 \frac{1}{2}</math>, <math>q=3</math>, <math>n=3</math>
 
:f) <math>a_1=\log_2 \sqrt{2}</math>, <math>q=\log_3 \frac{1}{\sqrt[4]{3}}</math>, <math>n=4</math>
 
:f) <math>a_1=\log_2 \sqrt{2}</math>, <math>q=\log_3 \frac{1}{\sqrt[4]{3}}</math>, <math>n=4</math>
 +
 +
'''3.''' Adjuk meg a ''b'' és ''c'' számok értékét úgy, hogy az <math>a_n=b\cdot c^n</math> sorozat
 +
:a) periodikus,
 +
:d) csupa pozitív értékű,
 +
:c) szigorúan monoton növekvő, 
 +
:d) szigorúan monoton csökkenő (fogyó), 
 +
legyen.

A lap 2016. október 13., 20:31-kori változata

Lásd még: Matematikai előismeretek

Mértani sorozat

(a1, a2, a3, a4, ... )

mértani sorozat, ha van olyan q szám, hogy

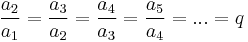\frac{a_2}{a_1}=\frac{a_3}{a_2}=\frac{a_4}{a_3}=\frac{a_5}{a_4}=...=q.

Ilyenkor q-t a mértani sorozat kvociensének nevezzük. Megengedjük, hogy q=0 legyen, ekkor a fenti helyett

a1 tetszőleges, a2 = a3 = ... = 0

Ha (an) mértani sorozat, akkor

a_n=a_1\cdot q^{n-1}\,

nemnegatív tagokra:

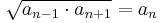\sqrt{a_{n-1}\cdot a_{n+1}}=a_n, minden n-re, ha an − 1 is a sorozat tagja.
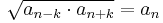\sqrt{a_{n-k}\cdot a_{n+k}}=a_n, minden n-re és k-ra, ha an − k is a sorozat tagja.

Egy nemnegatív sorozat pontosan akkor mértani sorozat, ha bármely egymás követő három tagja közül a második a számtani közepe az elsőnek és a harmadiknak. Általában pedig pontosan akkor mértani, ha 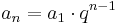a_n=a_1\cdot q^{n-1}\, teljesül rá.

A sorozat első n tagjának összege, azaz Sn = a1 + a2 + a3 + ... + an a következőképpen számítható ki:

S_n=a_1\frac{q^{n}-1}{q-1}

Példák

1. Mértani sorozatot alkotnak-e az alábbi sorozatok? Ha igen, mi a kvóciensük és az első tagjuk? Ha nem, melyik három egymást követő tag hibádzik?

a) 0,5; 1; 1,5
b) 2, 4, 8, 16
c) -2, 4, -8, 16, -32
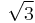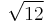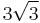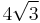
d) \sqrt{3}, \sqrt{12}, 3\sqrt{3}, 4\sqrt{3}
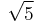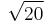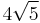
e) \sqrt{5}, \sqrt{20}, 4\sqrt{5}
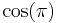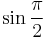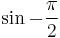f) \cos(\pi)\,, \sin\frac{\pi}{2}, \sin-\frac{\pi}{2}, cos0
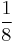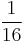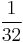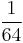
g) \frac{1}{8}, \frac{1}{16}, \frac{1}{32}, \frac{1}{64}
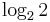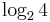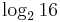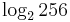h) \log_2 2\,, \log_2 4\,, \log_2 16\,, \log_2 256\,,
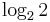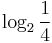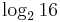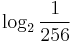i) \log_2 2\,, \log_2 \frac{1}{4}\,, \log_2 16\,, \log_2 \frac{1}{256}\,,
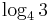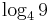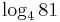j) \log_4 3\,, \log_4 9\,, \log_4 81\,,
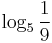k) \log_5 \frac{1}{9}, log59, \log_5 \frac{1}{9}\,, \log_5 9\,

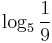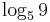
2. Számítsuk ki az n-edik tagot és az első n tag összegét!

a) a1 = 5, q = − 4, n = 3
b) a2 = 6, q = 2, n = 5
c) a3 = 6, q = − 3, n = 4
d) 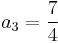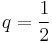a_3=\frac{7}{4}, q=\frac{1}{2}, n = 1
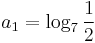e) a_1=\log_7 \frac{1}{2}, q = 3, n = 3
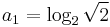f) a_1=\log_2 \sqrt{2}, q=\log_3 \frac{1}{\sqrt[4]{3}}, n = 4

3. Adjuk meg a b és c számok értékét úgy, hogy az 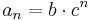a_n=b\cdot c^n sorozat

a) periodikus,
d) csupa pozitív értékű,
c) szigorúan monoton növekvő,
d) szigorúan monoton csökkenő (fogyó),

legyen.

A lap eredeti címe: „http://wiki.math.bme.hu/index.php?title=Matematikai_el%C5%91ismeretek_7.&oldid=12025”
Személyes eszközök