OptMod-2017/Gyakorlat2
(→Szállítási feladat) |
|||
| (egy szerkesztő 12 közbeeső változata nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
= Ismétlés = | = Ismétlés = | ||
| + | |||
| + | == Szállítási feladat == | ||
| + | |||
| + | Adottak raktárak és boltok (telephelyek és felvevõhelyek), adott mennyi áru van a raktárakban (<math>r_1, r_2, \ldots, r_n</math>) és mennyit kell kiszállítani a boltokba(<math>b_1, b_2, \ldots, b_m</math>). Valamint adott, hogy minden raktárból minden más raktárba mennyi a költsége egy egység szállításának (<math>k_{11}, k_{12}, \ldots, k_{1m}, k_{21}, k_{22}, \ldots, k_{nm}</math>). Feladatunk a minimális költséggel kiszolgátlni a boltokat. | ||
| + | |||
| + | [http://www.tankonyvtar.hu/hu/tartalom/tamop412A/2011-0098_operaciokutatas/ch08s03.html Szállítási feladat leírás] | ||
| + | |||
| + | == Hátizsák feladat == | ||
| + | |||
| + | Adott N méretû hátizsákunk, <math>e_1, e_2, \ldots, e_m</math> értékû és <math>s_1, s_2, \ldots, s_m</math> méretû tárgyaink. A feladatunk a lehetõ legértékesebb tárgy kombinációt elpakolni, úgy hogy a hátizsák méretét ne lépjük túl. | ||
= Excel Solver = | = Excel Solver = | ||
| 69. sor: | 79. sor: | ||
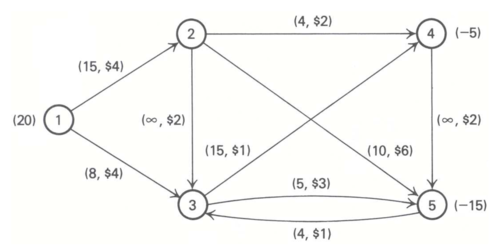
A szállításra használható hálózat vázlata a következő: | A szállításra használható hálózat vázlata a következő: | ||
| − | [[ | + | [[Fájl:Week3_graph.png|500px]] |
Az 1. csúcs a raktárunk, a 4. csúcsba 5 egységet, az 5. csúcsba 15 egységet szállítunk. | Az 1. csúcs a raktárunk, a 4. csúcsba 5 egységet, az 5. csúcsba 15 egységet szállítunk. | ||
Az éleken látható első szám az él kapacitása, míg a második egységnyi áru szállítási költsége. | Az éleken látható első szám az él kapacitása, míg a második egységnyi áru szállítási költsége. | ||
Hogyan szolgáljuk ki a rendeléseket a legolcsóbban? | Hogyan szolgáljuk ki a rendeléseket a legolcsóbban? | ||
| − | |||
== 3. feladat == | == 3. feladat == | ||
| + | |||
| + | Holnap indulunk egy egyhetes túrára a Gellért-hegyre, éppen pakolunk | ||
| + | a 30 literes Mount Everest 2000 túrahátizsákunkba. | ||
| + | A következő tárgyak jönnek számításba: | ||
| + | |||
| + | {| class="wikitable" style="text-align: center; width: 300px;" | ||
| + | |- | ||
| + | | | ||
| + | ! Súly | ||
| + | ! Térfogat | ||
| + | ! Érték | ||
| + | |- | ||
| + | !Jégcsákány | ||
| + | | 4 | ||
| + | | 5 | ||
| + | | 4 | ||
| + | |- | ||
| + | !Keménysisak | ||
| + | | 1 | ||
| + | | 2 | ||
| + | | 7 | ||
| + | |- | ||
| + | !Mászószemüveg | ||
| + | | 0.3 | ||
| + | | 1 | ||
| + | | 5 | ||
| + | |- | ||
| + | !Bőrkabát | ||
| + | | 2 | ||
| + | | 8 | ||
| + | | 4 | ||
| + | |- | ||
| + | !Dupla bélésű kabát | ||
| + | | 4 | ||
| + | | 12 | ||
| + | | 7 | ||
| + | |- | ||
| + | !Kesztyű | ||
| + | | 0.5 | ||
| + | | 1 | ||
| + | | 6 | ||
| + | |- | ||
| + | !Cserezokni | ||
| + | | 0.5 | ||
| + | | 1 | ||
| + | | 2 | ||
| + | |- | ||
| + | !Hálózsák | ||
| + | | 4 | ||
| + | | 11 | ||
| + | | 10 | ||
| + | |- | ||
| + | !Termosz | ||
| + | | 1 | ||
| + | | 3 | ||
| + | | 8 | ||
| + | |- | ||
| + | !Laptop | ||
| + | | 3 | ||
| + | | 5 | ||
| + | | 7 | ||
| + | |- | ||
| + | !Selfie stick | ||
| + | | 1 | ||
| + | | 2 | ||
| + | | 7 | ||
| + | |- | ||
| + | !Kenyér | ||
| + | | 1 | ||
| + | | 2.5 | ||
| + | | 5 | ||
| + | |- | ||
| + | !Szalámi | ||
| + | | 1 | ||
| + | | 1.5 | ||
| + | | 5 | ||
| + | |- | ||
| + | !Svácji bicska | ||
| + | | 0.3 | ||
| + | | 0.1 | ||
| + | | 7 | ||
| + | |- | ||
| + | !Elemlámpa | ||
| + | | 0.3 | ||
| + | | 1 | ||
| + | | 7 | ||
| + | |- | ||
| + | !Elsősegélydoboz | ||
| + | | 1 | ||
| + | | 6 | ||
| + | | 3 | ||
| + | |- | ||
| + | !Kedvenc opkut könyv | ||
| + | | 3 | ||
| + | | 3 | ||
| + | | 6 | ||
| + | |- | ||
| + | !Papírzsebkendő | ||
| + | | 0.2 | ||
| + | | 2 | ||
| + | | 2 | ||
| + | |} | ||
| + | |||
| + | (A súly kilogrammban, a térfogat literben, az érték pedig relatív Fournier-Goldman egységben értendő.) | ||
| + | Ha ügyesek vagyunk, akkor akár 35 litert is bele tudunk préselni a hátizsákba, de így sem szeretnénk | ||
| + | 15 kilónál többet cipelni. | ||
| + | |||
| + | a) Ezen feltételek mellett szeretnénk a boldogságunkat maximalizálni. | ||
| + | |||
| + | b) Ha az optimális megoldás 0,2333 könyvet tartalmaz, akkor elfelejtettük beállítani a változók egészértékűségét. Számoljuk újra! | ||
| + | |||
| + | c) Éppen befejeztük a pakolást, amikor csörög a mobilunk. Anya érdeklődik, hogy ugye a karácsonyra kapott dupla bélésű, 5 méterig vízálló Sherpa (tm) kabátot is visszük. Hosszas alkudozás után sikerül abban megegyezni, hogy legalább 1 kabátot magunkkal viszünk. Hogyan változik a megoldás? | ||
A lap jelenlegi, 2017. szeptember 12., 14:32-kori változata
Tartalomjegyzék |
Ismétlés
Szállítási feladat
Adottak raktárak és boltok (telephelyek és felvevõhelyek), adott mennyi áru van a raktárakban (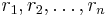 ) és mennyit kell kiszállítani a boltokba(
) és mennyit kell kiszállítani a boltokba(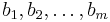 ). Valamint adott, hogy minden raktárból minden más raktárba mennyi a költsége egy egység szállításának (
). Valamint adott, hogy minden raktárból minden más raktárba mennyi a költsége egy egység szállításának (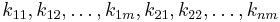 ). Feladatunk a minimális költséggel kiszolgátlni a boltokat.
). Feladatunk a minimális költséggel kiszolgátlni a boltokat.
Hátizsák feladat
Adott N méretû hátizsákunk, 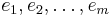 értékû és
értékû és 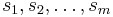 méretû tárgyaink. A feladatunk a lehetõ legértékesebb tárgy kombinációt elpakolni, úgy hogy a hátizsák méretét ne lépjük túl.
méretû tárgyaink. A feladatunk a lehetõ legértékesebb tárgy kombinációt elpakolni, úgy hogy a hátizsák méretét ne lépjük túl.
Excel Solver
1. feladat
Három raktár (S1,S2,S3) szolgálja ki négy diszkont (T1,T2,T3,T4) igényeit. A raktárak kapacitása és a diszkontok megrendelése (megfelelõ mértékegységekben) a következõ:
| S1 | S2 | S3 |
|---|---|---|
| 135 | 56 | 93 |
| T1 | T2 | T3 | T4 |
|---|---|---|---|
| 62 | 83 | 39 | 91 |
Az egységnyi szállítás ára a diszkontokra minden raktárból a következõ:
| T1 | T2 | T3 | T4 | |
|---|---|---|---|---|
| S1 | 132 | 97 | 103 | |
| S2 | 85 | 91 | ||
| S3 | 106 | 89 | 100 | 98 |
Hogyan teljesítsük az összes megrendelést minimális költséggel és a raktárak kapacitásának betartásával?
2. feladat
A raktárunkból két megrendelést szeretnénk kiszolgálni (15, illetve 5 egységet). A szállításra használható hálózat vázlata a következő:
Az 1. csúcs a raktárunk, a 4. csúcsba 5 egységet, az 5. csúcsba 15 egységet szállítunk. Az éleken látható első szám az él kapacitása, míg a második egységnyi áru szállítási költsége. Hogyan szolgáljuk ki a rendeléseket a legolcsóbban?
3. feladat
Holnap indulunk egy egyhetes túrára a Gellért-hegyre, éppen pakolunk a 30 literes Mount Everest 2000 túrahátizsákunkba. A következő tárgyak jönnek számításba:
| Súly | Térfogat | Érték | |
|---|---|---|---|
| Jégcsákány | 4 | 5 | 4 |
| Keménysisak | 1 | 2 | 7 |
| Mászószemüveg | 0.3 | 1 | 5 |
| Bőrkabát | 2 | 8 | 4 |
| Dupla bélésű kabát | 4 | 12 | 7 |
| Kesztyű | 0.5 | 1 | 6 |
| Cserezokni | 0.5 | 1 | 2 |
| Hálózsák | 4 | 11 | 10 |
| Termosz | 1 | 3 | 8 |
| Laptop | 3 | 5 | 7 |
| Selfie stick | 1 | 2 | 7 |
| Kenyér | 1 | 2.5 | 5 |
| Szalámi | 1 | 1.5 | 5 |
| Svácji bicska | 0.3 | 0.1 | 7 |
| Elemlámpa | 0.3 | 1 | 7 |
| Elsősegélydoboz | 1 | 6 | 3 |
| Kedvenc opkut könyv | 3 | 3 | 6 |
| Papírzsebkendő | 0.2 | 2 | 2 |
(A súly kilogrammban, a térfogat literben, az érték pedig relatív Fournier-Goldman egységben értendő.) Ha ügyesek vagyunk, akkor akár 35 litert is bele tudunk préselni a hátizsákba, de így sem szeretnénk 15 kilónál többet cipelni.
a) Ezen feltételek mellett szeretnénk a boldogságunkat maximalizálni.
b) Ha az optimális megoldás 0,2333 könyvet tartalmaz, akkor elfelejtettük beállítani a változók egészértékűségét. Számoljuk újra!
c) Éppen befejeztük a pakolást, amikor csörög a mobilunk. Anya érdeklődik, hogy ugye a karácsonyra kapott dupla bélésű, 5 méterig vízálló Sherpa (tm) kabátot is visszük. Hosszas alkudozás után sikerül abban megegyezni, hogy legalább 1 kabátot magunkkal viszünk. Hogyan változik a megoldás?