OptMod-2017/Gyakorlat4
(→Airplane maintenance) |
(→Elõzõ gyakorlatról maradt) |
||
| (egy szerkesztő 4 közbeeső változata nincs mutatva) | |||
| 60. sor: | 60. sor: | ||
| | | | ||
|} | |} | ||
| − | |||
= Új anyag = | = Új anyag = | ||
| 89. sor: | 88. sor: | ||
!Lisbon | !Lisbon | ||
|38 | |38 | ||
| − | |-9 | + | | -9 |
|12 | |12 | ||
|- | |- | ||
| 118. sor: | 117. sor: | ||
|- | |- | ||
!Sydney | !Sydney | ||
| − | |-33 | + | | -33 |
|151 | |151 | ||
|32 | |32 | ||
| 128. sor: | 127. sor: | ||
|- | |- | ||
!Johannesburg | !Johannesburg | ||
| − | |-26 | + | | -26 |
|28 | |28 | ||
|11 | |11 | ||
| 140. sor: | 139. sor: | ||
The total cost is given by the construction cost plus the expected servicing cost, which depends linearly on the distance an airplane needs to travel to reach the maintenance center (weighted by 50 euro/km). We assume earth is a perfect sphere, so that the shortest (spherical) distance between two points with geographical coordinates (x1, y1) and (x2, y2) is given by the Haversine formula: | The total cost is given by the construction cost plus the expected servicing cost, which depends linearly on the distance an airplane needs to travel to reach the maintenance center (weighted by 50 euro/km). We assume earth is a perfect sphere, so that the shortest (spherical) distance between two points with geographical coordinates (x1, y1) and (x2, y2) is given by the Haversine formula: | ||
| − | <math>d(lat_1, lon_1, lat_2, lon_2) = 2r \ | + | <math>d(lat_1, lon_1, lat_2, lon_2) = 2r \arcsin\sqrt{\sin^2\frac{lat_1-lat_2}{2} + \cos lat_1 * \cos lat_2 * \sin^2\frac{lon_1 - lon_2}{2}}</math> |
where <math>r = 6371\mathrm{km}</math>. | where <math>r = 6371\mathrm{km}</math>. | ||
Formulate a (nonlinear) mathematical program to minimize the operation costs. | Formulate a (nonlinear) mathematical program to minimize the operation costs. | ||
A lap jelenlegi, 2017. szeptember 26., 10:53-kori változata
Tartalomjegyzék |
Elõzõ gyakorlatról maradt
2. feladat
Keressük az f(x) = x − sin(2x) + cos(3x) függvény maximumát a [ − 2,7] intervallumon!
Kövessük grafikonon az optimalizálást! (Options -> All Methods fül -> Show Iteration Results doboz)
Próbáljuk ki az x=0, 1, 2, 3 kezdeti értékekkel, majd próbáljuk ki az x = 0 kezdeti értékkel, multistart opcióval (Options -> GRG Nonlinear fül -> Use Multistart doboz)!
3. feladat
Ábrázoljuk, és minimalizáljuk a Rosenbrock függvényt a ![[-2,2]\times[-1,3]](/upload/math/5/e/0/5e0bba88a366ba6661fabd0eeb3fdd19.png) téglán: f(x,y) = (1 − x)2 + 100(y − x2)2
téglán: f(x,y) = (1 − x)2 + 100(y − x2)2
Indítsuk el a solvert a ( − 2, − 1) pontból, és számoljuk meg, hány lépésben ér célhoz!
Az excelénél szebb ábráért, és egy kis extra információért nézzük meg a Wikipédiát!
Próbáljuk ki a különböző megoldókat itt.
4. feladat
Egy cég két terméket állít elő: C és D.
Ehhez az anyag és a munkaerõszükséglet adott (lásd táblázat).
A cég meg akarja határozni azt az árat ami maximalizálja a profitot.
A C termék elõállítási ára 30$, és a keresletet az 50-0.09*c_ára képlettel közelítik.
A D termék elõállítási ára 20$, és a keresletet az 30-0.14*d_ára képlettel közelítik.
A termékek ésszerű ára 90 és 140 között van.
| Termék | C | D | Készlet |
|---|---|---|---|
| Munka (ora/db) | 2 | 4 | 150 |
| Anyag (kg/db) | 2 | 8 | 220 |
| Költség ($/db) | 30 | 20 | |
| Kereslet (db) | 50-0,09*c_ára | 30-0,14*d_ára |
Új anyag
Airplane maintenance
Boeing needs to build 5 maintenance centers for the Euro-Asian area. The construction cost for each center is 300 million euros in the European area (between 20 W and 40 E) and 150 million euros in the Asian area (between 40 E and 160 E).
Each center can service up to 60 airplanes each year. The centers should service the airports with the highest number of Boeing customers, as detailed in the table below (airport name, geographical coordinates, expected number of airplanes/year needing maintenance).
| Airport | Latitude | Longitude | No. of planes |
|---|---|---|---|
| London | 51 | 0 | 30 |
| Frankfurt | 51 | 8 | 35 |
| Lisbon | 38 | -9 | 12 |
| Zürich | 47 | 8 | 18 |
| Roma | 41 | 12 | 13 |
| Abu Dhabi | 24 | 54 | 8 |
| Moscow | 55 | 37 | 15 |
| Vladivostok | 43 | 132 | 7 |
| Sydney | -33 | 151 | 32 |
| Tokyo | 35 | 139 | 40 |
| Johannesburg | -26 | 28 | 11 |
| New Delhi | 28 | 77 | 20 |
The total cost is given by the construction cost plus the expected servicing cost, which depends linearly on the distance an airplane needs to travel to reach the maintenance center (weighted by 50 euro/km). We assume earth is a perfect sphere, so that the shortest (spherical) distance between two points with geographical coordinates (x1, y1) and (x2, y2) is given by the Haversine formula:
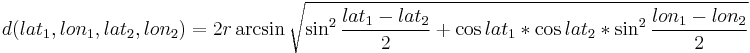
where r = 6371km.
Formulate a (nonlinear) mathematical program to minimize the operation costs.