Perfekt gráfok

Egy G gráfot akkor nevezunk perfektnek, ha χ(G) = ω(G) és ezentul G minden feszitett G' részgráfjára teljesul, hogy χ(G') = ω(G').

Tétel 1

Minden páros gráf perfekt.

Bizonyitás:

Egy G páros gráfnak minden feszitett reszgráfja is páros gráf, ezert eleg belátni, hogy minden páros gráf perfekt. Ez triviálisan igaz, ugyanis egy páros gráf háromszogmentes, es ha legalább egy ele van akkor ω(G) = 2 es χ(G) = 2. Ha nincs ele a gráfnak, akkor pedig ω(G) = χ(G) = 1.

Tétel 2

Minden intervallumgráf perfekt.

Bizonyitás:

Intervallumgráfoknak intervallumgráfok a feszitett reszgráfjai, tehát ismet eleg belátni, hogy minden intervallumgráf perfekt. Azt tudjuk, hogy χ(G) 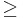$\geq$ ω(G) ezert eleg belátni, hogy ω(G) 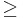$\geq$ χ(G). Legyen ω(G) = n. Szinezzuk a pontoknak megfelelo intervallumokat balrol jobbra, ugy, hogy a szinezetlen intervallumokbol azt szinezzuk eloszor amely leginkább balra van. Ha egy n + 1-edik szint kellene használnunk egy intervallum szinezesehez, az azt jelentene hogy ennek az intervallumnak egy resze benne van n másik intervallumban. Ez azt jelentene hogy van n + 1 meretu klikk, ami ellentmondás.