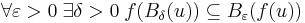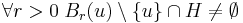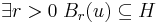Pontbeli határérték, folytonosság
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) (→Folytonosság és határérték) |
Mozo (vitalap | szerkesztései) (→Folytonosság és határérték) |
||
| 1. sor: | 1. sor: | ||
==Folytonosság és határérték== | ==Folytonosság és határérték== | ||
| + | |||
| + | '''Definíció.''' Azt mondjuk, hogy az ''f'': '''R''' <math>\supset\!\to</math> '''R''' függvény '''folytonos''' az ''u'' ∈ Dom(''f'') pontban, ha | ||
| + | :<math>\forall \varepsilon>0\;\exists \delta>0\; f(B_\delta(u))\subseteq B_\varepsilon(f(u))</math> | ||
| + | |||
| + | Ehhez rendkívül hasonló fogalom a határérték, de azt nem Dom(''f'') pontjaiban vizsgáljuk, hanem ehhez közeli pontokban, Dom(''f'') torlódási pontjaiban. Arra van ugyanis szükségünk, hogy matematikailag meg tudjuk fogalmazni a "közeli" fogalmat. | ||
| + | |||
| + | ===Néhány topologikus fogalom=== | ||
| + | Ha ''H'' ⊆ '''R''' valós számhalmaz, akkor az ''u'' ∈ <math>\scriptstyle{\overline{\mathbf{R}}}</math> pontot az ''H'' | ||
| + | *'''torlódási pontjának''' nevezzük, ha | ||
| + | : <math>\forall r>0\;B_r(u)\setminus\{u\}\cap H\ne \emptyset</math> | ||
| + | (ill. ekvivalens módon: B<sub>r</sub>(''u'')\{u} ∩ ''A'' n végtelen) | ||
| + | * '''izolált pontjának''' nevezzük, ha ''u'' ∈ ''H'', de nem torlódási pontja ''H''-nak. | ||
| + | * '''belső pontjának''' nevezzük, ha | ||
| + | :<math>\exists r>0\;B_r(u)\subseteq H</math> | ||
| + | * '''határpontjának''' nevezzük, ha torlódási pontja mind a halmaznak, mind a komplementerének. | ||
'''Definíció.''' Azt mondjuk, hogy az ''f'': '''R''' <math>\supset\!\to</math> '''R''' függvény '''folytonos''' az ''u'' ∈ Dom(''f'') pontban, ha | '''Definíció.''' Azt mondjuk, hogy az ''f'': '''R''' <math>\supset\!\to</math> '''R''' függvény '''folytonos''' az ''u'' ∈ Dom(''f'') pontban, ha | ||
:<math>\forall \varepsilon>0\;\exists \delta>0\; f(B_\delta(u))\subseteq B_\varepsilon(f(u))</math> | :<math>\forall \varepsilon>0\;\exists \delta>0\; f(B_\delta(u))\subseteq B_\varepsilon(f(u))</math> | ||
A lap 2020. október 27., 22:43-kori változata
Folytonosság és határérték
Definíció. Azt mondjuk, hogy az f: R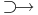 
R függvény folytonos az u ∈ Dom(f) pontban, ha
Ehhez rendkívül hasonló fogalom a határérték, de azt nem Dom(f) pontjaiban vizsgáljuk, hanem ehhez közeli pontokban, Dom(f) torlódási pontjaiban. Arra van ugyanis szükségünk, hogy matematikailag meg tudjuk fogalmazni a "közeli" fogalmat.
Néhány topologikus fogalom
Ha H ⊆ R valós számhalmaz, akkor az u ∈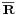 
pontot az H
- torlódási pontjának nevezzük, ha
(ill. ekvivalens módon: Br(u)\{u} ∩ A n végtelen)
- izolált pontjának nevezzük, ha u ∈ H, de nem torlódási pontja H-nak.
- belső pontjának nevezzük, ha
- határpontjának nevezzük, ha torlódási pontja mind a halmaznak, mind a komplementerének.
Definíció. Azt mondjuk, hogy az f: R 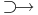R függvény folytonos az u ∈ Dom(f) pontban, ha
