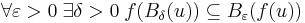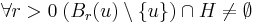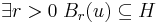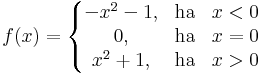Pontbeli határérték, folytonosság
A MathWikiből
A lap korábbi változatát látod, amilyen Mozo (vitalap | szerkesztései) 2020. október 27., 23:02-kor történt szerkesztése után volt.
Tartalomjegyzék |
Folytonosság és határérték
Definíció. Azt mondjuk, hogy az f: R 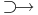 R függvény folytonos az u ∈ Dom(f) pontban, ha
R függvény folytonos az u ∈ Dom(f) pontban, ha
Ehhez rendkívül hasonló fogalom a határérték, de azt nem Dom(f) pontjaiban vizsgáljuk, hanem ehhez közeli pontokban, Dom(f) torlódási pontjaiban. Arra van ugyanis szükségünk, hogy matematikailag meg tudjuk fogalmazni a "közeli" fogalmat.
Néhány topologikus fogalom
Ha H ⊆ R valós számhalmaz, akkor az u ∈ 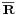 pontot az H
pontot az H
- torlódási pontjának nevezzük, ha
(ill. ekvivalens módon: (Br(u)\{u}) ∩ H végtelen) jelben: 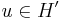 .
.
- izolált pontjának nevezzük, ha u ∈ H, de nem torlódási pontja H-nak.
- belső pontjának nevezzük, ha
jelben: 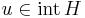 .
.
- határpontjának nevezzük, ha torlódási pontja mind a halmaznak, mind a komplementerének.
A folytonosság definíciójából következik, hogy 1. a polinomok folytonosak, 2. izolált pontban a függvények folytonosak.
Példa
1. a) Mik az izolált, torlódási, belső pontjai?
1. b) Folytonos-e az inverze?
Határérték
Definíció. Legyen f: R 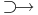 R függvény, u ∈ Dom(f)' és A ∈ u ∈
R függvény, u ∈ Dom(f)' és A ∈ u ∈ 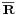 . Ekkor
. Ekkor