Programozás 2/2007
Tartalomjegyzék |
Segédanyag
A C nyelvhez
Juhász István-Kósa Márk-Pánovics János: C példatár, 2005, PANEM.
A feladatok megoldásai megtalálhatóak a http://infotech.inf.unideb.hu/konyvek/cpeldatar/ oldalon. Minden kód HTML-ben van, ezért vagy szövegfájlként kell menteni (save as), vagy ki kell másolni egy fájlba (copy-paste). Az összes forráskód tömörítve letölthető innen.
Az Informatika 2 tárgy wiki oldala.
A Ruby nyelvhez
Az Informatika 2 tárgy wiki oldala, és az ott található linkek.
Gyakorló feladatok
C Feladatok
Az alábbi feladatok részben a példatár példáinak kis módosításai vagy pontosításai, részben a tavalyiak ismétlései, de szerepel egy-két egyéb feladat is (néhol a feladat után kerek zárójelben az ismétlendő anyag szerepel). A SIO használatának felevenítésére egy-egy feladatot ott is kitűzünk.
- (2.3) Írjunk programot, mely egy beolvasott évszámról eldönti, hogy szökőév-e. Ha a beolvasott szám nem pozitív, írja ki, hogy nem évszám. (if, else if, else, printf, scanf, logikai műveletek: &&, ||..., %)
- (2.11 a) Írjunk programot, mely összeadja az egészeket 1-től n-ig az n(n + 1) / 2 képletet használata nélkül. (for, i++, +=)
- (2.17 b) Írjunk nem rekurzív programot egyetlen while-ciklussal két pozitív egész szám legnagyobb közös osztójának meghatározására, azaz az Euklideszi algoritmusra. (while)
- (2.20) Olvassunk be egy karakterláncot, és számoljuk meg a kisbetűk számát az első olyan karakterig, amely nem az angol ábécé egy betűje, majd írjuk ki ezt a számot. (do while, char, getchar, islower, isalpha)
- (3.3) Írjunk olyan programot, mely egy tömbbe beolvas 10 egész számot, majd eldönti, hogy van-e köztük két olyan, amelyek szorzata 48. (egymásba ágyazott for ciklusok)
- (3.7) Írjunk olyan függvényt, mely egy adott
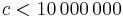 pozitív egészhez meghatározza azt a legnagyobb egész n számot, melyre léteznek olyan x és y pozitív egész számok, hogy xFn − 1 + yFn = c, ahol Fn az n-edik Fibonacci-szám (F0 = 0, F1 = 1).
pozitív egészhez meghatározza azt a legnagyobb egész n számot, melyre léteznek olyan x és y pozitív egész számok, hogy xFn − 1 + yFn = c, ahol Fn az n-edik Fibonacci-szám (F0 = 0, F1 = 1).
- ismétlés: tavalyi honlapról bombaz.c
- (3.7 Nyolc királynő probléma - jeles szint) Írjunk programot, mely egy
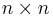 -es sakktáblán megkeresi n királynő összes olyan elhelyezéseit, ahol egyik királynő sem üti semelyik másikat, és azokat kiírja a képernyőre!
-es sakktáblán megkeresi n királynő összes olyan elhelyezéseit, ahol egyik királynő sem üti semelyik másikat, és azokat kiírja a képernyőre!
- (13.2) Szerelvényrendezés
- (9.1) NyargaLó feladat
- (SET! játék) A SET! egy 81 kártyából álló játék. Minden kártyán lévő jelet 4 tulajdonság jellemez, ezek mindegyikéből 3-3 változat fordul elő (így a kártyák maximális száma 34 = 81 lehet). A 4 tulajdonság:
(a) a kártyán lévő figurák száma (1, 2 vagy 3);
(b) a kártya figuráinak színe (piros, zöld, lila);
(c) a figurák telítettsége (üres, félig kitöltött, kitöltött);
(d) a figurák alakja (Rombusz, Téglalap, Hullám).
Pl. az egyik kártyán van 3 piros félig kitöltött rombusz (3PFR). Azt mondjuk, hogy 3 kártya ,,set"-et alkot, ha a 3 kártya minden tulajdonság szerint vagy azonos, vagy különböző. Pl. setet alkot az 1PKR, 2PKT, 3PKH, mert szám szerint mind különböző (123), szín szerint mind azonos (P), kitöltöttség szerint mind azonos (K), alak szerint mind különböző (RTH). Írjunk programot, mely beolvas 3 és 81 közé eső számú kártyaleírást, és kiírja az ezekből kiválasztható összes setet. A helyes kártyaleírás 4 karakterből áll, az első az 1,2 vagy 3 valamelyike, a második a P, Z, L, a harmadik az U, F, K, a negyedik az R, T, H karakterek valamelyike. Pl. egy lehetséges input:
3LKT
1PUR
3PKR
2PFR
3ZKH
amire a helyes válasz:
1PUR 2PFR 3PKR
3PKR 3ZKH 3LKT
A játék leírása megtalálható a wikipédián is, de van online változata, több is, sőt beviszek egy valódi példányt, úgyhogy ,,élőben" is ki lehet próbálni.
Ruby feladatok
- (fill – sokszög kitöltése)
Egy fekete-fehér kép egy rácsnégyzetekből álló téglalap, melyben minden kis négyzetnek saját színe van: fekete (1) vagy fehér (0). A téglalap szélessége és magassága is egy pozitív egész szám. A bal alsó sarok a (0,0). A kis négyzeteket más néven képpontnak vagy pixelnek nevezzük. Az üres kép csupa fehér képpontból áll.
Egy fekete-fehér képet az alábbi módon kell PBM-fájlba írni:
1. a "P1 " string
2. a kép szélessége 10-es számrendszerben (pl. "30")
3. szóköz (" ")
4. a kép magassága 10-es számrendszerben (pl. "20")
5. soremelés (a "\n" string)
6. Minden sorra (felülről lefele):
7. A soron belül minden képpontra (balról jobbra): "0", ha a képpont fehér, és "1", ha fekete
8. soremelés (a "\n" string)
Megjegyzés: Ha egy, a fenti tartalmú fájlnak .pbm kiterjesztést adunk, akkor a benne levő képet (Linux alatt) sok képnézegető programmal meg tudjuk nézni (Windows alatt is vannak ilyenek), például a GQview programmal így: gqview fájlnév.pbm
Megjegyzés: A PBM fájlformátum a fentinél kicsit bővebb szintaxist is megenged, ezek a bővítmények a feladat megoldásához nem szükségesek.
Egy útvonal (angolul path) képpontok listája. Az útvonal azt a sokszöget jelöli ki a síkon, melynek csúcsai a listában szereplő képpontok a listabeli sorrendben. Élnek tekintjük a lista két szomszédos eleme közti szakaszt, továbbá az első és utolsó csúcspontja közötti szakaszt. A lista legalább három csúcspontból áll. Csak konvex sokszögek megengedettek, és az élek meredeksége 45 foknak többszöröse kell legyen.
Egy útvonalat konvexnek nevezünk, ha bármely két szomszédos élére igaz, hogy az általuk bezárt előjeles szög 0-nál nagyobb és 180 foknál kisebb; vagy bármely két szomszédos élére igaz, hogy az általuk bezárt előjeles szög 0-nál kisebb és -180 foknál nagyobb. Szomszédosnak tekintünk két élt, ha van közös csúcspontjuk. (A konvexség fenti definíciójának intuitív magyarázata: egy útvonal konvex, ha körbemenve rajta mindig balra vagy mindig jobbra kell fordulni.)
Egy útvonal kitöltött képének azt a fekete konvex sokszöget nevezzük (belső pontokkal együtt), melyet az útvonal határol. Pontosabban, egy útvonal kitöltött képének kirajzolásakor az alábbi képpontokat kell befeketíteni:
1. az útvonal csúcspontjai;
2. az útvonal élei, mint szakaszok képpontjai (hogy pontosan mely képpontok érintettek, az egyértelmű, mivel a szakaszmeredekség 45 fok többszöröse);
3. az összes olyan képpontot, amely az előző pontban felrajzolt szakaszok által definiált konvex sokszög belsejében található.
A feladat:
Írjon egy programott Ruby nyelven, amely a bemenetről beolvasott csúcspontok által definiált sokszöget kitöltve kirajzolja, és az eredményt PBM formátumban kiírja a fenti módon. (Könnyítés: első lépésként olyan program írása, mely a sokszöget kirajzolja, de nem tölti ki, és esetleg a konkávot is megengedi.)
A program bemenetének első sorában két egész szám található szóközzel elválasztva. Az első a kép szélessége (w), a másik a kép magassága (h). A kép kezdetben teljesen fehér.
A bemenet további sorai (legalább 3 db) egy konvex útvonal csúcspontjait tartalmazzák sorrendben. Minden sor egy x koordinátát, egy szóközt és egy y koordinátát tartalmaz. A sorokat egy "-1 -1\n" sor zárja. Teljesül, hogy 0 ≤ x < w és 0 ≤ y < h.
Ha a bemeneten megadott útvonal élei között van olyan, melynek meredeksége nem 45 fok többszöröse, akkor a program "ANGLE\n"-t ír ki. Ellenkező esetben, ha a bemenetben megadott útvonal nem konvex sokszöget határoz meg, akkor a program "NOT_CONVEX\n"-et ír ki. Ellenkező esetben a program a megadott szélességű és magasságú fehér képre feketével felrajzolja a bemeneten megadott útvonal kitöltött képét, és a kapott képet a fenti módon PBM formátumban kiírja.
A program ezután új képpel folytatja a bemenet beolvasását mindaddig, amíg nincs vége.
Mintabemenet
4 4
0 0
3 0
0 3
-1 -1
4 3
0 0
3 0
0 2
-1 -1
11 5
1 4
9 4
9 1
1 1
-1 -1
Mintakimenet
P1 4 4
1000
1100
1110
1111
ANGLE
P1 11 5
01111111110
01111111110
01111111110
01111111110
00000000000
- (drawone – rajzolóprogram – a Draw45 rajzolási modell)
A Draw45 rajzolási modell pixeles képek előállítására használható. A modellben a rajzolóprogram a bemenetéről beolvassa, majd végrehajtja a rajzoló utasításokat, és végül kiírja a kimenetére az eredményül kapott képet.
A pixeles kép egy rácsnégyzetekből álló téglalap, melyben minden kis négyzetnek saját színe van. A téglalap szélessége és magassága is egy pozitív egész szám. A bal alsó sarok a (0,0). A kis négyzeteket más néven képpontnak vagy pixelnek nevezzük.
Egy szín három komponensből áll: piros, kék és zöld. Minden komponens egy [0,255]-beli egész szám. A színt az egyes komponensek összeadó színkeverés szerinti egyesítésével kell megjeleníteni, például a (255,127,0) szín valahol a piros és a narancssárga között van, mert sok piros és kevés zöld keveréke. (További részletek a színek ily módon történő összeállításáról az RGB Wikipedia-lapon.)
Egy képet az alábbi módon kell fájlba írni:
- a "P6 " string
- a kép szélessége 10-es számrendszerben (pl. "30")
- szóköz (" ")
- a kép magassága 10-es számrendszerben (pl. "20")
- a " 255\n" string
- Minden képpontra (felülről lefele, azon belül balról jobbra):
- egy bájt, ami a képpont színének piros komponense (pl. Ruby-ban 255.chr)
- egy bájt, ami a képpont színének kék komponense (pl. Ruby-ban 127.chr)
- egy bájt, ami a képpont színének zöld komponense (pl. Ruby-ban 0.chr)
Megjegyzés: Ha egy, a fenti tartalmú fájlnak .ppm kiterjesztést adunk, akkor a benne levő képet a legtöbb képnézegető programmal meg tudjuk nézni, például a GQview programmal így: gqview fájlnév.ppm
Egy útvonal (angolul path) képpontok listája. Az útvonal azt a sokszöget jelöli ki a síkon, melynek csúcsai a listában szereplő képpontok a listabeli sorrendben. Csak konvex sokszögek megengedettek, és az élek meredeksége 45 foknak többszöröse kell legyen.
Egy útvonalat konvexnek nevezünk, ha bármely két szomszédos élére igaz, hogy az általuk bezárt előjeles szög 0-nál nagyobb és 180 foknál kisebb; vagy bármely két szomszédos élére igaz, hogy az általuk bezárt előjeles szög 0-nál kisebb és -180 foknál nagyobb. Élnek tekintjük a lista első és utolsó csúcspontja közötti élt is. Szomszédosnak tekintünk két élt, ha van közös csúcspontjuk. (A konvexség fenti definíciójának intuitív magyarázata: egy útvonal konvex, ha körbemenve rajta mindig balra vagy mindig jobbra kell fordulni.)
Egy alakzat (angolul shape) az alábbi tulajdonságok összessége: útvonal, szín, kitöltöttség. A kitöltöttség lehet üres vagy teli.
Az alakzatot az alábbi módon kell egy képre felrajzolni:
- Az alakzat útvonalának csúcspontjait az alakzat színére kell festeni.
- Az alakzat útvonalában szereplő összes szomszédos csúcspont-pár által definiált szakasz minden képpontját az alakzat színére kell festeni. Hogy pontosan mely képpontok érintettek, az egyértelmű, mivel a szakaszmeredekség 45 fok többszöröse.
- Ha az alakzat kitöltöttsége teli, akkor az összes olyan képpontot az alakzat színére kell festeni, amely az előző pontban felrajzolt szakaszok által definiált konvex sokszög belsejében található.
- A rajzolóprogram egy fehér kezdőképből indulva beolvassa és végrehajta a bemenetén található utasításokat, majd kiírja az eredményül kapott képet a fent definiált formátumban. Ha a bemenet hibás (pl. értelmetlen utasítás szerepel rajta, vagy nem konvex útvonalat kéne definiálni), akkor az első hibánál a program hibaüzenetet ír ki a kimenetére, majd befejezi futását (tehát az eredmény-képet nem írja ki).
Az utasítások az alábbiak:
- #akármi, ahol akármi tetszőleges nemüres string (a sor végéig tart). Ez az utasítás csak egy megjegyzés a bemeneten, nem csinál semmit.
- CANVAS w h, ahol w és h pozitív egész számok. Az aktuális képet új, fehér (csupa (255,255,255) színű) képre cseréli, melynek szélessége w, magassága h.
- PATH p x1 y1 x2 y2 x3 y3 ..., ahol p az angol ábécé kisbetűiből álló, nemüres string, x1 stb. egész szám és ... további páros sok egész szám, szóközzel elválasztva. Egy p nevű útvonalat definiál, melynek csúcspontjai (x1,y1), (x2,y2), (x3,y3) stb. Csak konvex sokszög megengedett.
- RGB c r g b, ahol c az angol ábécé kisbetűiből álló, nemüres string; r, g és b pedig [0,255]-beli egész számok. Egy c nevű színt definiál, amely a megadott összetevőkből áll.
- SHAPE s p c f, ahol s, p és c az angol ábécé kisbetűiből álló, nemüres string; f pedig vagy 0, vagy 1. Egy s nevű alakzatot definiál, amelynek útvonala p, színe c és kitöltöttsége f (0 jelöli az üreset, 1 a telit).
- DRAW s x y, ahol s az angol ábécé kisbetűiből álló, nemüres string; x és y egész számok. Az aktuális képre kirajzolja az s nevű alakzatot (x,y)-nal eltolva (vagyis minden csúcspont koordinátáihoz x-et ileltve y-t hozzáadva).
Egy egész szám vagy 0, vagy egy nem nullával kezdődő, tízes számrendszerbeli egész szám, vagy egy - jel, majd egy nem nullával kezdődő, tízes számrendszerbeli egész szám.
A program működésének lépései a következők:
- Az aktuális kép előkészítése CANVAS 200 100 végrehajtásával.
- Az alábbiak ismétlése, amíg van mit beolvasni a bemenetről:
- A bemenetről egy sort be kell olvasni, és azt utasításnak kell értelmezni.
- Ha a beolvasás során hiba keletkezik (pl. ismeretlen utasításnév, hiányzó paraméter, túl sok paraméter, PATH esetén páratlan sok vagy 6-nál kevesebb koordináta, hibás formátumú paraméter, fölösleges 0 az egész szám elején, ékezetes betű egy névben, CANVAS esetén 1-nél kisebb szám), akkor SYNTAX hibát kell jelezni.
- Ha a PATH p, az RGB c vagy a SHAPE s neve már definiálva van, akkor DEFINED hibát kell jelezni. Egy név definiáltnak számít, ha egy korábbi tetszőleges PATH, RGB vagy SHAPE parancs első paramétere volt.
- Ha a SHAPE p vagy c neve, vagy a DRAW s neve még nincs definiálva, akkor UNDEFINED hibát kell jelezni.
- Ha a PATH-nak van olyan éle, amelynek vízszintessel bezárt szöge nem 45 fok többszöröse, akkor ANGLE hibát kell jelezni.
- Ha a PATH csúcspontjai nem konvex sokszöget definiálnak, akkor NOT_CONVEX hibát kell jelezni.
- Ha a SHAPE eltolt alakzata kilóg a képből, akkor BOUNDS hibát kell jelezni.
- Az utasítást a fent definiált módon végre kell hajtani.
- Az aktuális képet a fent definiált formátumban ki kell írni a kimenetre.
A hibajelzés az alábbi módon történik. A program számolja, hány sort olvasott már be. Ha a futás során e hibát kell jelezni, amely az n-edik sor beolvasása után derült ki, akkor a program az e IN n hibaüzenetet írja ki egy soremeléssel lezárva, majd kilép (Ruby-ban Process.exit()). Példa hibaüzenet: NOT_CONVEX IN 42
Első részfeladat: Írjon programot Ruby nyelven, amely a Draw45 rajzolási modellt valósítja meg, azzal az egyszerűsítéssel, hogy az utasításokat csak a SYNTAX ellenőrzésig bezárólag hatja végre. Tehát a program kimenete vagy egy 200x100-as fehér kép, vagy egy SYNTAX hibaüzenet.
Második részfeladat: Írjon programot Ruby nyelven, amely a Draw45 rajzolási modellt valósítja meg azzal az egyszerűsítéssel, hogy a teli kitöltöttségű alakzatokat nem rajzolja ki, tehát a SHAPE utasítás nem rajzol semmit, ha az f paramétere 1.
Harmadik részfeladat: Írjon programot Ruby nyelven, amely A Draw45 rajzolási modellt teljes mértékben megvalósítja.
Mintabemenet (a mintakimenet egy svájci zászló: piros alapon fehér kereszt)
RGB piros 218 22 3 RGB feher 254 255 252 CANVAS 125 125 PATH pirosnegyzet 0 0 124 0 124 124 0 124 PATH fekvoteglalap 21 50 103 50 103 74 21 74 PATH alloteglalap 50 21 74 21 74 103 50 103 SHAPE pirosnegyzets pirosnegyzet piros 1 SHAPE fekvoteglalaps fekvoteglalap feher 1 SHAPE fekvoteglalaps fekvoteglalap feher 1 DRAW pirosnegyzets 0 0 DRAW fekvoteglalaps 0 0 DRAW fekvoteglalaps 0 0