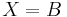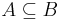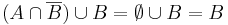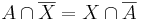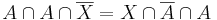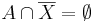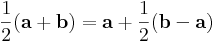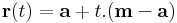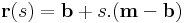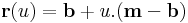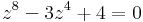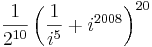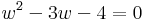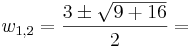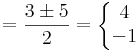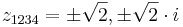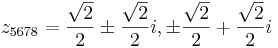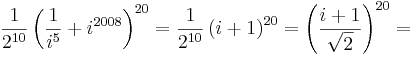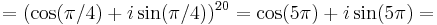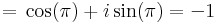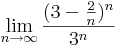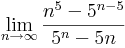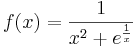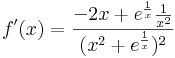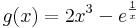Szerkesztő:Mozo/A1 feladatok 1.
Tartalomjegyzék |
Halmazok
- Egyszerűsítse az alábbi kifejezéseket!
-
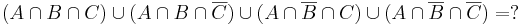
-
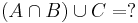 , ha
, ha 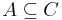 .
.
-
- Oldja meg az alábbi halmazegyenleteket, X-re!
-
- Igazolja minden A, B, C halmazra, hogy
-
- Igazolja minden
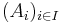 és
és 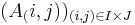 halmazrendszerre, hogy
halmazrendszerre, hogy
-
Megoldás.
1.1. Legyen D a feladatban szereplő halmaz és legyen U = A U B U C a komplementerképzés alaphalmaza! Emeljünk ki A-t!
A második tényező első két tagjából kiemelhetünk B-t a második két tagjából B komplementert:
ekkor a halmaz és komplementere kiadja U-t, így:
Tehát D = A.
Vagy Boole-algebrai formalizmusban:
1.2.
az elnyelési tulajdonság miatt és mert A ⊆ C pontosan azt jelenti, hogy A U C = C.
2.1. Legyen a komplementerképzés univerzuma U. Tegyük fel, hogy van megoldás. Eltünik az X komplementer a bal oldalról, ha mindkét oldalt elmetszük X-szel:
ez utóbbi pontosan azt jelenti, hogy X ⊆ B. Emellett a feltétel mellett B-vel a baloldalon "beuniózva":
amiből következik, hogy B ⊆ X és A ⊆ X. Ez azt jelenti, hogy ha van megoldás, akkor az egyértelmű éspedig
Most vizsgáljuk meg a megoldhatóság feltételét. Azt kaptuk, hogy ha van megoldás, akkor A ⊆ X = B, vagyis
De ez elégséges feltétele is a megoldhatóságnak, ugyanis ekkor az X = B helyettesítés kielégíti az egyenletet:
2.2.
vagyis
Ha van megoldás és bemetszünk mindkét oldalon A-val, akkor
azaz A ⊆ X, de az egyenlet szimmetrikus az A és az X felcserélésére, ezért X ⊆ A is teljesül, amiből X = A, ha van megoldás. Márpedig az egyenletet az X = A kielégíti.
3.
Geometria vektorokkal
1. Igazoljuk, hogy a paralelogramma átlói felezik egymást!
Mo. Legyen egy csúcsból kiinduló két oldalvektor a és b. Az átlók pontjai:
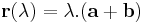 ,
, ![\lambda\in[0,1]](/upload/math/a/d/a/ada29722c713d4d8a571d9a4ce353ae6.png)
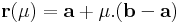 ,
, ![\mu\in[0,1]](/upload/math/4/0/c/40c22bb74ef18fef1869b28e9a8a702b.png)
Világos, hogy az átlók felezéspontjai a λ=μ=1/2 értékeknél vannak. Ezek a pontok pedig egybeesnek, hisz
2. Igazoljuk, hogy ha a kezdőpontot a háromszög körül írható körének középpontjában veszük föl, akkor onnan felírva a csúcsokba mutató a, b és c vektorok m = a + b + c összege a magasságpont.
Mo. m - a merőleges a szemben fekvő oldallal, hisz:
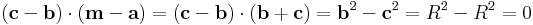
m - a tehát irányvektora egy magasságvonalnak, ugyanígy m - b és m - c is. Emiatt a magasságegyenesek:
De ezek egy pontban találkoznak, az m-ben.
Sík és egyenes
Van-e olyan sík, mely tartalmazza az
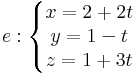 illetve
illetve 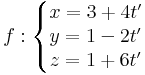
egyeneseket?
Komplex számok
- Oldja meg az alábbi egyenletet a komplex számok halmazán!
- Adja meg a következő kifejezés értékét algebrai alakban!
Megoldás.
1. w = z4 új ismeretlennel:
ami a megoldóképlet szerint:
ahol a négyzetgyököt a komplex kétértékű értelemben kell venni.
Ezeknek könnyű előállítani a negyedik gyökeiket. Az abszolút értékek:
![\sqrt[4]{4}=\sqrt{2}](/upload/math/f/2/3/f23db380b0199b416eb98cac80e799d2.png) és
és 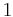 ,
,
így
2.
Sorozatok
- Igazak-e a következő kijelentések?
- Ha egy sorozat monoton és korlátos, akkor konvergens.
- Ha egy sorozat monoton és van konvergens részsorozata, akkor konvergens.
- Ha egy sorozat divergens, akkor az (1/n)-nel vett szorzata konvergens.
- Ha egy sorozat felülről nem korlátos, akkor nincs konvergens részsorozata.
- Ha egy sorozat a + végtelenbe tart, akkor van a + végtelenhez tartó részsorozata.
- Ha egy konvergens sorozat minden tagja pozitív, akkor a határértéke is pozitív.
- Ha (an+1
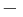 an) nullsorozat, akkor (an) konvergens.
an) nullsorozat, akkor (an) konvergens.
- Mennyi?
-
- Konvergens-e?
-
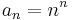 esetén
esetén 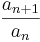
-
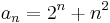 esetén
esetén 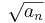
-
Függvényvizsgálat
Vizsgáljuk meg monotonitás és szélsőérték szempontjából.
b)
zh: hány megoldása van az
egyenletnek? x pozitív,
deriváltja pozitív, tehát szig. mon nő, azaz legfeljebb csak egy megoldás van. Bolzano-tételből köv., hogy van megoldás. Legyen ez xM. Előjele: előtte +, utána -. Negatívokra +.
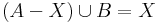
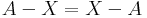

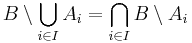
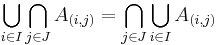
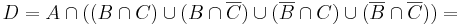
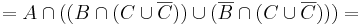
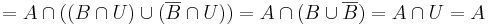
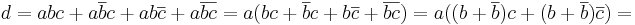
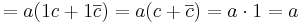
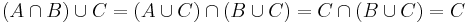
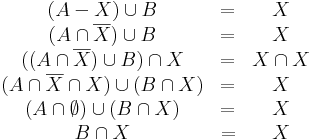
![[\;X =\; ]\quad\quad(A\cap \overline{X}) \cup B =(A\cup B)\cap (\overline{X}\cup B)\supseteq (A\cup B)\cap (\overline{X}\cup X)=(A\cup B)\cap U =A\cup B](/upload/math/2/2/a/22a2065200b5777f3f31a4cfd4bda2b6.png)