Szerkesztő:Mozo/A1 feladatok 1.
Halmazok.
- Egyszerűsítse az alábbi kifejezéseket!
- Oldja meg az alábbi halmazegyenleteket, X-re!
-
Megoldás. 1. Legyen D a feladatban szereplő halmaz és legyen U = A U B U C a komplementerképzés alaphalmaza! Emeljünk ki A-t!
A második tényező első két tagjából kiemelhetünk B-t a második két tagjából B komplementert:
ekkor a halmaz és komplementere kiadja U-t, így:
Tehát D = A.
Boole-algebrai formalizmusban:
2.1. Legyen a komplementerképzés univerzuma U. Tegyük fel, hogy van megoldás. Eltünik az X komplementer a bal oldalról, ha mindkét oldalt elmetszük X-szel:
ez utóbbi pontosan azt jelenti, hogy X ⊆ B. Emellett a feltétel mellett B-vel a baloldalon "beuniózva":
amiből következik, hogy B ⊆ X és A ⊆ X. Ez egyfelől azt jelenti, hogy ha van megoldás, akkor az egyértelmű éspedig
Most vizsgáljuk meg a megoldhatóság feltételét. Azt kaptuk, hogy ha van megoldás, akkor A ⊆ X = B, vagyis A ⊆ B. De ez elégséges feltétele is a megoldhatóságnak, ugyanis ekkor A U B = B és az egyenlet:
az elnyelési tulajdonság miatt.

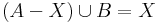
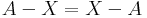
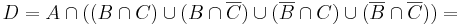
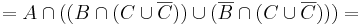
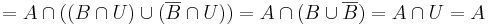
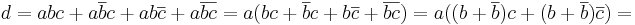
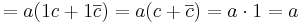
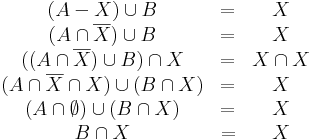
![[\;X =\; ]\quad\quad(A\cap \overline{X}) \cup B =(A\cup B)\cap (\overline{X}\cup B)\supseteq (A\cup B)\cap (\overline{X}\cup X)=(A\cup B)\cap U =A\cup B](/upload/math/2/2/a/22a2065200b5777f3f31a4cfd4bda2b6.png)
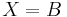
![[\;X =\; ]\quad\quad(A\cap \overline{X}) \cup B =(A\cup B)\cap (\overline{X}\cup B)= B\cap (\overline{X}\cup B)=B](/upload/math/f/e/a/fea336e40b8af78e0d0b7615ffd068c8.png)