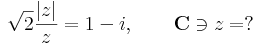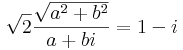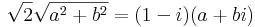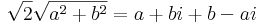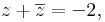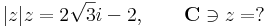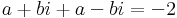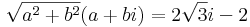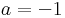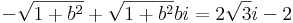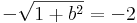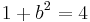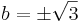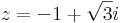Szerkesztő:Mozo/A1 feladatok 2.

A MathWikiből
(Változatok közti eltérés)
(→Algebrai alak)
(→Algebrai alak)
6. sor: 6. sor:
 
:<math>\sqrt{2}\frac{|z|}{z}=1-i,\quad\quad\mathbf{C}\ni z=?</math>
 
:<math>\sqrt{2}\frac{|z|}{z}=1-i,\quad\quad\mathbf{C}\ni z=?</math>
  
−
''Mo.'' Írjuk fel az ismeretlent algebrai alakban: ''z'' = ''a'' + ''b'' i
+
''Mo.'' Világos, hogy a ''z'' = 0-t kizárhatjuk.
 +
 
 +
Írjuk fel az ismeretlent algebrai alakban: ''z'' = ''a'' + ''b'' i
  
 
:<math>\sqrt{2}\frac{\sqrt{a^2+b^2}}{a+bi}=1-i</math>
 
:<math>\sqrt{2}\frac{\sqrt{a^2+b^2}}{a+bi}=1-i</math>
22. sor: 24. sor:
 
:<math>z+\overline{z}=-2,</math>
 
:<math>z+\overline{z}=-2,</math>
 
:<math>|z|z=2\sqrt{3}i-2,\quad\quad\mathbf{C}\ni z=?</math>
 
:<math>|z|z=2\sqrt{3}i-2,\quad\quad\mathbf{C}\ni z=?</math>
 +
 +
''Mo.'' Írjuk fel az ismeretlent algebrai alakban: ''z'' = ''a'' + ''b'' i
 +
:<math>a+bi+a-bi=-2\,</math>
 +
:<math>\sqrt{a^2+b^2}(a+bi)=2\sqrt{3}i-2\,</math>
 +
 +
:<math>a=-1\,</math>
 +
:<math>-\sqrt{1+b^2}+\sqrt{1+b^2}bi=2\sqrt{3}i-2\,</math>
 +
:<math>-\sqrt{1+b^2}=-2\,</math>
 +
 +
:<math>1+b^2=4\,</math>
 +
:<math>b=\pm\sqrt{3}\,</math>
 +
de a második egyenletből ''b'' > 0, így
 +
:<math>z=-1+\sqrt{3}i\,</math>

A lap 2009. október 13., 09:23-kori változata

Komplex számok

Algebrai alak

1. Oldja meg a komplex számok körében az alábbi egyenletet!

\sqrt{2}\frac{|z|}{z}=1-i,\quad\quad\mathbf{C}\ni z=?

Mo. Világos, hogy a z = 0-t kizárhatjuk.

Írjuk fel az ismeretlent algebrai alakban: z = a + b i

\sqrt{2}\frac{\sqrt{a^2+b^2}}{a+bi}=1-i
\sqrt{2}\sqrt{a^2+b^2}=(1-i)(a+bi)
\sqrt{2}\sqrt{a^2+b^2}=a+bi+b-ai

Két komplex szám pontosan akkor egyenlő, ha valós és képzetes részeik egyenlők.

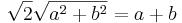
1. \sqrt{2}\sqrt{a^2+b^2}=a+b
2. 0=b-a\,

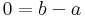
azaz a = b és

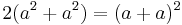
2(a^2+a^2)=(a+a)^2\,
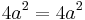
4a^2=4a^2\;
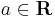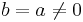
a\in \mathbf{R}, b=a\ne 0

2. Mely komplex számok tesznek egyszerre eleget az alábbi egyenleteknek?

z+\overline{z}=-2,
|z|z=2\sqrt{3}i-2,\quad\quad\mathbf{C}\ni z=?

Mo. Írjuk fel az ismeretlent algebrai alakban: z = a + b i

a+bi+a-bi=-2\,
\sqrt{a^2+b^2}(a+bi)=2\sqrt{3}i-2\,
a=-1\,
-\sqrt{1+b^2}+\sqrt{1+b^2}bi=2\sqrt{3}i-2\,
-\sqrt{1+b^2}=-2\,
1+b^2=4\,
b=\pm\sqrt{3}\,

de a második egyenletből b > 0, így

z=-1+\sqrt{3}i\,
A lap eredeti címe: „http://wiki.math.bme.hu/index.php?title=Szerkeszt%C5%91:Mozo/A1_feladatok_2.&oldid=5586”
Személyes eszközök