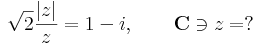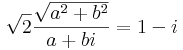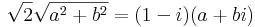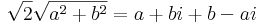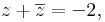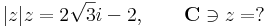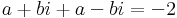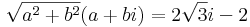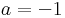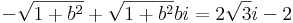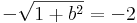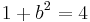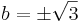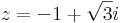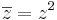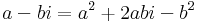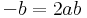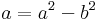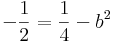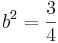Szerkesztő:Mozo/A1 feladatok 2.

Komplex számok

Algebrai alak

1. Oldja meg a komplex számok körében az alábbi egyenletet!

$\sqrt{2}\frac{|z|}{z}=1-i,\quad\quad\mathbf{C}\ni z=?$

Mo. Világos, hogy a z = 0-t kizárhatjuk.

Írjuk fel az ismeretlent algebrai alakban: z = a + b i

$\sqrt{2}\frac{\sqrt{a^2+b^2}}{a+bi}=1-i$

$\sqrt{2}\sqrt{a^2+b^2}=(1-i)(a+bi)$

$\sqrt{2}\sqrt{a^2+b^2}=a+bi+b-ai$

Két komplex szám pontosan akkor egyenlő, ha valós és képzetes részeik egyenlők.

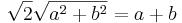
1. $\sqrt{2}\sqrt{a^2+b^2}=a+b$

2. $0=b-a\,$

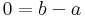
azaz a = b és

$2(a^2+a^2)=(a+a)^2\,$

$4a^2=4a^2\;$

$a\in \mathbf{R}$, $b=a\ne 0$

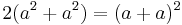
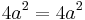
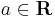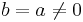
2. Mely komplex számok tesznek egyszerre eleget az alábbi egyenleteknek?

$z+\overline{z}=-2,$

$|z|z=2\sqrt{3}i-2,\quad\quad\mathbf{C}\ni z=?$

Mo. Írjuk fel az ismeretlent algebrai alakban: z = a + b i

$a+bi+a-bi=-2\,$

$\sqrt{a^2+b^2}(a+bi)=2\sqrt{3}i-2\,$

$a=-1\,$

$-\sqrt{1+b^2}+\sqrt{1+b^2}bi=2\sqrt{3}i-2\,$

$-\sqrt{1+b^2}=-2\,$

$1+b^2=4\,$

$b=\pm\sqrt{3}\,$

de a második egyenletből b > 0, így

$z=-1+\sqrt{3}i\,$

3. Mely komplex számok tesznek eleget az alábbi egyenletnek?

$z\overline{z}=z^3,\quad\quad\mathbf{C}\ni z=?$

Mo. z = 0 megoldás. Ha z nem nulla, akkor

$\overline{z}=z^2$

z = a + b i-vel:

$a-bi=a^2+2abi-b^2\,$

$-b=2ab\,$

$a=a^2-b^2\,$

Innen a = -1/2,

$-\frac{1}{2}=\frac{1}{4}-b^2\,$

$b^2=\frac{3}{4}\,$

$b=\pm\frac{\sqrt{3}}{2}\,$

Trigonomertikus alak

4. Oldjuk meg az alábbi egyenletet a komplex számok halmazán!

$z^4=-z,\quad\quad\mathbf{C}\ni z=?$

Mo.