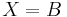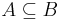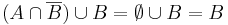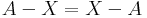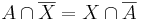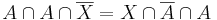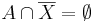Szerkesztő:Mozo/A1 feladatok 2.
Tartalomjegyzék |
Komplex számok
Algebrai alak
1. Oldja meg a komplex számok körében az alábbi egyenletet!
Mo. Világos, hogy a z = 0-t kizárhatjuk.
Írjuk fel az ismeretlent algebrai alakban: z = a + b i
Két komplex szám pontosan akkor egyenlő, ha valós és képzetes részeik egyenlők.
- 1.
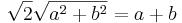
- 2.
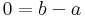
azaz a = b és
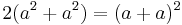
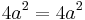
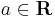 ,
, 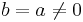
2. Mely komplex számok tesznek egyszerre eleget az alábbi egyenleteknek?
Mo. Írjuk fel az ismeretlent algebrai alakban: z = a + b i
de a második egyenletből b > 0, így
3. Mely komplex számok tesznek eleget az alábbi egyenletnek?
Mo. z = 0 megoldás. Ha z nem nulla, akkor
z = a + b i-vel:
Innen a = -1/2,
Trigonomertikus alak
4. Oldjuk meg az alábbi egyenletet a komplex számok halmazán!
Mo. z = 0 megoldás. Ha z nem nulla, akkor
Egyrészt z = -1, másrészt egységhosszúságú komplex számok a megoldások, hisz
Grafikusan:
5. Oldja meg az alábbi egyenletet a komplex számok halmazán!
Mo. w = z4 új ismeretlennel:
ami a megoldóképlet szerint:
ahol a négyzetgyököt a komplex kétértékű értelemben kell venni.
Ezeknek könnyű előállítani a negyedik gyökeiket. Az abszolút értékek:
![\sqrt[4]{4}=\sqrt{2}](/upload/math/f/2/3/f23db380b0199b416eb98cac80e799d2.png) és
és 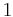 ,
,
így
6. Adja meg a következő kifejezés értékét algebrai alakban!
Mo.
Vektoralgebra
6. Igazoljuk, hogy a derékszögű háromszög derékszögű csúcsát tükrözve a háromszög Thalész-körén lesz.
Mo. A Thalész-kör középpontjából rendere mutassanak a csúcsokba az a, b, c vektorok. Persze a = -b és |a| = |b| = |c| = R.
Kell:
Halmazok
7. 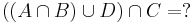 , ha
, ha 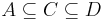 .
.
Mo.
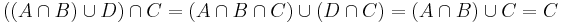 ,
,
8. Oldja meg az alábbi halmazegyenleteket, X-re!
Mo. Legyen a komplementerképzés univerzuma U. Tegyük fel, hogy van megoldás. Eltünik az X komplementer a bal oldalról, ha mindkét oldalt elmetszük X-szel:
ez utóbbi pontosan azt jelenti, hogy X ⊆ B. Emellett a feltétel mellett B-vel a baloldalon "beuniózva":
amiből következik, hogy B ⊆ X és A ⊆ X. Ez azt jelenti, hogy ha van megoldás, akkor az egyértelmű éspedig
Most vizsgáljuk meg a megoldhatóság feltételét. Azt kaptuk, hogy ha van megoldás, akkor A ⊆ X = B, vagyis
De ez elégséges feltétele is a megoldhatóságnak, ugyanis ekkor az X = B helyettesítés kielégíti az egyenletet:
9. Oldja meg az alábbi halmazegyenleteket, X-re!
Mo.
vagyis
Ha van megoldás és bemetszünk mindkét oldalon A-val, akkor
azaz A ⊆ X, de az egyenlet szimmetrikus az A és az X felcserélésére, ezért X ⊆ A is teljesül, amiből X = A, ha van megoldás. Márpedig az egyenletet az X = A kielégíti.
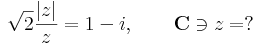
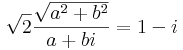
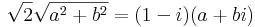
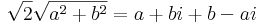
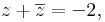
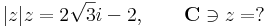
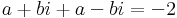
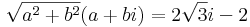
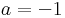
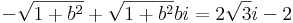
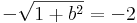
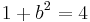
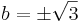
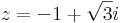

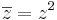
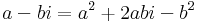
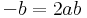
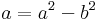
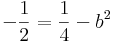
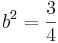
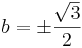

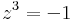
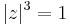
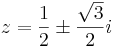
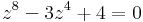
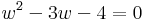
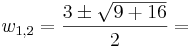
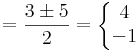
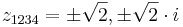
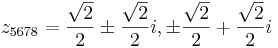
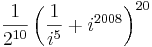
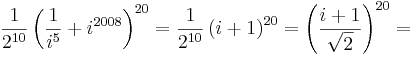
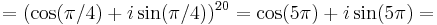
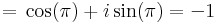
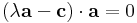
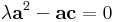
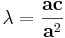
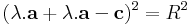
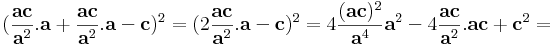
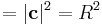
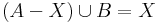
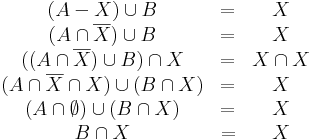
![[\;X =\; ]\quad\quad(A\cap \overline{X}) \cup B =(A\cup B)\cap (\overline{X}\cup B)\supseteq (A\cup B)\cap (\overline{X}\cup X)=(A\cup B)\cap U =A\cup B](/upload/math/2/2/a/22a2065200b5777f3f31a4cfd4bda2b6.png)