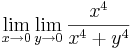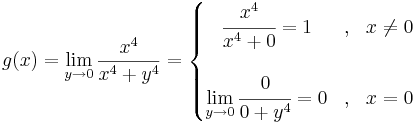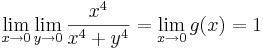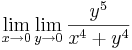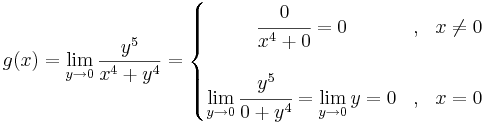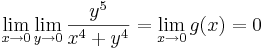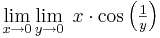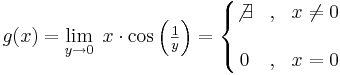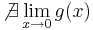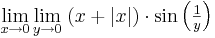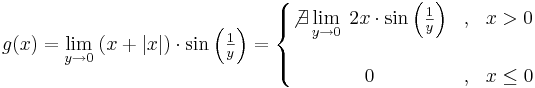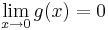Szerkesztő:Mozo/A2 feladatok
Tartalomjegyzék |
Függvényterek
Példa
Legyen L az R-en értelmezett valós függvények következő lineáris altere:
(azaz az exp(2 .), a sin(3
.), a sin(3 .) és a cos(3
.) és a cos(3 .) függvények által kifeszített altér.)
Adjuk meg L bázisát, igazoljuk, hogy
.) függvények által kifeszített altér.)
Adjuk meg L bázisát, igazoljuk, hogy
lineáris operátor és adjuk meg egy mátrixát!
Megoldás
boztosan generátorrendszere L-nek. Lássuk be, hogy B független. Tegyük fel ugyanis, hogy minden x valós számra
Ekkor x = 0-t véve:
illetve x = 2π-t véve is:
mely két egyenletet kivonva
azaz A = 0. Viszont ekkor C = 0-is teljesül és B csak nulla lehet, mert a szinuszfüggvény nem az azonosan nulla. Tehát a fenti egyenlőségnek csak triviális megoldása van A, B, C-ben.
Térjünk rá az operátor linearitására. A deriválás lineáris, a 4-gyel való szorzás lineáris és a leképezések összege lineáris, tehát A lineáris. Adjuk meg a mátrixot! A bázisok képei:
Így
Megjegyezzük, hogy a leképezés lényegében egy x tengely körüli forgatás, majd a tengelyek menti nyújtás. A sajátvektorai: Ae2x, sajátértéke 6.
Iterált határérték
Példa
Megoldás
Példa
Megoldás
Tehát g ≡ 0
Példa
Megoldás
Tehát g egyetlen pontból áll, éspedig a 0-nál 0. Ilyen (egypontú) függvények nincs határértéke:
Példa
Megoldás
Tehát g csak a nemnegatívokon értelmezett és ott 0:
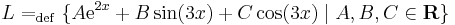
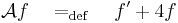
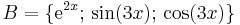
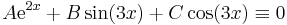
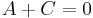
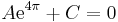
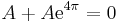
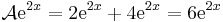
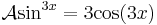

![[\mathcal{A}]=\begin{pmatrix}
6 & 0 & 0 \\
0 & 0 & -3 \\
0 & 3 & 0
\end{pmatrix}=6\cdot\begin{pmatrix}
1 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{pmatrix}+3\cdot\begin{pmatrix}
0 & 0 & 0 \\
0 & 0 & -1 \\
0 & 1 & 0
\end{pmatrix}](/upload/math/a/f/2/af21946b40b58db43824483b6e69cf84.png)