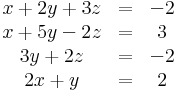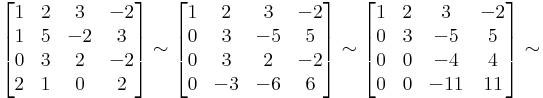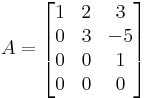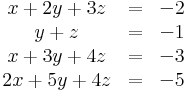Szerkesztő:Mozo/A2 gyakorló feladatok 2

A MathWikiből

(Változatok közti eltérés)

Ugrás: navigáció, keresés

A lap 2008. június 12., 12:23-kori változata

Tartalomjegyzék

1 1. a.
- 1.1 Megoldás
2 1. b.
- 2.1 Megoldás

1. a.

Oldja meg az

$\begin{matrix} x+2y+3z&=&-2 \\ x+5y-2z&=&3 \\ 3y+2z&=&-2 \\ 2x+y&=&2 \end{matrix}$

egyenletrendszert!

Megoldás

Gauss-eliminációval:

$\begin{bmatrix} 1 & 2 & 3 & -2 \\ 1 & 5 & -2 & 3 \\ 0 & 3 & 2 & -2 \\ 2 & 1 & 0 & 2 \\ \end{bmatrix}\sim\begin{bmatrix} 1 & 2 & 3 & -2 \\ 0 & 3 & -5 & 5 \\ 0 & 3 & 2 & -2 \\ 0 & -3 & -6 & 6 \\ \end{bmatrix}\sim\begin{bmatrix} 1 & 2 & 3 & -2 \\ 0 & 3 & -5 & 5 \\ 0 & 0 & -4 & 4 \\ 0 & 0 & -11 & 11 \\ \end{bmatrix}\sim$

$\sim\begin{bmatrix} 1 & 2 & 3 & -2 \\ 0 & 3 & -5 & 5 \\ 0 & 0 & 1 & -1 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix}$

Innen

z = -1,

3y -5 $\cdot$ (-1) = 5, innen y = 0

x = (-2) $\cdot$ 0 + (-3)(-1) -2 = 1

Megjegyzés. Az

$A=\begin{bmatrix} 1 & 2 & 3 \\ 0 & 3 & -5 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{bmatrix}$

mátrix rangja 3 és a kibővített mátrix rangja is ennyi, így az egyenletnek van megoldása (amiről persze maga a "megoldás" is tanúskodik) és ez egyértelmű, mert A magtere a {0} altér. Világos ugyanis, hogy A első három sora független vektorrendszert alkot és így képtérbeli 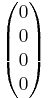$\begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \\ \end{pmatrix}$ vektor csak az 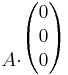$\begin{matrix} \\ \\ A\cdot \\ \end{matrix} \begin{pmatrix} 0 \\ 0 \\ 0 \\ \end{pmatrix}$ szorzatból jön ki.

1. b.

Oldja meg az

$\begin{matrix} x+2y+3z&=&-2 \\ y+z&=&-1 \\ x+3y+4z&=&-3 \\ 2x+5y+4z&=&-5 \end{matrix}$

egyenletrendszert!

Megoldás

$\begin{bmatrix} 1 & 2 & 3 & -2 \\ 0 & 1 & 1 & -1 \\ 1 & 3 & 4 & -3 \\ 2 & 5 & 7 & -5 \\ \end{bmatrix}\sim\begin{bmatrix} 1 & 2 & 3 & -2 \\ 0 & 1 & 1 & -1 \\ 0 & 1 & 1 & -1 \\ 0 & 1 & 1 & -1 \\ \end{bmatrix}\sim\begin{bmatrix} 1 & 2 & 3 & -2 \\ 0 & 1 & 1 & -1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix}$

Innen kétféleképpen mehetünk tovább. Egyrészt az előadáson tanultak szerint egy inhomogén lineáris egyenletrendszer összes megoldását megkapjuk, ha egy megldásához hozzáadjuk a (homogén mátrix) magterét. Egy megoldás:

z = 0,

y -1

x = (-2) $\cdot$ (-1)-3 $\cdot$ 0 - 2 = 0

A magtér

@@ 44. sor: / 44. sor: @@
 & 0 & 0  \\
 \end{bmatrix}</math>
-mátrix rangja 3 és a kibővített mátrix rangja is ennyi, így az egyenletnek van megoldása (amiről persze maga a "megoldás" is tanúskodik) és ez egyértelmű, mert A magtere a {0} altér. Világos ugyanis, hogy ''A'' oszlopai függetlenk és így  képtérbeli <math>\begin{pmatrix}
+mátrix rangja 3 és a kibővített mátrix rangja is ennyi, így az egyenletnek van megoldása (amiről persze maga a "megoldás" is tanúskodik) és ez egyértelmű, mert A magtere a {0} altér. Világos ugyanis, hogy ''A'' első három sora független vektorrendszert alkot és így képtérbeli <math>\begin{pmatrix}
 \\
   \\

Szerkesztő:Mozo/A2 gyakorló feladatok 2

A lap 2008. június 12., 12:23-kori változata

Tartalomjegyzék

1. a.

Megoldás

1. b.

Megoldás

Nézetek

Személyes eszközök

Navigáció

Keresés

Eszközök