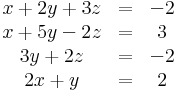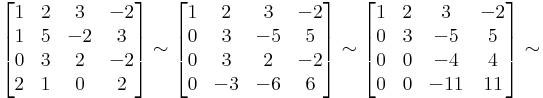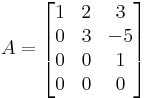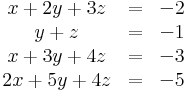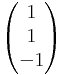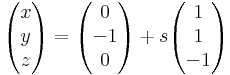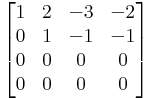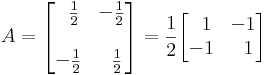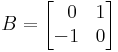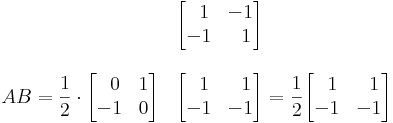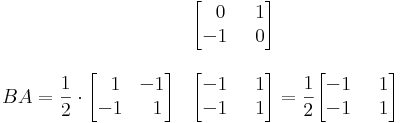Szerkesztő:Mozo/A2 gyakorló feladatok 2

1. a.

Oldja meg az

$\begin{matrix} x+2y+3z&=&-2 \\ x+5y-2z&=&3 \\ 3y+2z&=&-2 \\ 2x+y&=&2 \end{matrix}$

egyenletrendszert!

Megoldás

Gauss-eliminációval:

$\begin{bmatrix} 1 & 2 & 3 & -2 \\ 1 & 5 & -2 & 3 \\ 0 & 3 & 2 & -2 \\ 2 & 1 & 0 & 2 \\ \end{bmatrix}\sim\begin{bmatrix} 1 & 2 & 3 & -2 \\ 0 & 3 & -5 & 5 \\ 0 & 3 & 2 & -2 \\ 0 & -3 & -6 & 6 \\ \end{bmatrix}\sim\begin{bmatrix} 1 & 2 & 3 & -2 \\ 0 & 3 & -5 & 5 \\ 0 & 0 & -4 & 4 \\ 0 & 0 & -11 & 11 \\ \end{bmatrix}\sim$

$\sim\begin{bmatrix} 1 & 2 & 3 & -2 \\ 0 & 3 & -5 & 5 \\ 0 & 0 & 1 & -1 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix}$

Innen

z = -1,

3y -5$\cdot$(-1) = 5, innen y = 0

x = (-2)$\cdot$0 + (-3)(-1) -2 = 1

Megjegyzés. Az

$A=\begin{bmatrix} 1 & 2 & 3 \\ 0 & 3 & -5 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{bmatrix}$

mátrix rangja 3 és a kibővített mátrix rangja is ennyi, így az egyenletnek van megoldása (amiről persze maga a "megoldás" is tanúskodik) és ez egyértelmű, mert A magtere a {0} altér. Világos ugyanis, hogy A oszlopai független vektorrendszert alkotnak és így képtérbeli 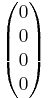$\begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \\ \end{pmatrix}$ vektor csak az 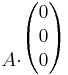$\begin{matrix} \\ \\ A\cdot \\ \end{matrix} \begin{pmatrix} 0 \\ 0 \\ 0 \\ \end{pmatrix}$ szorzatból jön ki.

1. b.

Oldja meg az

$\begin{matrix} x+2y+3z&=&-2 \\ y+z&=&-1 \\ x+3y+4z&=&-3 \\ 2x+5y+4z&=&-5 \end{matrix}$

egyenletrendszert!

Megoldás

$\begin{bmatrix} 1 & 2 & 3 & -2 \\ 0 & 1 & 1 & -1 \\ 1 & 3 & 4 & -3 \\ 2 & 5 & 7 & -5 \\ \end{bmatrix}\sim\begin{bmatrix} 1 & 2 & 3 & -2 \\ 0 & 1 & 1 & -1 \\ 0 & 1 & 1 & -1 \\ 0 & 1 & 1 & -1 \\ \end{bmatrix}\sim\begin{bmatrix} 1 & 2 & 3 & -2 \\ 0 & 1 & 1 & -1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix}$

Innen kétféleképpen mehetünk tovább. Egyrészt az előadáson tanultak szerint egy inhomogén lineáris egyenletrendszer összes megoldását megkapjuk, ha egy megldásához hozzáadjuk a (homogén mátrix) magterét. Egy megoldás:

z = 0,

y -1

x = (-2)$\cdot$(-1)-3$\cdot$ 0 - 2 = 0

A magtér a dimenziótétel miatt egydimenziós, mert a képtér dimenziója a Gauss-eliminációból leolvasva 2, a kiindulási tér pedig 3 dimenziós. Egy magtérbeli vektor a normálalakból, az (1,1,?) alakban keresve az ?=-1, azaz

$\begin{pmatrix} 1 \\ 1 \\ -1 \\ \end{pmatrix}$

vektort adja, ami tényleg A magterben van benne. Ekkor a megoldás:

$\begin{pmatrix} x \\ y \\ z \\ \end{pmatrix}=\begin{pmatrix} 0 \\ -1 \\ 0 \\ \end{pmatrix}+s\begin{pmatrix} 1 \\ 1 \\ -1 \\ \end{pmatrix}$

A másik lehetőség, hogy a harmadik változót paraméternek választjuk, és kifejezzük a változókat az

$\begin{bmatrix} 1 & 2 & -3 & -2 \\ 0 & 1 & -1 & -1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix}$

egyenletrenszerből:

z = t,

y = -t - 1

x = (-2)(-t-1)-3t-2= -t

ami ugyanaz, mint az előző képlet, csak s = -t.

2

Legyen az A operátor R²-ben az y = -x egyenesre vett vetítés, B a 270°-os origó körüli forgatás. Írja fel a leképezések kompozícióinak mátrixát a sztenderd bázisra vonatkozóan. Kommutálnak-e a mártixaik?

Megoldás

Az (1,0) báziselem képe az A által (1/2,-1/2) a (0,1)-é (-1/2,1/2), így:

$A= \begin{bmatrix} \;\;\frac{1}{2} & -\frac{1}{2}\\ & \\ -\frac{1}{2} & \;\;\frac{1}{2} \end{bmatrix}=\frac{1}{2}\begin{bmatrix} \;\;1 & -1\\ -1 & \;\;1 \end{bmatrix}$

Valamint

$B= \begin{bmatrix} \;\;0 & 1\\ -1 & 0 \end{bmatrix}$

Ekkor

$AB=\frac{1}{2}\cdot\begin{matrix} & \begin{bmatrix} \;\;1 & -1\\ -1 & \;\;1 \end{bmatrix} \\ & \\ \begin{bmatrix} \;\;0 & 1\\ -1 & 0 \end{bmatrix} & \begin{bmatrix} \;\;1 & \;\;1\\ -1 & -1 \end{bmatrix} \\ & \\ & \\ & \\ \end{matrix}=\frac{1}{2}\begin{bmatrix} \;\;1 & \;\;1\\ -1 & -1 \end{bmatrix}$

illetve

$BA=\frac{1}{2}\cdot\begin{matrix} & \begin{bmatrix} \;\;0 & \;\;1\\ -1 & \;\;0 \end{bmatrix}\\ & \\ \begin{bmatrix} \;\;1 & -1\\ -1 & \;\;1 \end{bmatrix} & \begin{bmatrix} -1 & \;\;1\\ -1 & \;\;1 \end{bmatrix}\\ & \\ & \\ & \\ \end{matrix}=\frac{1}{2}\begin{bmatrix} -1 & \;\;1\\ -1 & \;\;1 \end{bmatrix}$

És nem kommutálnak.