Szerkesztő:Mozo/A2 gyakorló feladatok 5
Mozo (vitalap | szerkesztései) (→Határérték teljes differenciálhatóság) |
Mozo (vitalap | szerkesztései) (→Határérték teljes differenciálhatóság) |
||
| 23. sor: | 23. sor: | ||
Hol totálisan diferenciálható az | Hol totálisan diferenciálható az | ||
| − | :<math>f(x,y)=\frac{x^3-y^3}{x^2+y | + | :<math>f(x,y)=\frac{x^3-y^3}{x^2+y^2},\qquad (x,y)\ne (0,0),\qquad f(0,0)=0</math> |
függvény? | függvény? | ||
===Mo.=== | ===Mo.=== | ||
| + | Az origón kívül differenciálhatóakból van összetéve a differenciálhatósűgot megőrző módokon. | ||
| + | |||
| + | :<math>f(x,0)=x</math>, azaz <math>\partial_xf(0,0)=1</math> és | ||
| + | :<math>f(0,y)=-y</math>, azaz <math>\partial_yf(0,0)=-1</math> | ||
| + | Ezért a Jacobi-mártix: [1 -1] | ||
| + | :<math>\frac{x^3-y^3-[1\quad -1]\begin{bmatrix}x\\y\end{bmatrix}}{\sqrt{x^2+y^2}}</math> | ||
A lap 2015. április 1., 09:16-kori változata
Tartalomjegyzék |
Topologia
1. Igaz-e bármely végtelen sok zárt halmazból álló halmazrendszerre, hogy unioja nyilt?
2. Igaz-e bármely végtelen sok zárt halmazból álló halmazrendszerre, hogy unioja zárt?
3. Miert zárt a [-1;1] intervallum?
4. Van-e olyan halmaz, mely se nem zárt se nem nyílt, ill. olyan, ami nyílt is és zárt is?
Mo.
1. Nem, ellenpélda: {[-1/n,1/n]|n∈N}, ugyanis U{[-1/n,1/n]|n∈N} = [-1;1], mely nem nyílt, ugyanis a -1 pontnak nincs olyan környezete, mely teljes egészében [-1 ;1]-ben lenne.
2. Nem, ellenpélda: {[-1+1/n,1-1/n]|n∈N}, ugyanis U{[-1+1/n,1-1/n]|n∈N} = (-1;1), ugyanis ha x∈(-1;1), akkor lesz olyan [-1+1/n,1-1/n] mely lefedi x-et. (-1;1) nem zárt ugyanis komplementere: (-∞,-1]U[1;∞) nem nyílt, hisz az 1 nek nincs olyan környezet, mely teljes egészében a halmazban lenne.
3. Mert komplementere a (-∞,-1)U(1;∞) halmaz két nyílt halmaz uniója, ami nyílt.
4. Igen, a [0;1) se nem nyílt, se nem zárt (0 neki, 1 a komplementerének nem belső pontja), és az üres és R nyílt-zárt, mert egymás komplementerei és az üres és R nyílt.
Határérték teljes differenciálhatóság
Hol totálisan diferenciálható az
függvény?
Mo.
Az origón kívül differenciálhatóakból van összetéve a differenciálhatósűgot megőrző módokon.
- f(x,0) = x, azaz
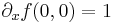 és
és
- f(0,y) = − y, azaz
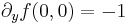
Ezért a Jacobi-mártix: [1 -1]
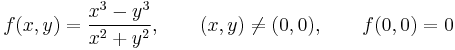
![\frac{x^3-y^3-[1\quad -1]\begin{bmatrix}x\\y\end{bmatrix}}{\sqrt{x^2+y^2}}](/upload/math/3/9/f/39fbace618bd519f2fb69081c2e224e1.png)