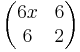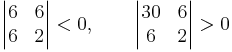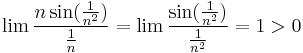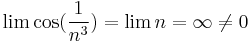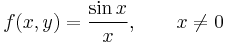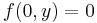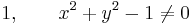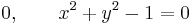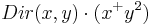Szerkesztő:Mozo/A2 gyakorló feladatok 5
Tartalomjegyzék |
Topologia
1. Igaz-e bármely végtelen sok zárt halmazból álló halmazrendszerre, hogy unioja nyilt?
2. Igaz-e bármely végtelen sok zárt halmazból álló halmazrendszerre, hogy unioja zárt?
3. Miert zárt a [-1;1] intervallum?
4. Van-e olyan halmaz, mely se nem zárt se nem nyílt, ill. olyan, ami nyílt is és zárt is?
Mo.
1. Nem, ellenpélda: {[-1/n,1/n]|n∈N}, ugyanis U{[-1/n,1/n]|n∈N} = [-1;1], mely nem nyílt, ugyanis a -1 pontnak nincs olyan környezete, mely teljes egészében [-1 ;1]-ben lenne.
2. Nem, ellenpélda: {[-1+1/n,1-1/n]|n∈N}, ugyanis U{[-1+1/n,1-1/n]|n∈N} = (-1;1), ugyanis ha x∈(-1;1), akkor lesz olyan [-1+1/n,1-1/n] mely lefedi x-et. (-1;1) nem zárt ugyanis komplementere: (-∞,-1]U[1;∞) nem nyílt, hisz az 1 nek nincs olyan környezet, mely teljes egészében a halmazban lenne.
3. Mert komplementere a (-∞,-1)U(1;∞) halmaz két nyílt halmaz uniója, ami nyílt.
4. Igen, a [0;1) se nem nyílt, se nem zárt (0 neki, 1 a komplementerének nem belső pontja), és az üres és R nyílt-zárt, mert egymás komplementerei és az üres és R nyílt.
Határérték teljes differenciálhatóság
Hol totálisan diferenciálható az
függvény?
Mo.
Az origón kívül differenciálhatóakból van összetéve a differenciálhatósűgot megőrző módokon.
- f(x,0) = x, azaz
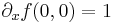 és
és
- f(0,y) = − y, azaz
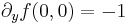
Ezért a Jacobi-mártix: [1 -1]
Ez a függvény az (x,0) pontokban azonosan 0, az (x,-x) pontokban nemnulla konstans, azaz nincs határértéke a (0,0)-ban.
Lokális és tartományi szélsőérték
Legyen
a) Hol és milyen lokális szélsőértéke van?
b) Hol és mekkora az x=0, y=0, y=1-x határolta tartományon a tartományi maximuma és minimuma?
Mo.
Innen y=-3x, x2 − 6x + 5 = 0, azaz x=1; 5, y= rendre -3, -15.
Hesse-mátrix:
Determinánsa az (1;-3) és (5;-15) pontokban rendre
azaz az első pontban maximuma, a másodikban minimuma van.
b) Belül nincs szélsőértéke. A peremen: (x,0), ahol x∈[0,1], akkor x3 + 15x, deriváltja: 2x2 + 15, ennek nincs nullhelye, azaz sz.m.nő: f(0,0)=0, f(1,0)=16. (0,y), ahol y∈[0,1], akkor y2, azaz sz.m.nő [0,1]-en: f(0,0)=0, f(0,1)=1. Az (x,1-x) mentén, ahol x∈[0,1]:
- f(x,1 − x) = x3 + 6x(1 − x) + (1 − x)2 + 15x deriváltja:
- f'(x,1 − x) = 3x2 + 6 − 12x − 2(1 − x) + 15 = 3x2 − 10x + 19 = 3(x − 5 / 3)2 − (25 / 3) + 19 > 0, azaz f(x,1-x) sz. m. nő.
Tehát f(0,0)=0 minimum, f(1,0)=16 maximum.
Konvergens sorok
Konvergensek-e az alábbi sorok?
- a)
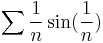
- b)
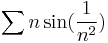
- c)
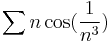
Mo.
a) Igen, 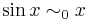 ,
, 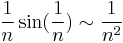 ,és valóban: :
,és valóban: :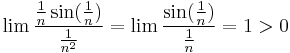 azaz, mivel ∑1/n2 konvergens, ezért az a) sor is az.
azaz, mivel ∑1/n2 konvergens, ezért az a) sor is az.
b) 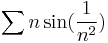 divergens, mert az előző megoldás eleje miatt, azt az alábbiakkal folytatva
divergens, mert az előző megoldás eleje miatt, azt az alábbiakkal folytatva
azaz, mivel ∑1/n divergens, ezért a b) sor is az.
c) A szükséges kritérium alapján, mivel
azaz nem nullához tartanak a tagok, ezért nem lehet c) konvergens, azaz c) divergens. (lim2 cos=1-et használtuk fel a határérték kiszámításakor.)
Integrálhatóság
a) Riemann-integrálható-e az
függvény az [0;1]×[0,1] kockán?
b) Riemann-integrálható-e az
függvény, azaz a 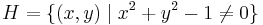 halmaz karakterisztikus függvénye a [-1;1]×[-1;1] kockán?
halmaz karakterisztikus függvénye a [-1;1]×[-1;1] kockán?
c) Riemann-integrálható-e
függvény, az origó középpontú egység sugarú körlapon [0;1]×[0,1] kockán? Itt Dir(x,y) 1, ha (x,y) mindkét komponense racionális, és 0, ha valamelyik irracionális? Hol differenciálható ez a függvény?
Mo.
a) Megszüntethető szakadása van az (0,y) pontok mentén, azaz nullmértékű halmazon és korlátos, tehát integrálható.
b) Korlátos és a körvonal mentén szakad, azaz nullmértékű halmazon, tehát integrálható.
c) racionálisokra a z=x^2+y^2 forgási paraboloid, máshol a 0 függvény. Ez a körlapon az origó kivételével szakad. Ezt a [-1;1]×[-1;1]-re a 0 függvénnyel kiterjesztve nem nullmértékű sok helyen szakad, bár korlátos, azaz nem Riemann-integrálható. A függvény csak az origóban folytonos, de ott (amúgy) differenciálható is.
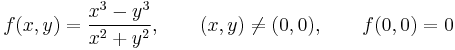
![\frac{\frac{x^3-y^3}{x^2+y^2}-[1\quad -1]\begin{bmatrix}x\\y\end{bmatrix}}{\sqrt{x^2+y^2}}=\frac{\frac{x^3-y^3}{x^2+y^2}-x+y}{\sqrt{x^2+y^2}}=\frac{\frac{x^3-y^3-x^3-xy^2+y^3+yx^2}{x^2+y^2}-x+y}{\sqrt{x^2+y^2}}=](/upload/math/6/1/5/6152931ce0a6bb8f99a96be8ce17d26b.png)
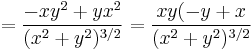
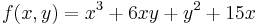
![\nabla f(x,y)=[3x^2+6y+15,\quad 6x+2y]](/upload/math/c/0/4/c04f7a4b1443f41aab02c480e6521bec.png)
![[3x^2+6y+15,\quad 6x+2y]=[0,\quad 0]](/upload/math/5/5/3/553fa18cf3233cff02b94eb2c457a497.png)
![[x^2+2y+5,\quad 3x+y]=[0,\quad 0]](/upload/math/9/c/7/9c784962c3a7b6a72f775ae85d76cbd3.png)