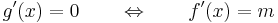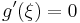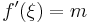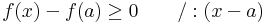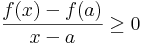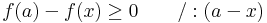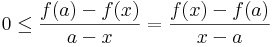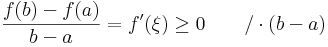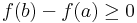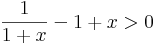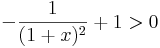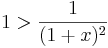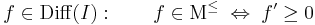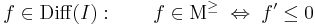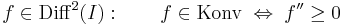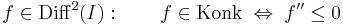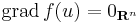Szerkesztő:Mozo/A2 szigorlat 10
Fermat-féle szélsőértéktétel -- Differenciálható függvény belső pontbeli szélsőértéke létezésének szükséges feltétele -- Ha f valós-valós függvény és f differenciálható az u ∈ int Dom(f) pontban és f-nek u-ban lokális szélsőértéke van, akkor
- f'(u) = 0,
Tipikus átvitelielves tétel, hisz a "határérték" létezését tudjuk, csak az értékét kell kiszámolnunk. Tegyük fel, hogy u-ban minimum van. Legyen (δn) az 0-hoz tartó pozitív sorozat, mely minden n-re δn + u, u- δn ∈ Dom(f). Ekkor
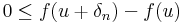 és
és 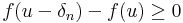
Most az elsőt osszuk le &deta;n-nel, a másodikat -&deta;n-nel. Ekkor:
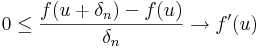 és
és 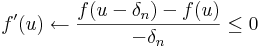
S mivel, ha egy sorozat csupa nemnegatív (nempozitív), akkor a határértéke is ilyen, ezért:
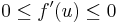 azaz
azaz 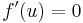
Tétel Lagrange-féle középértéktétel Legyen f: [a,b]  R differenciálható függvény. Ekkor létezik olyan ξ ∈ (a,b), hogy
R differenciálható függvény. Ekkor létezik olyan ξ ∈ (a,b), hogy
Ugyanis, Legyen
Olyan g differenciálható függvény adunk meg, melynek pontosan olyan x helyen van nulla deriváltja, ahol f'(x)=m. Transzformáljuk el az f függvényt az l(x)=m(x-a) függvénnyel:
Ez a függvény egyrészt differenciálható, mert differenciálhatókból van összetéve az azt megőrző módon (speciel, ekkor folytonos is). Másrészt: g(a)=f(a)=g(b). Harmadrészt tetszőleges x ∈ [a,b]-re
A továbbiakban belátjuk, hogy g-nek van az (a,b) nyílton szélsőértéke.
g a Weierstrass-tétel miatt felveszi mindkét típusú extrémumát. Innen esetszétválasztással megyünk tovább.
1) Ha max(g)=f(a) és min(g)=f(a), akkor a függvény konstans, így minden pontja szélsőérték.
2) Ha max(g) és min(g) közül bármelyik nem f(a), akkor ez a valamelyik nem lehet sem a-ban, sem b-ben, mert ott a függvényérték f(a), belül kell, hogy legyen ez a szélsőérték.
Tehát az (a,b)-ben van szélsőértékhely, mondjuk ξ, amire a Fermat-féle szélsőértéktételt alkalmazva kapjuk, hogy
tehát
QED
Feladat. Igazoljuk, hogy intervallumon differenciálható függvény pontosan akkor monoton, ha a deriváltja mindenhol vagy nemnegatív, vagy nempozitív.
Tétel. f:I  R differenciálható. Ekkor a következő két kijelentés ekvivalens egymással:
R differenciálható. Ekkor a következő két kijelentés ekvivalens egymással:
- f monoton növekvő,
- minden x ∈ I-re
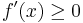
Ugyanis, 1)  2) a < x ∈ I-re: a monotonitásból:
2) a < x ∈ I-re: a monotonitásból:
x < a ∈ I-re: a monotonitásból:
azaz a különbségi-hányados függvény mindenütt nemnegatív (amit úgy nevezünk, hogy a függvény az a-ban lokálisan nő), azaz ennek határértéke sem lehet negatív.
2)  1) minden a < b ∈ I-re:
1) minden a < b ∈ I-re:
azaz f monoton nő.
Tétel. f:I  R differenciálható. Ha minden x ∈ I-re f'(x) > 0f, akkor f szigorúan monoton növekvő.
R differenciálható. Ha minden x ∈ I-re f'(x) > 0f, akkor f szigorúan monoton növekvő.
Ugyanis, inden a < b ∈ I-re:
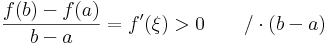
- f(b) − f(a) > 0
azaz f szigorúan monoton nő.
Feladat. Igaz-e?
- Ha f monoton nő, akkor f' nemnegatív.
- Ha f monoton nő, és mindenhol differenciálható, akkor f' nemnegatív.
- Ha f mindenhol differenciálható és f' mindenhol nemnegatív, akkor f monoton nő.
- Ha f intervallumon differenciálható és szigorúan monoton nő, akkor f' pozitív.
Megoldás.
- Ha úgy értjük, hogy mindenhol diffható és f' nemnegatív, akkor nem ha úgy, hogy csak ahol f' létezik, akkor igaz.
- Igen, mert ekkor lokálisan is monoton nő.
- Nem, f(x)=-1/x deriváltja mindenhol létezik, mindenhol nemnegatív és mégsem monoton nő (csak intervallumonként nő)
- Nem, f(x)=x3 szig. mon nő, de 0-ban a derivált 0.
Feladat. Igazoljuk, hogy ha x > 0, akkor f(x) = ln(1+x)-x+1/2x2 > 0!
Megoldás. Mivel 0-ban folytonosan kiterjeszthető, ezért ha a kiterjesztés szigorúan monoton növekvő lenne, akkor fennállna a kijelentés. Ehhez az kell, hogy a derivált (0,+∞)-en pozitív legyen:
A baloldali függvény negativitására abból következtethetünk, hogy szigorúan monoton növekvő a folytonos kiterjesztése (ami létezik, 0-ban 1), amihez az kell, hogy a deriváltja (0,+∞)-en pozitív legyen:
ami fennáll, hiszen ez pont azt mondja, hogy
azaz
- 1 < (1 + x)2
Láttuk a monotonitás differenciális jellemzését:
A szélsőértékre és annak jellegére az első deriváltból a következő módon következtethetünk:
Tétel. -- Elsőderivált próba -- Legyen az f (a,b)  R differenciálható az (a,u)U(u,b) halmazon és folytonos u-ban. Ekkor:
R differenciálható az (a,u)U(u,b) halmazon és folytonos u-ban. Ekkor:
- ha f' < 0 (a,u)-n és f' > 0 (u,b)-n, akkor u-ban minimum van,
- ha f' < 0 (a,u)-n és f' > 0 (u,b)-n, akkor u-ban maximum van,
- ha azonos előjelű mindenhol, akkor biztosan nincs szélsőérték
- ellenkező esetben a próba nem ját sikerrel.
Világos, hogy ehhez kell a monotonitási vizsgálat.
A második derivált vizsgálata A görbületre vonatkozó differenciális feltétel:
A szélsőértékkel analóg fogalom itt az inflexiós pont, mely eleve a differenciális feltétellel definiált: azt mondjuk, hogy az u ∈ I pont inflexiós pontja az 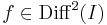 függvénynek, ha abban a pontban a második derivált előjelet vált.
függvénynek, ha abban a pontban a második derivált előjelet vált.
Érdemes még megjegyezni a szélsőértékre vonatkozó másodikderivált próbát, mely lokális abban az értelemben, hogy pusztán csak a második derivált pontbeli értéke a döntő:
Tétel. -- Másodikderivált próba -- Legyen 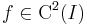 olyan, hogy az u ∈ int(I) pontban f'(u)=0. Ekkor
olyan, hogy az u ∈ int(I) pontban f'(u)=0. Ekkor
- ha f''(u) > 0, akkor u-ban f-nek u-ban lokális minimuma van,
- ha f''(u) < 0, akkor u-ban f-nek u-ban lokális minimuma van,
- más esetekben a próba nem jár sikerrel.
A tétel így, azaz a kétszeri folytonos differenciálhatóság megkövetelésével kimondva világos. Az első esetben u egy környezetében f'' pozitív, azaz f' szig. mon. nő, azaz a f' előjelet vált, így az első derivált próba szerint ott szélsőértéke van (éspedig minimum). A másik eset analóg ezzel.
Tétel - Fermat-féle szélsőértéktétel - Legyen f: Rn  R, u ∈ int Dom(f), f parciálisan differenciálható u-ban.
R, u ∈ int Dom(f), f parciálisan differenciálható u-ban.
- Ha u-ban f-nek (lokális) szélsőértéke van, akkor
U.is: minden i-re az i-edik parciális függvénynek szélsőértéke van ui-ben, így az egyváltozós Fermat-tétel miatt ezeknek a deriváltja ui-ben 0, így a gradiens értéke 0.
Másodikderivált-próba Kétszer differenciálható függvényre vonatkozóan megfogalmazhatjuk a lokális maximum és minimum létezésének elégséges feltételét. Csak a kétváltozós függvényekkel foglalkozunk. Tegyük fel, hogy grad f(u) = 0 és Hf(u) az f Hesse-mátrixa
- ha det Hf(u) > 0 és ∂11f(u) < 0, akkor f-nek u-ban maximuma van
- ha det Hf(u) > 0 és ∂11f(u) > 0, akkor f-nek u-ban minimuma van
- ha det Hf(u) < 0, akkor f-nek biztosan nincs szélsőértéke, ún. nyeregpontja van
- ha det Hf(u) = 0, akkor a próba nem járt sikerrel, azaz további vizsgálatokat igényel annak eldöntése, hogy u szélsőérték hely-e.
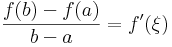
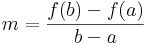
![g(x)=f(x)-m(x-a)\quad\quad(x\in[a,b])](/upload/math/a/3/d/a3d5ab301546f14f71ab5d2316029b1c.png)