Szerkesztő:Mozo/A2 szigorlat 12
- Lásd erről még Serény jegyzetének (ps.gz/dvi) 30., 34-35., 70-72. oldalán.
A V = R2-ben, vagy R3-ban olyan matematikai objektumokat hozunk létre, melyek V minden bázisában felírva egy-egy mátrixszal jellemezhetők, de invariánsak a koordinátarendszer megváltoztatására nézve, azaz mátrixaik egymással vett szorzata (vagy összege, vagy vektorral, számmal vett szorzata) egyenlő a szorzat mátrixával. Rn-ben ilyet könnyen találunk: ezek az L(Rn,Rn)-beli lineáris operátorok:
Definíció. Az L(Rn,Rn)-beli lineáris operátorokat tenzoroknak, vagy másodrendű tenzoroknak nevezzük.
Minthogy a tenzorok maguk is invariánsak, találhatunk velük kapcsolatos további vektor, tenzor vagy skalárinvariánsokat.
Először is megfogalmazzuk, hogy mitől invariáns egy mennyiség. Legyen B és C az n dimenziós V egy-egy bázisa. Legyen T a B-t a C-re váltó koordinátaváltás transzformációja, azaz a
(tehát ez invertálható tenzor). Tudjuk hogy, ha A tetszőleges tenzor, akkor ő egy lineáris leképezés, és emiatt
Ez a tenzorok invariáns tulajdonsága.
Az f(M) ∈ R (M ∈ Mn×n) skalárfüggvényt akkor nevezzük invariánsnak, ha minden B és C bázisra és A tenzorra:
Másként, minden B bázisra, T a B megváltoztató koordinátaváltó transzformációra és A tenzorra
ahol [.] a B-beli koordinátamátrixot jelenti.
Az m(M) ∈ Mn×n (M ∈ Mn×n) mátrixfüggvényt pedig akkor nevezzük invariánsnak, ha minden B és C bázisra és A tenzorra:
azaz ha m az A mátrixával együtt transzformálódik.
Determináns
Vegyük az M  det(M) mátrixleképezést. A determinánsok szorzástétele szerint tetszőleges M és N mátrixra:
det(M) mátrixleképezést. A determinánsok szorzástétele szerint tetszőleges M és N mátrixra:
Emiatt ha A az A tenzor egy mátrixa és T a koordinátaváltó-mátrix, akkor:
Hiszen T-1T = I az egységmátrix.
Értelmes tehát az A tenzor determinánsának értelmezése úgy, hogy det(A) az A tetszőleges mátrixának determinánsa.
Nyom, trace, spur
Vegyük a következő mátrix leképezést:
azaz a mátrixok főátlóbeli elemeinek összegét. Ez is invariáns, melyet a következőkkel bizonyíthatunk. Először is belátjuk a spur szimmetrikus tulajdonságát. Tetszőleges A, B mátrixra Sp(AB) = Sp(BA). Tudjuk, hogy két mátrix szorzata a következőképpen definiált:
ezért:
Ez a képlet azt mondja, hogy "spur alatt a mátrixok kommutálnak". Az invariancia pedig:
Ez a mennyiség tehát az A tenzor egy skalárinvariánsa.
Szimmetrikus és antiszimmetrikus tenzorok
Vegyük az A lineáris leképezést és ennek az S sztenderd bázisbeli mátrixát A-t. Ekkor világos, hogy az AT transzponált mátrixszal történő AT[v]S szorzás egy lineáris leképezés, tehát tenzor, tenzortranszponálás definíciója tehát az, hogy minden A tenzorhoz hozzárendeljük a következő lineáris leképezést:
ahol  a mátrixszorzás.
a mátrixszorzás.
Ám, ez nem minden bázisban viselkedik úgy, ahogy azt a transzponálástól elvárjuk, azaz ha B egy tetszőleges bázis, akkor az [A]BT már nem feltétlejül a T-1 ATT mátrix, ahogy azt várnánk. Ellenben ortonormált bázisokra és a köztük váltó ortogonális transzformációkra már igen. Ezután a tárgyalást csak ortonormált (azaz páronként merőleges, egységhosszúságú bázisvektorú) bázisokra és az ezek között váltó OT = O-1 egyenlőségnek eleget tévő távolságtartó vagy másként ortogonális transzformációkra szorítkozunk.
Igaz az alábbi invariancia-tulajdonság. Ha B tetszőleges ortonormált bázis, [A]B=A és OT = O-1, akkor
(Felhasználtuk a szorzat transzponálásának (AB)T= BTAT szabályát -- nemdebár a mátrixszorzás nem kommutatív.) Tehát a sztenderd bázisban definiált transzponálás minden ortonormált bázisban transzponálás lesz, így ha csak ezekre szorítkozunk, akkor a AT fenti definíciója invariáns leképezést ad meg.
Lényeges tehát, hogy transzponálást, szimmetria és antiszimmetria vizsgálatokat a tenzorok tekintetében most úgy végezünk, hogy tudatában vagyunk annak, hogy eközben a hagyományos, geometriai |a||b|cos γ definíciójú skaláris szorzást használjuk (illetve ennek komponensenkénti változatát). Ezért nevezzük ezeket néha geometriai tenzoroknak.
Az S tenzor szimmetrikus, ha minden ortonormált bázisban a mátrixa szimmetrikus mátrix. Igaz az, hogy S pontosan akkor szimmetrikus, ha minden u, v vektorra
- u
 (Sv)=v
(Sv)=v (Su),
(Su),
ahol  a skaláris szorzás.
a skaláris szorzás.
Az A tenzor antiszimmetrikus, ha minden ortonormált bázisban a mátrixa antiszimmetrikus mátrix. Igaz az, hogy A pontosan akkor antiszimmetrikus, ha minden u, v vektorra
- u
 (Av)=-v
(Av)=-v (Au),
(Au),
ahol  a skaláris szorzás.
a skaláris szorzás.
Bármely T tenzor egyértélműen előáll S + A alakban, ahol S szimmetrikus, A pedig antiszimmetrikus, éspedig:
Két fontos tétel:
Tétel -- Ha A ∈R3 (illetve R2 ) antiszimmetrikus, akkor létezik olyan a vektor (vagy a skalár), hogy minden v vektorra:
a-t (ill. a-t) az A vektorinvariánsának nevezzük (bár a síkon ez skalár). A tételt elég a sztenderd bázisban igazolni, ott az a×( . ) opertátorral, azonos így A ez az operátor.
Főtengelyétel -- Ha S ∈Rn szimmetrikus, akkor minden sajátértéke valós és létezik a sajátvektorokból álló B ortonormált bázis, amiben S főtengelyre transzformálható, azaz diagonális és az elemei az S sajátértékei:
Ez nehéz, de fontos tétel.

![[\mathbf{A}]_C=[\mathbf{T}^{-1}]_B[\mathbf{A}]_B[\mathbf{T}]_B\,](/upload/math/1/e/8/1e86f5ac6238920be02735a4995475fc.png)
![f([\mathbf{A}]_C)=f([\mathbf{A}]_B)\,](/upload/math/4/1/3/413f64190dcf29a18a75473d47f8e612.png)
![f([\mathbf{A}])=f([\mathbf{T}^{-1}][\mathbf{A}][\mathbf{T}])\,](/upload/math/5/b/6/5b60873191e7c52251cbcbd7f4a2b39e.png)
![m([\mathbf{A}]_C)=[\mathbf{T}^{-1}]m([\mathbf{A}]_B)[\mathbf{T}])\,](/upload/math/3/a/3/3a3bd86297790dd047e40a881ce829b3.png)
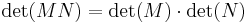
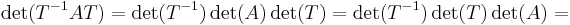
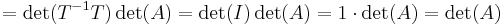
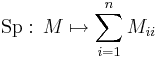
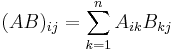
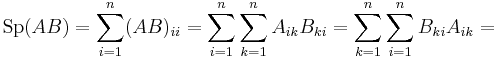
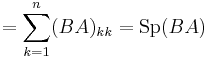
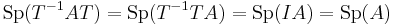
![\mathbf{A}^{\mathrm{T}}\mathbf{v}=[\mathbf{A}]_S^T\cdot [\mathbf{v}]_S\,](/upload/math/0/a/3/0a3e3168846ab0faa0d695ff3dc4f954.png)
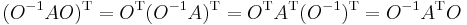
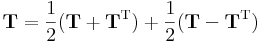
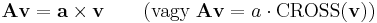
![[\mathbf{S}]_{\{\mathbf{v}_1,...,\mathbf{v}_n\}}=\begin{pmatrix}\lambda_1& 0& 0\\
0& \ddots& 0\\
0 & 0& \lambda_n\end{pmatrix}](/upload/math/2/b/6/2b6d68afeb211967e07984838ae5f4a1.png)