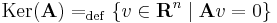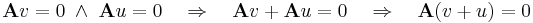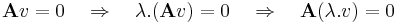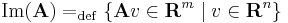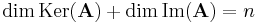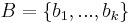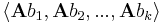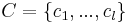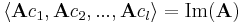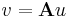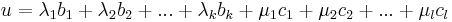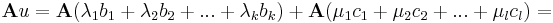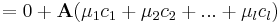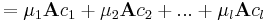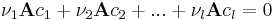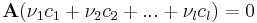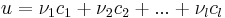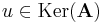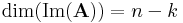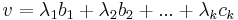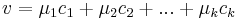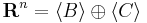Szerkesztő:Mozo/A2 szigorlat 16
A dimenziótétel az lineáris leképezések magterének és képterének dimenziója közötti szoros (kiegészítő jellegű) kapcsolatra mutat rá. Most csak az 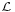 (Rn;Rm) leképezéseket vizsgáljuk (a tétel bármely végesdimenziós vektortérből tetszőleges vektortérbe menő lineáris függvényre is igaz.)
(Rn;Rm) leképezéseket vizsgáljuk (a tétel bármely végesdimenziós vektortérből tetszőleges vektortérbe menő lineáris függvényre is igaz.)
Magtér
Az A : Rn  Rm lineáris leképezés magtere:
Rm lineáris leképezés magtere:
világos, hogy ez altér. Ugyanis altér jelemzhető úgy, mint olyan részhalmaz a térben, mely zárt az összeadásra és a skalárral történő szorzásra. De Ker(A) ilyen, mert tetszőleges u, v vektorra
és
Bázisát (Rn-ben) például az A leképezés [A] mátrixának Gauss-eliminációjával és az [A]x=0 homogén egyenletrendszer megoldásával nyerhetünk (példa itt).
Képtér
Az A : Rn  Rm lineáris leképezés képtere:
Rm lineáris leképezés képtere:
világos, hogy ez altér. Ugyanis alkalmas v és u vektorokkal:
és
Bázisát (Rn-ben) például úgy nyerünk, hogy a A leképezés [A] mátrixának oszlopvektorai közül Gauss-eliminációval kiválasztjuk a legtöbb vektort tartalmazó lineárisan független rendszert (példa itt).
Tétel és bizonyítás
Dimenziótétel. Ha A : Rn  Rm lineáris leképezés, akkor
Rm lineáris leképezés, akkor
Bizonyítás. Ha vesszük Ker(A) egy
bázisát (Ker(A) dimenziója tehát k) akkor világos, hogy a báziselemek képei által kifeszített
altér az Rm-beli triviális {0} altér. Világos, hogy ha veszük egy Ker(A)-n kívüli c vektort, akkor ez már nem képeződhet a {0}-ba. Megfogalmazhatjuk tehát azt a sejtést, hogy ha B-t kibővítíjük Rn bázisává, mondjuk a
független vektorrendszerrel, akkor C elemeinek képei Im(A) bázisát fogja adni. Ezt fogjuk igazolni, azaz hogy
és ami a tétel állítását igazolja: Im(A) dimenziója pont l.
1. Először belátjuk, hogy { Ac1, Ac2, ...,Acl } generátorrendszere Im(A)-nak. Legyen
Mivel B + C bázisa Rn-nek, ezért u előáll (egyértelmű módon)
alakban. De u képében a B-beliekkel előállíthatók a {0}-ba mennek, így már a C-ből jövő képek is előállítják Au-t:
2. Belátjuk, hogy { Ac1, Ac2, ...,Acl } független vektorrendszer is, tehát dimenziója l.
Tegyük fel, hogy vannak ν1, ν2, ...,νl számok, melyekkel
A függetlenséghez az kell, hogy ν1, ν2, ...,νl-k mind nullák legyenek. Természetesen a bal oldalon kiemelhetünk A-t, tehát:
Ez viszont pontosan azt jelenti, hogy ha az
rövidítéshez folyamodunk, akkor
azaz az u vektor B-beli elemekkel is és C-beli elemekkel is előállítható. De ez csak úgy lehet, hogy u=0, ami pedig csak akkor van, ha a ν1, ν2, ...,νl számok mind nullák.
Mindez azt jelenti, hogy { Ac1, Ac2, ...,Acl } bázis, amiből következik, hogy az általa kifeszített altér dimenziója l. De a kifeszített altér pont Im(A), így azt kaptuk, hogy
vagyis, amit be akartunk látni.
Megjegyzés. Világos, hogy a fenti bizonyításban a B által generál altér és a C által generált altér közös része a {0} (vagyis csak a 0-t állítják elő mindeketten). Ugyanis, ha lenne v ≠ 0, hogy
és közben
akkor mindkét egyenletben a skalárok között lenne nemnulla, és a két egyenletet kivonva egymásból hpnánk, hogy a 0 vektor előáll olyan B és C-beli elemek lineáris kombinációjaként, ahol az együtthatók között van nemnulla. Ez viszont az jelentené, hogy B + C nem független rendszer (holott B + C a B egy kibővítése az Rn bázisává).
Ilyenkor azt mondjuk, hogy a Rn vektorteret előállítottuk a B által kifeszített és a C által kifeszített alterek direkt összegeként: