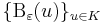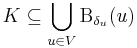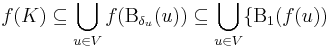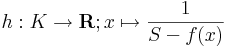Szerkesztő:Mozo/A2 szigorlat 5
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) |
||
| 7. sor: | 7. sor: | ||
'''Tétel''' – ''Weierstrass-féle minimum-maximum-elv'' – Korlátos és zárt intervallumon értelmezett folytonos függvény felveszi abszolút minimumát és maximumát. | '''Tétel''' – ''Weierstrass-féle minimum-maximum-elv'' – Korlátos és zárt intervallumon értelmezett folytonos függvény felveszi abszolút minimumát és maximumát. | ||
| − | Az alábbiakban felhasználjuk a kompaktság fogalmát | + | Az alábbiakban felhasználjuk a kompaktság fogalmát. |
| − | (''Kompakt'' egy ''K'' halmaz, ha minden nyílt halmazrendszerből, melynek uniója lefedi ''K''-t kiválasztható véges sok nyílt halmaz is, melyek véges uniója még mindig lefedi ''K''-t | + | (''Kompakt'' egy ''K'' halmaz, ha minden nyílt halmazrendszerből, melynek uniója lefedi ''K''-t kiválasztható véges sok nyílt halmaz is, melyek véges uniója még mindig lefedi ''K''-t.) |
| − | + | ||
| − | + | ||
'''Tétel''' (''Weierstrass'') Valós értékű, kompakt halmazon folytonos függvény felveszi minimumát és maximumát. | '''Tétel''' (''Weierstrass'') Valós értékű, kompakt halmazon folytonos függvény felveszi minimumát és maximumát. | ||
| − | : | + | :Azaz ha ''K''⊆'''R'''<sup>N</sup> kompakt és ''f'' ∈ C(''K'','''R'''), akkor sup(''f''), inf(''f'') ∈ Ran(''f'') |
| − | ''Bizonyítás.'' | + | ''Bizonyítás.'' 1) Először belátjuk, hogy kompakt halmazon folytonos függvény korlátos. Legyen ugyanis az ε=1 és ''f'' értelmezési tartománya ''K''. A folytonosság miatt ''K'' minden ''u'' eleméhez létezik δ(''u'') pozitív szám, hogy ''f'' a B<sub>δ</sub>(''u'') környezeten belül mindvégig az (''f''(''u'')-1;,''f''(''u'')+1) intervallumon belül marad. Ekkor a nyílt halmazokból álló |
| + | :<math>\{\mathrm{B}_{\varepsilon}(u)\}_{u\in K}\,</math> | ||
| + | rendszer lefedi ''K''-t, vagyis a Heine-Borel-tétel miatt már ebből véges sok is lefedi, azaz létezik ''V'' ⊆ ''K'' véges, hogy | ||
| + | :<math>K\subseteq\bigcup\limits_{u\in V}\mathrm{B}_{\delta_{u}}(u)\,</math> | ||
| + | Ezek képei lefedik Ran(f)-et: | ||
| + | :<math>f(K)\subseteq\bigcup\limits_{u\in V}f(\mathrm{B}_{\delta_{u}}(u))\subseteq\bigcup\limits_{u\in V}\{\mathrm{B}_{1}(f(u))\,</math> | ||
| + | Ez utóbbi a folytonosság miatt, tehát ''f'' képét véges sok korlátos intervallum lefedi, azaz korlátos. | ||
| − | + | 2) Belátjuk, hogy ''f'' felveszi a szuprémumát (és ugyanígy az infimumát is). Legyen ''S'' := sup(''f'') (azaz ''f'' értékkészletének legkisebb felső korlátja). Ekkor a ''g'' : ''K'' <math>\to</math> '''R''', ''x'' <math>\mapsto</math> ''S''-''f''(''x'') függvény nemnegatív értékeket vesz föl. Ha ''f'' nem venné fel a szuprémumát, akkor ''g'' pozitív lenne. Ekkor értelmezhető lenne a | |
| + | :<math>h:K\to\mathbf{R};x\mapsto \frac{1}{S-f(x)}</math> | ||
| + | függvény. <math>h</math> mert folytonos függvényekből van folytonosságot megőrző módon összetéve. Az 1) pont szerint korlátos is, ami azonban ellentmond annak, hogy ''S'' a szuprémum. Ugyanis S = sup Ran(''f'') azt jelenti, hogy minden 1/n alakú számra van <math>x_n</math> ∈ ''K'', hogy <math>|S - f(x_n)|<1/n</math>, azaz van olyan ''K''-beli <math>x_n</math> sorozat, melynek képsorozata ''h'' által a végtelenbe tart, azaz ''h'' nem korlátos. | ||
| + | |||
| + | '''Tétel''' (''Bolzano'') Összefüggő halmaz folytonos képe összefüggő. | ||
| + | :(Ha ''f'' ∈ C('''R'''<sup>n</sup>,'''R'''<sup>m</sup>), Dom(''f'') ívszerűen összefüggő, akkor Ran(''f'') is ívszerűen összefüggő.) | ||
| − | + | ''Bizonyítás.'' Az ívszerű összefüggőségből és a folytonos függvények kompozíciójára vonatkozó tételből. | |
| − | + | ||
| − | + | ||
A lap 2015. május 24., 19:50-kori változata
Tétel – Bolzano-tétel – Intervallumon értelmezett, negatív és pozitív értékeket is felveő folytonos függvénynek van zérushelye.
a Bolzano-tételt még olymódon is szokás kimondani, hogy
- intervallumon értelmezett folytonos függvény két függvényértéke között minden értéket fölvesz
melyet Darboux-tulajdonságnak neveznek. A Bolzano-tétel lényegében azt mondja ki, hogy az intervallumon folytonos függvények Darboux-tulajdonságúak. Megjegyezzük, hogy a Darboux-tétel pedig azt mondja ki, hogy az intervallumon differenciálható függvények deriváltfüggvénye Darboux-tulajdonságú.
Tétel – Weierstrass-féle minimum-maximum-elv – Korlátos és zárt intervallumon értelmezett folytonos függvény felveszi abszolút minimumát és maximumát.
Az alábbiakban felhasználjuk a kompaktság fogalmát.
(Kompakt egy K halmaz, ha minden nyílt halmazrendszerből, melynek uniója lefedi K-t kiválasztható véges sok nyílt halmaz is, melyek véges uniója még mindig lefedi K-t.)
Tétel (Weierstrass) Valós értékű, kompakt halmazon folytonos függvény felveszi minimumát és maximumát.
- Azaz ha K⊆RN kompakt és f ∈ C(K,R), akkor sup(f), inf(f) ∈ Ran(f)
Bizonyítás. 1) Először belátjuk, hogy kompakt halmazon folytonos függvény korlátos. Legyen ugyanis az ε=1 és f értelmezési tartománya K. A folytonosság miatt K minden u eleméhez létezik δ(u) pozitív szám, hogy f a Bδ(u) környezeten belül mindvégig az (f(u)-1;,f(u)+1) intervallumon belül marad. Ekkor a nyílt halmazokból álló
rendszer lefedi K-t, vagyis a Heine-Borel-tétel miatt már ebből véges sok is lefedi, azaz létezik V ⊆ K véges, hogy
Ezek képei lefedik Ran(f)-et:
Ez utóbbi a folytonosság miatt, tehát f képét véges sok korlátos intervallum lefedi, azaz korlátos.
2) Belátjuk, hogy f felveszi a szuprémumát (és ugyanígy az infimumát is). Legyen S := sup(f) (azaz f értékkészletének legkisebb felső korlátja). Ekkor a g : K 
R, x 
S-f(x) függvény nemnegatív értékeket vesz föl. Ha f nem venné fel a szuprémumát, akkor g pozitív lenne. Ekkor értelmezhető lenne a
függvény. h mert folytonos függvényekből van folytonosságot megőrző módon összetéve. Az 1) pont szerint korlátos is, ami azonban ellentmond annak, hogy S a szuprémum. Ugyanis S = sup Ran(f) azt jelenti, hogy minden 1/n alakú számra van xn ∈ K, hogy | S − f(xn) | < 1 / n, azaz van olyan K-beli xn sorozat, melynek képsorozata h által a végtelenbe tart, azaz h nem korlátos.
Tétel (Bolzano) Összefüggő halmaz folytonos képe összefüggő.
- (Ha f ∈ C(Rn,Rm), Dom(f) ívszerűen összefüggő, akkor Ran(f) is ívszerűen összefüggő.)
Bizonyítás. Az ívszerű összefüggőségből és a folytonos függvények kompozíciójára vonatkozó tételből.
