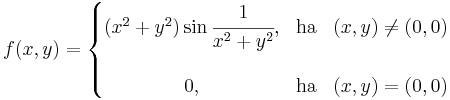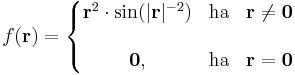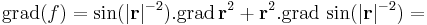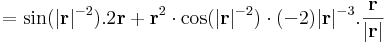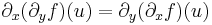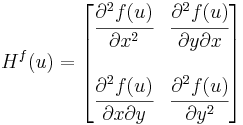Szerkesztő:Mozo/A2 szigorlat 7
Definíció. Legyen f: Rn  R, u ∈ int Dom(f). Azt mondjuk, hogy f parciálisan differenciálható az u pontban a xi változó szerint, ha az
R, u ∈ int Dom(f). Azt mondjuk, hogy f parciálisan differenciálható az u pontban a xi változó szerint, ha az
egyváltozós valós függvény differenciálható az ui pontban. Ekkor a fenti függvény ui-beli deriváltját
jelöli.
Példa:
Parciálisan deriválható-e az
a (0,0)-ban?
Parciálisan deriválható-e az
a (0,0)-ban?
Definíció. Legyen f: Rn  Rm és u ∈ int Dom(f). Azt mondjuk, hogy f differenciálható az u pontban, ha létezik olyan A: Rn
Rm és u ∈ int Dom(f). Azt mondjuk, hogy f differenciálható az u pontban, ha létezik olyan A: Rn  Rm lineáris leképezés, hogy
Rm lineáris leképezés, hogy
Ekkor A egyértelmű és az f leképezés u-bent beli differenciáljának nevezzük és df(u)-val vagy Df(u)-val jelöljük. Ezt a fogalmat néha teljes differenciálnak, totális differenciálnak vagy Fréchet-deriváltnak is mondjuk.
Megjegyzés. A fenti határérték 0 volta egyenértékű a következő kijelentéssel. Létezik A: Rn  Rm lineáris leképezés és ε: Dom(f)
Rm lineáris leképezés és ε: Dom(f)  Rm függvény, melyre:
Rm függvény, melyre:
- ε folytonos u-ban és ε(u)=0, továbbá
minden x ∈ Dom(f)-re:
Megjegyzés. Azt, hogy A egyértelmű, a következőkkel bizonyíthatjuk. Legyen A és B is a mondott tulajdonságú, azaz létezzenek ε és η az u-ban eltűnő és ott folytonos Dom(f)-en értelmezett függvények, melyekre teljesül, hogy minden x ∈ Dom(f)-re
ezeket kivonva egymásból és használva minden x-re:
így minden x = u + ty értékre is az azonosan nullát kapjuk, ha t pozitív szám, y pedig rögzített nemnulla vektor, azaz minden t-re
az azonosan 0 függény határértéke t 0 esetén szintén nulla:
0 esetén szintén nulla:
hiszen t-t kiemelhetünk és egyszerűsíthetünk és t 0 esetén
ε és η nullává válik.
Ez viszont pont azt jelenti, hogy a két lineáris operátor azonosan egyenlő.
0 esetén
ε és η nullává válik.
Ez viszont pont azt jelenti, hogy a két lineáris operátor azonosan egyenlő.
Jacobi-mátrix A df(u) lineáris leképezés (e1,e2,...,en) szetenderd bázisbeli mátrixa legyen: [df(u)] = A. Vizsgáljuk mibe viszi a bázisokat df(u) leképezés!
Írjuk fel a definíciót, de az e1 egységvektor mentén tartsunk u-hoz: x = u + te1. Ekkor
ami azért hasznos, mert a
alakból kiemelhetó t:
azaz
vagyis f koordinátafüggvényeinek az első változó szerinti parciális deriváltja az u pontban. A többi oszlopvektor ugyanígy:
amelyet Jacobi-mátrixnak nevezünk.
Következmény. Tehát. ha f totálisan differenciálható, akkor parciálisan is differenciálható és a differenciál sztenderd bázisbeli mátrixa a Jacobi-mátrix.
Azaz:
- teljes differenciálhatóság
 parciális differenciálhatóság
parciális differenciálhatóság
de ez fordítva már nem igaz:
- parciális differenciálhatóság
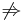 teljes differenciálhatóság
teljes differenciálhatóság
Tétel. Ha az f:Rn ⊃ Rm függvény minden parciális deriváltfüggvénye létezik az u egy környezetében és u-ban a parciális deriváltak folytonosak, akkor u-ban f differenciálható. (Sőt, folytonosan differenciálható.)
Rm függvény minden parciális deriváltfüggvénye létezik az u egy környezetében és u-ban a parciális deriváltak folytonosak, akkor u-ban f differenciálható. (Sőt, folytonosan differenciálható.)
Világos, hogy a parciális deriváltak folytonossága szükséges a fenti tételben.
A differenciálhatóság azonban nem elég ahhoz, hogy a parciális deriváltak folytonosak legyenek.
Az
differenciálható, hiszen ez az
függvény és r ≠ 0-ban:
és grad f nem korlátos. Ez persze a parciális deriváltakon is meglátszik: azok sem korlátosak.
Tétel. (Young-tétel) Ha a másodrendű parciláis deriváltak léteznek az u egy környezetében és folytonosak az u pontban, akkor az u-beli vegyes másodrendű parciláis deriváltak egyenlőek:
Azaz az alábbi, úgy nevezett Hesse-mátrix szimmetrikus:
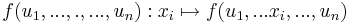
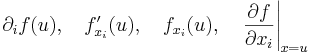
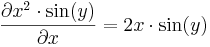
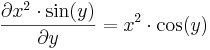
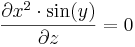
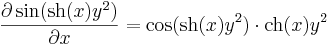
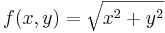
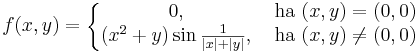
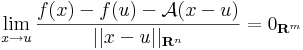
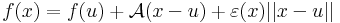
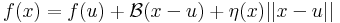
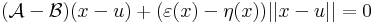
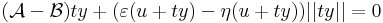
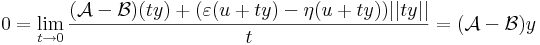
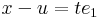
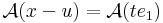
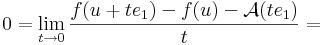
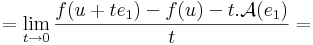
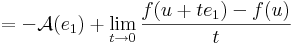
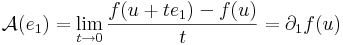
![[\mathrm{d}f(u)]=\mathbf{J}^f(u)=\begin{bmatrix}
\partial_1 f_1(u) & \partial_2 f_1(u) & \dots & \partial_n f_1(u)\\
\partial_1 f_2(u) & \partial_2 f_2(u) & \dots & \partial_n f_2(u)\\
\vdots & \vdots & \ddots & \vdots \\
\partial_1 f_m(u) & \partial_2 f_m(u) & \dots & \partial_n f_m(u)\\
\end{bmatrix}](/upload/math/b/c/8/bc8c1cf3c3d6f5032a7858552cc82a3a.png)