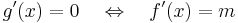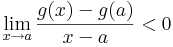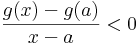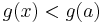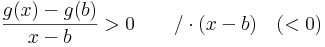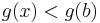Szerkesztő:Mozo/A2 szigorlat 8
Deriváltak, differenciálási szabályok
Definíció. Az f: R⊃ R függvény deriváltfüggvényén értjük a
R függvény deriváltfüggvényén értjük a
Linearitás
- A hozzáadott konstans szabálya:
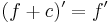
- A konstans szorzó szabálya:
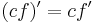
- Linearitás:
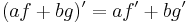
Szorzat és hányados
Összetett függvény
L'Hospital-szabályok
Tétel -- Gyenge L'Hospital-szabály -- Legyenek f és g: A  R valós-valós függvények, u ∈ A ∩ A ', f(u)=g(u)=0, mindkettő differenciálható u-ban és g'(u) ≠ 0. Ekkor létezik a limu(f/g), és
R valós-valós függvények, u ∈ A ∩ A ', f(u)=g(u)=0, mindkettő differenciálható u-ban és g'(u) ≠ 0. Ekkor létezik a limu(f/g), és
Ugyanis,' írjuk fel az 1. definíciónak megfelelően a határértéket. Létezik az u-hoz olyan ε, η: A  R, hogy minden x ∈ A ∩ Dom(f/g)-ra
R, hogy minden x ∈ A ∩ Dom(f/g)-ra
és ∃limuε=ε(u)=0, ∃limuη=η(u)=0. Emiatt és f(u)=g(u)=0 miatt
Aminek a határéttéke, ha x tart u-hoz a kívánt hányados, amennyiben ellenőrizük, hogy g'(u) + η nem lesz nulla egy elég szűk környzeteben. Ekkor ugyanis a hányadosnak nem lenne értelme. Nos, |η| egy elég kis környzetben a nulla |g'(u)|/2 sugarú környzetében lesz, így ez a veszély nem fenyeget.
Amikor nem működik az ismételt L'Hospitálás
Amikor nem működik az ismételt L'Hospitálás
A derivált szakadásai, Darboux-tétel Intervallumon deriválható függvény deriváltjának nem lehet megszüntethető szakadása. (Ellenben lehet korlátos másodfajú és a végtelen másodfajú szakadása.)
Állítás. Ha f:[a,b]  R folytonos a-ban, differenciálható a nyílton és létezik a derivált határértéke a-ban és ez véges szám, akkor f-nek létezik a deriváltja a-ban (és a deriváltja a lima f' szám).
R folytonos a-ban, differenciálható a nyílton és létezik a derivált határértéke a-ban és ez véges szám, akkor f-nek létezik a deriváltja a-ban (és a deriváltja a lima f' szám).
Bizonyítás. Ez az erős L'Hospital-tétel következménye. Tekintsük a különbségi hányados függvényt, legyen a L'H-beli számláló az x  f(x)-f(a), a nevező az x
f(x)-f(a), a nevező az x  x-a. Világos, hogy a-ban 0/0 alakú, így alkalmazható a L'H-szabály. Ekkor
x-a. Világos, hogy a-ban 0/0 alakú, így alkalmazható a L'H-szabály. Ekkor
azaz létezik a pontbeli derivált és ez a derivált határértéke. QED
A deriváltfüggvénynek nem lehet ugrása sem:
Tétel – Darboux-tétel – Ha f:I  R differenciálható, akkor f' Darboux-tulajdonságú (két deriváltérték között a deriváltfüggvény minden értéket fölvesz).
R differenciálható, akkor f' Darboux-tulajdonságú (két deriváltérték között a deriváltfüggvény minden értéket fölvesz).
Bizonyítás. Legyen [a,b] ⊆ I és tegyük fel, hogy f'(a) < m < f'(b) tetszőlegesen rögzített m-re. Belátjuk, hogy van olyan ξ ∈ (a,b), hogy f'(ξ) = m. Transzformáljuk el a függvényt, vonjuk ki belőle az x  mx lineárist:
mx lineárist:
g differenciálható, és olyan, hogy tetszőleges x-re:
A feladat tehát, hogy keressünk zérushelyet g'-nek. Ehhez elég, ha találunk g értelmezési tartományának belsejében szélsőértéket, mert akkor a Fermat-féle szélsőértéktétel miatt ott a derivált nulla lesz. Az [a,b] zárton a folytonos g a Weierstrass-tétel miatt felveszi a szélsőértékeit. Tehát készen vagyunk, amennyiben létezik szélsőérték az (a,b) nyílton. A továbbiakban ezt bizonyítjuk.
Vizsgáljuk a g-t az a-ban. g'(a) < 0, ezért
Ekkor természtesen egy valamely ε>0-ra minden x ∈ (a,a+ε)-re
és innen
vagyis a-ban nem lehet g-nek minimuma. De ugyanilyen érveléssel g'(b) > 0 miatt valamely ε>0 számmal ha x ∈ (b-ε,b), akkor x-b < 0 és
azaz b-ben sem lehet minimum. Viszont ez azt jelenti, hogy a Weierstrass-tétel által garantált minimum csak az (a,b) nyíltban lehet. QED
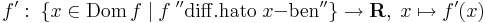
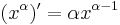

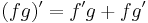
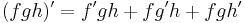
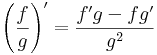
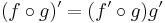
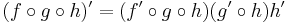
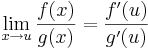
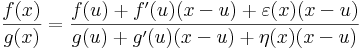
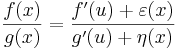
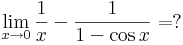
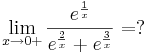
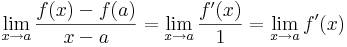
![g(x):=f(x)-mx,\quad\quad x\in[a,b]](/upload/math/6/a/a/6aa43cd2fc4c4d458b4c65f5ec657da4.png)