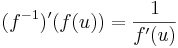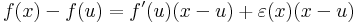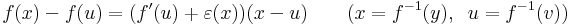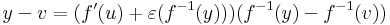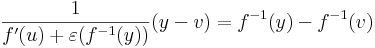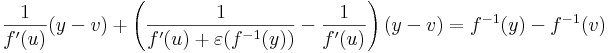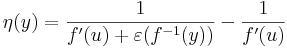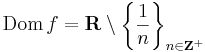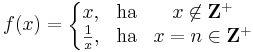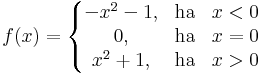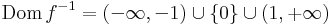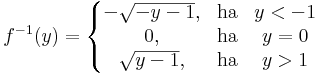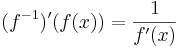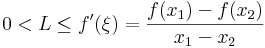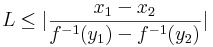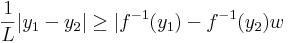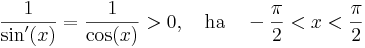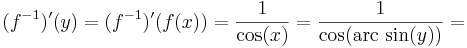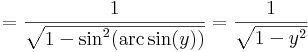Szerkesztő:Mozo/A2 szigorlat 9
Mozo (vitalap | szerkesztései) (Új oldal, tartalma: „==Inverzfüggvénytétel '''R'''-re== '''Inverzfüggvény deriváltja.''' Ha az ''f'' invertálható függvény differenciálható ''u''-ban, ''f'' <sup>-1</sup> folyt…”) |
Mozo (vitalap | szerkesztései) (→Inverzfüggvénytétel R-re) |
||
| 14. sor: | 14. sor: | ||
függvény akkor lesz folytonos és ''v''-ben eltűnő, ha maga f<sup>-1</sup> is folytonos ''v''-ben. | függvény akkor lesz folytonos és ''v''-ben eltűnő, ha maga f<sup>-1</sup> is folytonos ''v''-ben. | ||
| − | ''' | + | '''Megjegyzés.''' A tételi állításban az inverz folytonossági feltétele csak olyan esetben jelent megszorítást, amikor a függvény nem intervallumon értelmezett szigorúan monoton függvény. Példa olyan invertálható függvényre, melynek deriváltja nem nulla egy adott pontban, de inverze a képpontban nem folytonos: |
:<math>\mathrm{Dom}\,f=\mathbf{R}\setminus\left\{\frac{1}{n}\right\}_{n\in \mathbf{Z}^+}</math> | :<math>\mathrm{Dom}\,f=\mathbf{R}\setminus\left\{\frac{1}{n}\right\}_{n\in \mathbf{Z}^+}</math> | ||
:<math>f(x)=\left\{\begin{matrix}x, & \mathrm{ha} & x\not\in \mathbf{Z}^+\\ | :<math>f(x)=\left\{\begin{matrix}x, & \mathrm{ha} & x\not\in \mathbf{Z}^+\\ | ||
| 32. sor: | 32. sor: | ||
x^2+1, & \mathrm{ha} & x>0 | x^2+1, & \mathrm{ha} & x>0 | ||
\end{matrix}\right.</math> | \end{matrix}\right.</math> | ||
| − | ''Megoldás.'' Persze, hisz a negatívokon invertálható és csak negatív értéket vesz fel. A pozitívokon szintén és szintén csak pozitív értékeket vesz fel. A 0-beli érték az előző | + | ''Megoldás.'' Persze, hisz a negatívokon invertálható és csak negatív értéket vesz fel. A pozitívokon szintén és szintén csak pozitív értékeket vesz fel. A 0-beli érték az előző képhalmazokon kívül esik (a 0). Az inverz: |
:<math>\mathrm{Dom}\,f^{-1}=(-\infty,-1)\cup\{0\}\cup(1,+\infty)</math> | :<math>\mathrm{Dom}\,f^{-1}=(-\infty,-1)\cup\{0\}\cup(1,+\infty)</math> | ||
:<math>f^{-1}(y)=\left\{\begin{matrix} | :<math>f^{-1}(y)=\left\{\begin{matrix} | ||
| 52. sor: | 52. sor: | ||
''Bizonyítás.'' 1) A derivált mindenhol azonos előjelű, ellenkező esetben lenne két hely, ahol különböző, de a Darboux-tétel miatt akkor lenne zérushelye is a deriváltnak, ami ellentmond a feltételeknek. Tehát ''f'' szigorúan monoton, így invertálható. | ''Bizonyítás.'' 1) A derivált mindenhol azonos előjelű, ellenkező esetben lenne két hely, ahol különböző, de a Darboux-tétel miatt akkor lenne zérushelye is a deriváltnak, ami ellentmond a feltételeknek. Tehát ''f'' szigorúan monoton, így invertálható. | ||
| − | 2) Minden ''a'' ∈ I pontban a derivált nem nulla és folytonos, így létezik olyan | + | 2) Minden ''a'' ∈ I pontban a derivált nem nulla és folytonos, így létezik olyan környezete, melyben a derivált mindenhol egy L pozitív számál nagyobb. Ezért a Lagrange-tétel miatt a környzet bármely két <math>x_1</math>, <math>x_2</math> pontjára: |
:<math>0<L\leq f'(\xi)=\frac{f(x_1)-f(x_2)}{x_1-x_2}</math> | :<math>0<L\leq f'(\xi)=\frac{f(x_1)-f(x_2)}{x_1-x_2}</math> | ||
Emiatt az x=f<sup>-1</sup>(y) áttéréssel: | Emiatt az x=f<sup>-1</sup>(y) áttéréssel: | ||
| 58. sor: | 58. sor: | ||
azaz | azaz | ||
:<math>\frac{1}{L}|y_1-y_2|\geq |f^{-1}(y_1)-f^{-1}(y_2)w\,</math> | :<math>\frac{1}{L}|y_1-y_2|\geq |f^{-1}(y_1)-f^{-1}(y_2)w\,</math> | ||
| − | azaz az inverz lipschitzes a | + | azaz az inverz lipschitzes a környezetben, azaz a pontban folytonos. |
3) 4) ezt egyszerre igazoljuk. Az ''u''-beli diffhatóság miatt: | 3) 4) ezt egyszerre igazoljuk. Az ''u''-beli diffhatóság miatt: | ||
:<math>f(x)-f(u)=f'(u)(x-u)+\varepsilon(x)(x-u)\,</math> | :<math>f(x)-f(u)=f'(u)(x-u)+\varepsilon(x)(x-u)\,</math> | ||
| 88. sor: | 88. sor: | ||
Ekkor a globális inverzfüggvény-tételből következőleg a g szigorúan monoton, inverze differenciálható és kifejezhető x=g(t)-ből a t: | Ekkor a globális inverzfüggvény-tételből következőleg a g szigorúan monoton, inverze differenciálható és kifejezhető x=g(t)-ből a t: | ||
:<math>t=g^{-1}(x),\quad x\in [c,d]</math> | :<math>t=g^{-1}(x),\quad x\in [c,d]</math> | ||
| − | ahol [c,d] a g | + | ahol [c,d] a g értékkészlete. |
Ezzel a görbe implicit módon is megadható lesz, mint az | Ezzel a görbe implicit módon is megadható lesz, mint az | ||
| 98. sor: | 98. sor: | ||
amit Cauchy-féle középértékételnek nevezünk. | amit Cauchy-féle középértékételnek nevezünk. | ||
| − | Ebből következtethetünk az erős L'Hospital-szabály első | + | Ebből következtethetünk az erős L'Hospital-szabály első deriváltas alakjára:--> |
A lap 2017. május 21., 10:23-kori változata
Inverzfüggvénytétel R-re
Inverzfüggvény deriváltja. Ha az f invertálható függvény differenciálható u-ban, f -1 folytonos u-ban és f'(u) ≠ 0, akkor az inverz is differenciálható u-ban és
Biz.
Itt az
függvény akkor lesz folytonos és v-ben eltűnő, ha maga f-1 is folytonos v-ben.
Megjegyzés. A tételi állításban az inverz folytonossági feltétele csak olyan esetben jelent megszorítást, amikor a függvény nem intervallumon értelmezett szigorúan monoton függvény. Példa olyan invertálható függvényre, melynek deriváltja nem nulla egy adott pontban, de inverze a képpontban nem folytonos:
f ekkor a 0-ban deriválható és f '(0)=1, invertálható, mert R \ (1/Z+) \ Z+-n az identitás és az Z+-n pedig az 1/id, mely értékei vétetnek fel az R \ (1/Z+)- halmaz képeiként. Viszont így f-1 nem korlátos 0-ban, azaz nem folytonos, így nem is differenciálható.
Állítás. Intervallumon értelmezett szigorúan monoton függvény inverze folytonos (tehát ez esetben még akkor is folytonos az inverz, ha a függvénynek magának ugrása van).
Erre a meglepő eredményre egy illusztráló példát adunk.
Példa. Folytonosan invertálható-e az alábbi függvény? Indokoljuk a fenti tétel nélkül!
Megoldás. Persze, hisz a negatívokon invertálható és csak negatív értéket vesz fel. A pozitívokon szintén és szintén csak pozitív értékeket vesz fel. A 0-beli érték az előző képhalmazokon kívül esik (a 0). Az inverz:
Ez a függvény mindenütt folytonos, mert a gyök az, és a 0-ban izolált pontja van, ahol a függvények triviálisan folytonosak.
Tétel -- Globális inverzfüggvény-tétel -- Ha f: I  R függvény folytonosan differenciálható és f' sehol se nulla, akkor
R függvény folytonosan differenciálható és f' sehol se nulla, akkor
- f invertálható
- f inverze folytonos (f homeomorfizmus)
- f inverze deriválható (f diffeomorfizmus)
- minden x ∈ I-re
Megjegyzés. Részletesebb indoklás azt is kimutatja, hogy a derivált folytonossága nem szükséges (bár nem árt :).
Bizonyítás. 1) A derivált mindenhol azonos előjelű, ellenkező esetben lenne két hely, ahol különböző, de a Darboux-tétel miatt akkor lenne zérushelye is a deriváltnak, ami ellentmond a feltételeknek. Tehát f szigorúan monoton, így invertálható.
2) Minden a ∈ I pontban a derivált nem nulla és folytonos, így létezik olyan környezete, melyben a derivált mindenhol egy L pozitív számál nagyobb. Ezért a Lagrange-tétel miatt a környzet bármely két x1, x2 pontjára:
Emiatt az x=f-1(y) áttéréssel:
azaz
azaz az inverz lipschitzes a környezetben, azaz a pontban folytonos. 3) 4) ezt egyszerre igazoljuk. Az u-beli diffhatóság miatt:
Itt az
függvény akkor lesz folytonos és v-ben eltűnő, ha maga f-1 is folytonos v-ben.
Példa. Igazoljuk, hogy létezik a sin inverze a [-π/2,π/2]-n és az inverz folytonos a [-1,1]-en (ez az arcsin) ezen kívül az inverz deriválható a belső pontokban!
Ugyanis. [-π/2,π/2]-n a sin szigorúan monoton nő és inverz képe [-1,1]. Emiatt ez folytonos is és az inverzfüggvény-tétel miatt a nyílton differenciálható, ugyanis
az inverze: