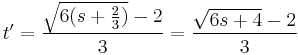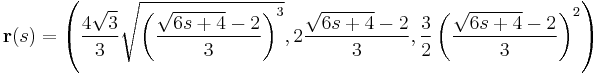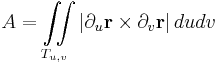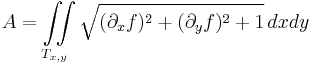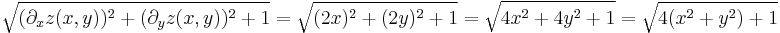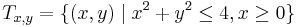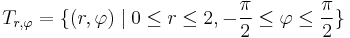Szerkesztő:Mozo/A3 gyakorló feladatok 6.
Differenciálgeometria
Ívhossz és ívhosszparaméterezés
1. a) Mi az alábbi görbe ívhossza a [1,e] paraméterszakaszon és mi az ívhosszparaméterezése t=1-tól kezdődően?
b) Mi az alábbi görbe ívhossza a [0,1] paraméterszakaszon és mi az ívhosszparaméterezése t=0-tól kezdődően?
MO.: a)
Ívhossz: [1,e]-n:
Ívhossz paraméterezés t=1-től:
b)
Vegyük észre, hogy a négyzetgyök alatt teljes négyzet áll:
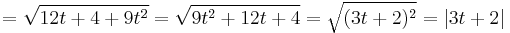 ez t>0-ra persze azonos 3t+2-vel.
ez t>0-ra persze azonos 3t+2-vel.
Ívhossz: [1,e]-n:
Ívhossz paraméterezés t=0-tól:
Felszín
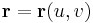 esetén
esetén
z = f(x,y) esetén
2. a) Számítsuk ki a z = x2 − y2 egyenlettel adott felület azon darabjának felszínét, melyet az 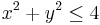 ,
, 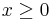 feltételek adnak meg!
feltételek adnak meg!
b) Számítsuk ki a 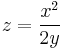 egyenlettel adott felület azon darabjának felszínét, melyet az
egyenlettel adott felület azon darabjának felszínét, melyet az 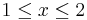 ,
, 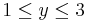 feltételek adnak meg!
feltételek adnak meg!
c) Számítsuk ki az 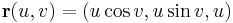 felület azon darabjának felszínét, melyet a
felület azon darabjának felszínét, melyet a 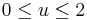 ,
, 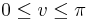 feltételek adnak meg!
feltételek adnak meg!
MO.: a)
Mivel a tartomány is és a függvény is hengerszimmetriát mutat (minden amiben x2 + y2 van, az hengerszimmetrikus), ezért az integrált hengerkoordinátákban számítjuk ki. A tartomány derékszögű és polárparamméterezése (érdemes felrajzolni koordniátarendszerben és leolvasni az r-t, φ-t):
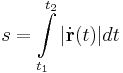
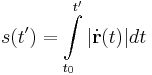
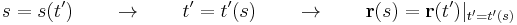
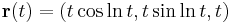
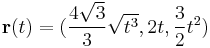
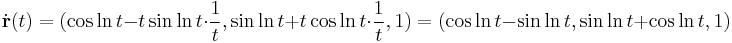
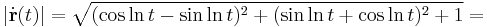
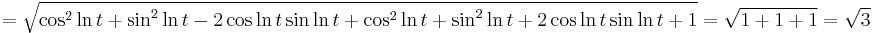
![s=\int\limits_{1}^{e}\sqrt{3}\,dt=[\sqrt{3}\cdot t]_1^e=\sqrt{3}(e-1)](/upload/math/8/a/e/8ae6fa50ae7913b97d548d4c42555382.png)
![s(t')=\int\limits_{t=1}^{t'}\sqrt{3}\,dt=[\sqrt{3}\cdot t]_{1}^{t'}=\sqrt{3}(t'-1)\qquad\to\qquad t'=\frac{s}{\sqrt{3}}+1](/upload/math/6/6/c/66c8f8e4158ede597163e21e7b3cbd50.png)
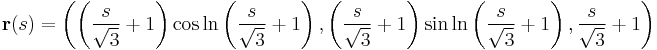
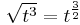
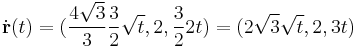
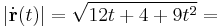
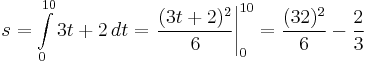
![s(t')=\int\limits_{t=1}^{t'}3t+2\,dt=\left[\frac{(3t+2)^2}{6}\right]_{0}^{t'}=\frac{(3t'+2)^2}{6}-\frac{2}{3}](/upload/math/1/2/e/12edcafdbb5d1a8fc9bb04163fccaf88.png)