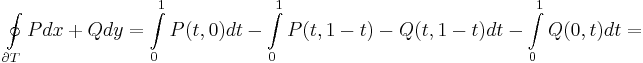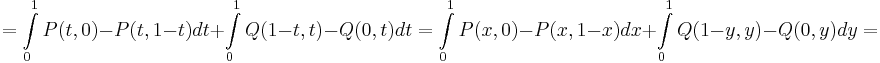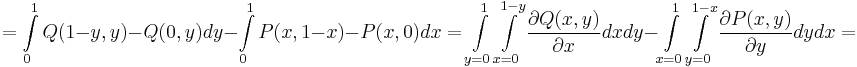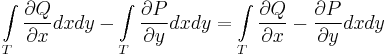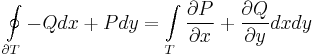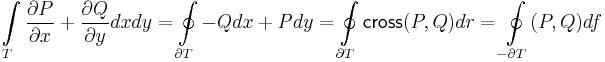Szerkesztő:Mozo/ A3 bizonyítások
Mozo (vitalap | szerkesztései) (→Komplex differenciálhatóság) |
Mozo (vitalap | szerkesztései) (→Potenciál) |
||
| 357. sor: | 357. sor: | ||
vonalintegrál. | vonalintegrál. | ||
| + | ===Jellemzés=== | ||
A potenciálosság rendkívül szoros kapcsolatban van a cirkulációval és a rotációval: | A potenciálosság rendkívül szoros kapcsolatban van a cirkulációval és a rotációval: | ||
| 390. sor: | 391. sor: | ||
skalárfüggvény független az úttól és a felső határ szerinti gradiense ugyanúgy az integrandus, mint az egyváltozós valós függvények esetén. QED. | skalárfüggvény független az úttól és a felső határ szerinti gradiense ugyanúgy az integrandus, mint az egyváltozós valós függvények esetén. QED. | ||
| − | Az előbb említett, az integrálfüggvény deriválhatóságának tételének megvan a párja is. Ez az ''első | + | ===Gradiensre vonatkozó integráltétel=== |
| + | |||
| + | Az előbb említett, az integrálfüggvény deriválhatóságának tételének megvan a párja is. Ez az ''első gradienstétel'', mely végül is nem más, mint a Newton--Leibniz-formula többdimenziós általánosításai közül a legelső verzió: | ||
'''Tétel.''' | '''Tétel.''' | ||
| 402. sor: | 405. sor: | ||
2) integrálás és az I. grad. tétel alkalmazása | 2) integrálás és az I. grad. tétel alkalmazása | ||
3) invariáns alakban adott feldatoknál primitívfüggvény keresés. | 3) invariáns alakban adott feldatoknál primitívfüggvény keresés. | ||
| − | Ez utóbbi | + | |
| + | ===Hossz n-edik deriváltja=== | ||
| + | Ez utóbbi megoldáshoz tudnunk kell, hogy a hossz n-edik deriváltja mi. Ezt a többváltozós függvények analízisében az összetett függvény deriválásánál tanultuk: | ||
ha '''r''' nem nulla, akkor | ha '''r''' nem nulla, akkor | ||
:<math>\mathrm{grad} |\mathbf{r}|^n =n|\mathbf{r}|^{n-1}\frac{\mathbf{r}}{|\mathbf{r}|} | :<math>\mathrm{grad} |\mathbf{r}|^n =n|\mathbf{r}|^{n-1}\frac{\mathbf{r}}{|\mathbf{r}|} | ||
A lap 2014. január 1., 23:28-kori változata
Tartalomjegyzék |
Egzakt differenciálegyenlet
Definíció
Legyen U ⊆ R2 nyílt halmaz és P,Q: U  R folytonos függvények, Q sehol sem nulla. Azt mondjuk, hogy az
R folytonos függvények, Q sehol sem nulla. Azt mondjuk, hogy az
differenciálegyenlet egzakt, ha létezik olyan F: U  R folytonosan differenciálható függvény, hogy
R folytonosan differenciálható függvény, hogy
Elméleti példa. Minden
alakú szeparábilis differenciálegyenlet egzakt, hiszen ha g integrálfüggvénye G, akkor
Alkalmas tehát az alábbi függvény:
Jelen esetben a G függvény deriváltja (G'=g) sehol sem nulla folytonos függvény, ezért szigorúan monoton. Emiatt kifejezhető y éspedig:
Megjegyzés. A megoldásokat implicit módon adja meg az
egyenlet. Mivel
ezért az implicitfüggvény-tétel miatt y-t "ki lehet fejezni". Érdemes felelevenítenünk magát az implicitfüggvény-tételt:
Implicitfüggvény-tétel -- Ha a Φ: I×J  R folytonosan differenciálható függvény az (x0,y0) ∈ int(I×J) pontban teljesíti a ∂Φ/∂y ≠ 0 feltételt, akkor a (x0,y0) pont egy környezetében egyértelműen létezik az Φ(x,y)=Φ(x0,y0) egyenletnek az (x0,y0) ponton áthaladó implicit függvénye, azaz az x0 egy K⊆I környezetében értelmezett, J-beli értékű y deriválható függvény, melyre minden x ∈ K esetén:
R folytonosan differenciálható függvény az (x0,y0) ∈ int(I×J) pontban teljesíti a ∂Φ/∂y ≠ 0 feltételt, akkor a (x0,y0) pont egy környezetében egyértelműen létezik az Φ(x,y)=Φ(x0,y0) egyenletnek az (x0,y0) ponton áthaladó implicit függvénye, azaz az x0 egy K⊆I környezetében értelmezett, J-beli értékű y deriválható függvény, melyre minden x ∈ K esetén:
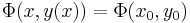 ,
, 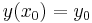
és ennek deriváltja minden x ∈ K-ban:
Egzakt egyenlet egzisztencia- és unicitástétele
Tétel. Legyenek P és Q az U ⊆ R2 nyílt halmazon értelmezett folytonos valós függvények, Q sehol se nulla, grad F = (P,Q) valamely F: U  R folytonosan differenciálható függvénnyel és (x0,y0) ∈ U. Ekkor
R folytonosan differenciálható függvénnyel és (x0,y0) ∈ U. Ekkor
1) az
- (ex) y'=-P/Q
egyenletnek egyértelműen létezik az y0 = y(x0) kezdeti feltételt kielégítő y lokális megoldása és
2) az
- (impl) F(x,y) = F(x0,y0)
egyenlet (x0,y0)-on áthaladó egyetlen lokális implicit függvénye az (ex) egyenlet y(x0) = y0 kezdeti feltételt kielégítő egyetlen lokális megoldása.
Biz. 1) Egzisztencia. Belátjuk, hogy (impl) egyetlen (x0,y0)-on áthaladó implicit függvénye megoldása az (ex) egyenletnek.
így az implicitfüggvény-tétel szerint, egyértelműen létezik F-nek y=y(x) implicit függvénye az adott pont egy környezetében és ennek deriváltja az értelmezési tartományának minden pontjában:
tehát y az (ex) differenciálegyenletnek is megoldása, és ez kielégíti a kezdeti feltételt.
Unicitás. Tegyük fel, hogy létezik megoldása a kezdeti érték feladatnak. Legyen egy tetszőleges megoldása y, azaz
Ez az egyenlet a grad F = (P,Q) miatt előáll
alakban. Most belátjuk, hogy y (impl)-nek implicit megoldása. Az összetett függvény differenciálási szabálya miatt ( d(F G)(x,y)=dF(G(x,y))
G)(x,y)=dF(G(x,y)) dG(x,y) ) az előző egyenlet a következő formában is írható:
dG(x,y) ) az előző egyenlet a következő formában is írható:
x értékei egy intervallumból kerülnek ki, ezért az integrálszámítás alaptétele szerint az x  F(x,y(x)) egy konstans függvény. De a feltétel szerint y(x0) = y0 teljesül, ezért x
F(x,y(x)) egy konstans függvény. De a feltétel szerint y(x0) = y0 teljesül, ezért x  y(x) egy (x0,y0)-on áthaladó implicit függvénye az F(x,y)=F(x0,y0) egyenletnek. Ez az utóbbi azonban egyértelműen van meghatározva, ezért a kezdeti érték feladat minden megoldása egybeesik ezzel az implicit függvénnyel, azaz a megoldás egyértelmű.
y(x) egy (x0,y0)-on áthaladó implicit függvénye az F(x,y)=F(x0,y0) egyenletnek. Ez az utóbbi azonban egyértelműen van meghatározva, ezért a kezdeti érték feladat minden megoldása egybeesik ezzel az implicit függvénnyel, azaz a megoldás egyértelmű.
2) Az implicitfüggvény tételében adott egyetlen implicit függvény az 1) egzisztencia része miatt megoldása (ex)-nek és 1) unicitás része miatt ez az egyetlen megoldása (ex)-nek.
Az egzaktság jellemzése
Megjegyzés. Az egzakt differenciálegyenletet még
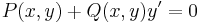 ill.
ill. 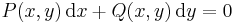
alakban is szokás írni.
Ez utóbbi egyenletről azt is mondják, hogy akkor egzakt, ha a P(x,y)dx + Q(x,y)dy kifejezés "teljes differenciál", amin azt értik, hogy létezik olyan F(x,y) függvény, melynek teljes differenciálja:
Ezt a mai jelölésekkel a következőképpen írjuk. Egy F kétváltozós függvény teljes differenciálja egy lineáris leképezés, mely a sztenderd {(1,0),(0,1)} bázisban felírt koordinátáival nem más, mit a parciális deriváltjainak sormátrixa:
Emiatt a (C) feltétel a következő alakban is írható:
![[\mathrm{d}F]=\left[P,Q\right]\,](/upload/math/3/4/3/343e00846494e553e629c9e57344a211.png) ill.
ill. ![\mathrm{grad}\,F=[P,Q]\,](/upload/math/4/f/9/4f9b9ba5601098c77e15e1f242d50948.png)
Tehát az egzakt egyenletben a (P,Q) vektormező (vektorértékű függvény) potenciálos. Innen hasznos jellemzést kapunk az egzaktságra a vektoranalízisbeli ismereteinkből.
Tétel. Legyen U egyszeresen összefüggő nyílt halmaz, P,Q: U  R folytonosan differenciálható függvények (Q sehol sem nulla). A Pdx + Qdy = 0 egyenlet pontosan akkor egzakt, ha
R folytonosan differenciálható függvények (Q sehol sem nulla). A Pdx + Qdy = 0 egyenlet pontosan akkor egzakt, ha
Az F függvényt, az Pdx + Qdy = 0 egyenlet integráljának nevezzük.
Ezt a tételt jól ismerjük és a bizonyítását a vektoranalízisben vettük.
Megjegyzés. 1) A feltétel nem más, mint az, hogy a (P,Q) síkbeli vektormező rotációja azonosan nulla. Ugyanis a rotáció a síkbeli (P,Q) vektormező esetén:
2) Bár a szeparábilis egyenlet egzakt, a fenti feltétel az egzaktság ellenőrzésére sokkal szigorúbb mint a szeparábilis egyenlet megoldhatóságának feltétele.
Lineáris differenciálegyenletek
Inhomogén lineáris egyenlet megoldásai
Tétel. Ha V, W tetszőleges lineáris tér, A ∈ Lin(V,W) lineáris operátor, b ∈ W. Ha x0 ∈ V megoldása az Ax = b inhomogén egyenletnek, akkor az
összes megoldásainak halmaza:
Bizonyítás. 1) Ha x ∈ Ker(A), akkor Ax = 0. Ekkor
azaz ekkor x+x0 ∈ M.
2) Ha
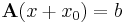 és
és 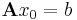
akkor
tehát x ∈ Ker(A). QED.
Megjegyzés. Tudjuk tehát akármilyen lineáris térben az inhomogén egyenlet összes megoldását, ha ismert egy megoldása. Ha tehát Ax=b lineáris differenciálegyenlet, akkor a tétel azt a szlogent fejezi ki, hogy inhomogén lineáris differenciálegyenlet általános megoldása egyenlő a homogén egyenlet általános megoldása plusz az inhomogén egyenlet egy partikuláris megoldása.
Elsőrendű inh. lin. diff. egyenlet és az állandó variálása
Állítás. Ha f: I  R folytonos függvény akkor az
R folytonos függvény akkor az
lineáris operátor a Lin(C1(I),C(I)) téren.
Bizonyítás.
Következmény. A fenti jelölésekkel, tetszőleges g folytonos függvényre, ha y0 a
differenciálegyenlet egy megoldása, akkor az egyenlet általános megoldása egyenlő a
homogén egyenlet általános megoldása plusz y0.
Példa. Oldjuk meg az
egyenletet! A partikuláris megoldást keressük az állandók variálása módszerével!
Másodrendű, áll. ehós hom. egyenlet
Tétel. Ha a,b ∈ R, akkor az
C2(I)  C(I) lineáris operátor magja kétdimenziós.
C(I) lineáris operátor magja kétdimenziós.
Megoldás. A bizonyítás két részből fog állni. Először is Laplace-transzformációval belátjuk, hogy ha dim Ker(A) legalább kettő, akkor legfeljebb 2. Másodszor pedig mutatunk 2 lineárisan független megoldást.
Bizonyítás nélkül elfogadjuk azt a tényt, hogy ha ezen egyenlet esetén egy adott pontban kezdeti értéket adunk az y-nak és az y'-nek akkor a megoldás (ha van) egyértelmű. Szemléletes képpel, ez azt jelenti, hogy ha a kezdőfázist és a sebességet megadjuk, akkor azzal a teljes hullámformát megkapjuk.
I. Legyen y1 és y2 két lineárisan független megolása az
- A y = 0
egyenletnek és legyen y ∈ Ker(A) tetszőleges. Rögzítsünk egy x0 ∈ I helyet, melyen y(x0) = u és y'(x0) = v. Elő fogjuk állítani ezt a partikuláris megoldást a két előbbi megoldás lineáris kombinációjaként. Legyenek:
azt kívánjuk elérni, hogy az
- αu1 + βu2 = u
- αv1 + βv2 = v
egyenletrendszernek legyen egyértelmű megoldása (α,β)-ra. Ez pontosan akkor van, ha a
determináns (azaz az egyenletrendszer x0-beli Wronsky-determinánsa) nem nulla. Hiszen ekkor a megoldás egyértelműsége miatt (azaz, hogy u és v egyértelműen meghatározza y-t) azt kapjuk, hogy (α,β) "globális konstansok is", azaz αy1 + βy2 = y.
Az egyenlet Laplace-transzformáltja:
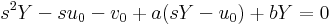
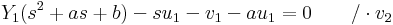
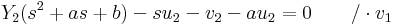
- (s2 + as + b)(v2Y1 − v1Y2) + (s + a)(u2v1 − u1v2) = 0
Ennek az egyenletnek minden s-re fenn kell állnia, ezért ha u2v1 − u1v2 = 0 lenne, akkor v2Y1 − v1Y2 = 0 is lenne (minden s-re), azaz Y2 és Y1 lineárisan kifejezhetők lennének egymással, ami ellentmondana a rájuk tett kezdeti feltevésnek.
II. A megoldéskeresési feladatot kicsit bővebb körben, a valós változós, komplex értékű kétszer folytonosan R-differenciálható függvények körében oldjuk meg. Tehát ekkor A a C2(I,C) térből a C(I,C) térbe hat. Ezek között fogunk valós megoldás keresni. A differenciáloperátornak sajátfüggvénye az exponenciális függvény, így tetszőleges λ ∈ C
próbafüggvény behelyettesítésével kapjuk:
Tehát a megoldások:
1. ha λ1 ≠ λ2 valósak, akkor
bázis, mert lineárisan függetlenek és éppen ezért I. miatt előállítják Ker(A)-t:
2. ha λ1 = λ2 valósak, akkor keresnünk kell mégegy az eλx-től lineárisan független megoldást.
Világos, hogy ez az, hiszen a 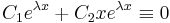 egyenletet eλx-vel leosztva, a polinom balodalú
egyenletet eλx-vel leosztva, a polinom balodalú 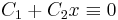 adódna, ami csak akkor lehet a nullapolinom, ha az ehók mind nullák.
adódna, ami csak akkor lehet a nullapolinom, ha az ehók mind nullák.
3. ha λ = α 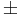 βi nemvalós, akkor
βi nemvalós, akkor
azaz
megoldások, melyek azonban komplexek. De ezeket összeadva, illetve a különbségüket i-vel beszorozva már valós megoldásokat kapunk (ezek az előbbi végzett műveletek lineárisak voltak, így a függvények megoldás mivoltán nem változtattak). Azaz:
a tér pedig:
bázis, mert lineárisan függetlenek és éppen ezért I. miatt előállítják Ker(A)-t.
Komplex differenciálhatóság
Definíció - Komplex differenciálhatóság, komplex derivált - Legyen f a z0 egy környezetében értelmezett függvény. Azt mondjuk, hogy f C-deriválható z0-ban és deriváltja a w szám, ha
Jelölése: f'(z0).
Azt, hogy az f a z0-ban komplex deriválható még úgy is jelöljük, hogy
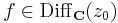 .
.
Megj. Hasonlóképpen a valós egyváltozós esethez az f komplex differenciálhatósága z0-ban ekvivalens azzal, hogy létezik olyan ε(z) függvény, mely a z0-ban a 0-hoz tart, ott folytonos és minden z-re az értelmezési tartományból:
Példa. A következő függvény komplex deriválható a 0-ban:
Mo. A különbségi hányados:
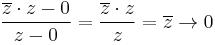 , ha z tart nullába.
, ha z tart nullába.
Példa. Az alábbi függvény nem deriválható komplex módon a 0-ban:
Mo. A különbségi hányados:
Ennek a határértéke nem létezik a nullában.
Jellemzés
Tétel. - A komplex differenciálhatóság jellemzése - Legyen f a z0 = x0 + iy0 egy környezetében értelmezett függvény. Ekkor az alábbiak ekvivalensek:
- 1)
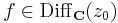
- 2)
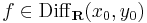 és
és ![[\mathrm{d}f(x_0,y_0)]\in\mathbf{C}](/upload/math/b/9/7/b975f630a8a50e0bde8a08b28b2c681d.png) .
.
Bizonyítás. Legyen f a z0 = x0 + iy0 egy környezetében értelmezett függvény és w komplex szám. Tekintsük a következő határértéket:
ahol az z, z0, f(z), f(z0) mennyisegekre ugy tekintunk, mint vektorokra. Ez ekvivalens a következővel:
ahol az elobb emlitettek mar algebrai ertelemben komplex szamok, nem feltetlenul vektorok. Azaz
Itt (z-z0)/|z-z0| a komplex egységkörön "futó" függvény, hossza 1, ezért a fenti ekvivalnes a következővel:
Ami viszont ugyanakkor igaz mint:
Ha a következtetésben felfelé vizsgálódunk, tehát feltesszük a komplex deriválhatóságot ahol w a komplex derivált, akkor azt kapjuk, hogy a w mátrixreprezentációjával való mátrixszorzás alkalmas lineáris leképezés a valós derivált számára, azaz létezik [df(z0)]=[w].
Másfelől, ha f valósan deriválható és a deriváltja a w komplex számot reprezentálja, akkor komplexen is deriválható es komplex derivaltja pont w.
Cauchy--Riemann-egyenletek A fenti tételben a [df(z)] ∈ C feltétel (természetesen a totális deriválhatóság esetén) ekvivalens az alábbiakkal. Ha f = u + iv és z = x +iy, akkor
Komplex deriváltfüggvény Ahol egy f komplex függvény komplex deriválható, ott a deriváltja:
Definíció - Regularitás - Az f komplex függvény reguláris a z pontban, ha f a z egy egész környezetén értelmezett, és a teljes környezetben komplex deriválható.
Egy tétel a reziduumról
Tétel. Ha f-nek k-adrendű pólusa van a 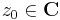 -ben (k>0), akkor
-ben (k>0), akkor
Az, hogy f-nek k-adrendű pólusa van a z0-ban, az azt jelenti, hogy ott izolált szingularitása van, és a Laurent-sorában a legmagasabb 1/(z-z0) hatvány kitevője k. Legyen
Tudjuk, hogy
ezért  már egy Taylor-sor, reguláris és világos, hogy a c-1 tagot a Taylor-sora k-1-edik tagjának együtthatójából számíthatjuk ki:
már egy Taylor-sor, reguláris és világos, hogy a c-1 tagot a Taylor-sora k-1-edik tagjának együtthatójából számíthatjuk ki:
de a hatványsor tagjainak egyértelműségéből következik, hogy
ezért
Potenciál
A továbbiakban feltesszük, hogy a v vektorfüggvény folytonosan differenciálható.
Azt mondjuk, hogy a v vektorfüggvény potenciálos, ha van olyan u skalárfüggvény, mely differenciálható és
A v vektorfüggvény cirkulációja a Γ egyszerű zárt görbén a
vonalintegrál.
Jellemzés
A potenciálosság rendkívül szoros kapcsolatban van a cirkulációval és a rotációval:
Tétel. Ha v folyt. diff. vektormező az A egyszeresen összefüggő tartományon. Ekkor az alábbi három kijelentés egymással egyenértékű (v folyt. diff. vektormező):
- v potenciálos,
- v rotációja minden pontban nulla,
- v cirkulációja minden zárt görbére nulla (más kifejezéssel: v konzetvatív).
Bizonyítás.
1. --> 2. Tegyük fel, hogy grad u = v, így rot v = rot grad u. Ekkor formálisan hivatkozhatunk például a vektoriális szorzás azon szabályára, hogy párhuzamos vektorok vektoriális szorzata 0, hisz
De itt végül is a Young-tételről van szó. Komponensenként kiírva:
kétszer folytonsan differenciálható u Hesse-mátrixa szimmertikus, azaz a vegyes másodrendű parciális deriváltak egyenlők, azaz a fenti összeg 0.
2. --> 3. Itt a Stokes-tételre kell hivatkoznunk:
egyszeresen összefüggő tartományban haladó Γ = ∂F görbére és tetszőleges olyan F felületre, melynek ő a pereme. De rot v mindenhol 0. így a jobb oldal 0, azaz cirkuláció is.
3. --> 1. Belátjuk, hogy van potenciál. Legyen a rögzített pont és b tetszőlegesen választott. Legyen Γ1 és Γ2 két tetszőleges görbe, mely a-ból b-be megy. Ekkor az egyszeres összefüggőség miatt a Γ2 -t visszfelé irányítva:
az a zárt görbe, mely az a-ból megy a Γ1 mentén a b-be és a b-ből megy a Γ2 mentén, de ellenkezőleg irányítva az a-ba. De v minden körintegrálj eltűnik, így
azaz
Tehát az
skalárfüggvény független az úttól és a felső határ szerinti gradiense ugyanúgy az integrandus, mint az egyváltozós valós függvények esetén. QED.
Gradiensre vonatkozó integráltétel
Az előbb említett, az integrálfüggvény deriválhatóságának tételének megvan a párja is. Ez az első gradienstétel, mely végül is nem más, mint a Newton--Leibniz-formula többdimenziós általánosításai közül a legelső verzió:
Tétel.
(ha u folyt. diff. és egysz. öf. tartományon ért.)
A tétel beleillik a "nagy integrálátalakító tételek" sorába (Stokes-tétel, Gauss--Osztrogradszkij-tétel és most az I. gradienstétel), melyek alapszlogenje, hogy "integrál a peremen = a derivált integrálja belül", persze itt a perem az {a,b} véges halmaz, a derivált a gradiens, a "belül" pedig a Γ görbe. (S.-t-nél felület a belső, a határán futó zárt görbe a perem és rot a derivált, G--O-t nél térrész a belső, az őt határoló zárt felület a perem és div a derivált).
Potenciálkeresés. 1) Pancsolásos módszer és variánsai (alkalmazások: egzakt differenciálegyenlet megoldása, harmonikus társ keresése) 2) integrálás és az I. grad. tétel alkalmazása 3) invariáns alakban adott feldatoknál primitívfüggvény keresés.
Hossz n-edik deriváltja
Ez utóbbi megoldáshoz tudnunk kell, hogy a hossz n-edik deriváltja mi. Ezt a többváltozós függvények analízisében az összetett függvény deriválásánál tanultuk: ha r nem nulla, akkor
mert a külső függvény: 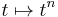 , a belső pedig
, a belső pedig 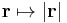 . Az utóbbi deriváltja koordinátás alakban:
. Az utóbbi deriváltja koordinátás alakban:
tehát a függvénykompozíció deriválására vonatkozó tétel szerint:
Komplex körintegrálok
Ebben a tételben a komplex körintegrálok kiszámításával foglalkozunk.
Definíció. Ha G:[a,b] C görbe és f olyan komplex függvény, melyre Ran(G)⊆Dom(f), és f folytonos, akkor belátható, hogy létezik a
C görbe és f olyan komplex függvény, melyre Ran(G)⊆Dom(f), és f folytonos, akkor belátható, hogy létezik a
határérték, mely egy speciális Riemann-közelítőösszeg határértéke. Itt a görbén kijelöltük a véges sok zi pontot, melyek a szigorúan monoton (ti)-khez tartoznak a zi = z(ti) definícióval. Ezen [z(ti),z(ti + 1)] görbeszakaszokon belül felvettük tetszőlegesen a ζi közbülső pontokat, és a Δzi=[z(ti),z(ti + 1)] szakaszokkal elkészítettük az f(ζi)Δzi komplex szorzatokat. A határérték ezek görbére vett összegének határértéke. Ez a határérték az f függvény G-re vett komplex integrálja.
Kiszámítási formula. Belátható, hogy a fenti integrál a következőkkel egyenlő:
Megjegyzes A helyettesiteses integralas tetelenek felhasznalasaval belathato, hogy ez az integral fuggetlen a parametertezestol, ha azok ugyanazt az iranyitast hatarozzak meg.
Megj. A kiszamitasi formulaban skalarvaltozos vektorerteku fuggveny integralja szerepel. Ezt a kovetkezokeppen kell kiszamitani:
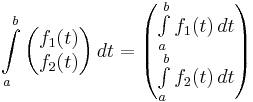
Visszavezetés valós vonalintegrálra es feluleti integralra
Az integrál kifejezhető vonalintegrállal. Ha ugyanis f= u + iv, akkor az f=(u,v) vektormezőnek olyan differenciálforma szerinti integrálja a komplex pályamenti integrál, mely az f=(u,v) vektor és a dz=(dx,dy) infinitezimális elmozdulásvektor komplex szorzásaként jön létre:
Ebben a felírásban az (u,-v) és (v,u) olyan segédvektormezők, melyek vonalintegráljai adják meg a komplex integrál valós és képzetes részét. Tehát az integrált a
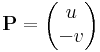 és
és 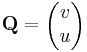
segédvektormezők síkbeli vonalintegráljai
vagy
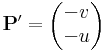 és
és 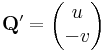
segédvektormezők síkbeli felületi integráljai
szolgáltatják.
Itt érdemes feleleveníteni, hogy az v = (v1, v2) síkvektormező vonalintegrája a v1dx+v2dy differenciálforma integrálja az L görbére, felületi integrálja a (v1, v2)(df1, df2)=v_1df_1+v_2df_2 "differencialforma" integralasa adja. Itt az infinitezimalis feluletelem (df1, df2)=(dy,-dx):
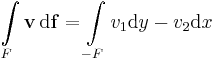 ,
,
Ahol az F irányítását megváltoztattuk F'=-F-re, amikor vonalintegrálra tértünk át.
Primitívfüggvény
A G: [a,b]  C görbe zárt görbe, ha G(a)=G(b). A zárt görbére vett integrál a körintegrál.
C görbe zárt görbe, ha G(a)=G(b). A zárt görbére vett integrál a körintegrál.
Az első eszköz a Newton--Leibniz-formulából következik, hisz ha F'=f, akkor ∫zw f = F(w) - F(z).
Tétel. Ha a D tartományon értelmezett f függvénynek van primitív függvénye, akkor a körintegrál minden a D-ben haladó zárt görbén eltűnik:
Példa. Az 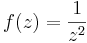 -nek van primitívfüggvény, így körintegrálja mindenütt eltűnik.
-nek van primitívfüggvény, így körintegrálja mindenütt eltűnik.
Példa. Paraméteresen kiszámolható, hogy
akrámilyen r > 0 sugárra. Tehát a teljes C \ {0}-n a reciproknak nincs primitívfüggvénye. (De egyszeresen összefüggő, a 0-t nem tartalmazó tartományon már van: a logaritmus.)
A komplex analízis főtétele
A komplex N--L-tétel nem túl hatékony eszköz. A N--L-tétel síkvektoranalízisbeli általánosításához kell folyamodnunk, például a Stokes-tételhez, ha többet akarunk mondani:
Stokes-tétel (R2-re) Legyen a D síkbeli tartomany határa a ∂D zárt görbe, megfelelően irányítva. Ha v folytonosan R-differenciálható egy nyílt halmazon, mely tartalmazza D lezártját, akkor
Ekkor csak a rotációt kell kiszámítanunk:
Ami, a C-R-egyenletek miatt igaz.
Innen
Goursat ennél is mélyebb eredményt talált:
Goursat-lemma. A T háromszöglapon reguláris f komplex függvény integrálja a háromszög határán nulla:
Bizonyitas. A haromszoget osszuk fel 4 egybevago haromszogre: Δ=Δ1∪Δ2∪Δ3∪Δ4. Ha jol iranyitjuk a kis haromszogek hatarat, akkor
Ezt felulbecsulhetjuk a kovetkezovel:
most Δ(1)-et bontjuk fel es folytatva a felosztast egy nullahoz tarto nagysagu haromszogekbol allo egymasba skatulyazott (Δ(n)) haromszogsorozatot kapunk, mely egy ponthoz, a z0-hoz tart. A haromszogek kerulete K/2n, ha K az eredeti haromszog kerulete. Erra a sorozatra tovabba:
igaz.
Most felhasznaljuk a komplex differencialhatosagot. Tetszoleges ε>0 szamra van olyan kornyezete z0-nak, es a haromszogsorozatnak olyan N indexe, melyre az n-edik tagok mar a kornyezetben vannak es az alabbi formulaban az |ε(z)|<ε:
Ezt integralva a haromszogre:
Itt az utolso kifejezest az ivhossz integrallal felulbecsuljuk:
Mivel ε tetszoleges volt, ezert az integral eltunik.
Innen már könnyen adódik a komplex analízis főtétele, melyet először Cauchy modott ki ugyan csak folytonosan diffható komplex függvényre, de Goursat ezt megfejelte a gyengített feltételével:
Főtétel. Ha a D egyszeresen összefüggő tartományon reguláris az f komplex függvény, akkor a tartományban minden zárt G egyszeru görbén a függvény integrálja nulla:
Cauchy-formulák
A Cauchy-formulák azért múlhatatlan fontosságúak, mert ezeknek következménye, hogy egy reguláris függvény nem csak egyszer, de végtelenszer differenciálható, sőt analitikus.
Tétel. Ha f az z_0 egy U környezetén reguláris, akkor tetszőleges az U-ban haladó, a z_0-t egyszer körülhurkoló pozitívan irányított G zárt görbére:
Riemann-tétel
Tétel. Legyen U nyilt tartomány, z0 ∈ U. Ha f az U\{z0}-on reguláris és korlátos, akkor minden U-beli körintegrálja eltűnik.
Bizonyítás. Belátjuk, az f Laurent-sora csak reguláris részből áll a z0 körül. Az Laurent-sor együtthatóformuláiból, k < 0 egészre és Kr r sugarú körre:
hiszen f korlátjához létezik olyan kis környzet, ahol a nullához tartó második tényező K-nál kisebb (vagy 1, és akkor a képletben és a végeredméybencsak K szerepel). Ha pedig r-rel tartunk a 0-hoz, az együttható eltűnik.
f-tehát kiterjeszthető U-n reguláris függvénnyé, így a Cauchy-tétel miatt minden körintegrálja eltűnik. Vagy egyszerűbben: f reziduuma a megszüntethető szingularitási helyen 0.
Reguláris függvény analitikus, Laurent-sorfejtés
Tétel. -- A Laurent-sor tétele -- Ha az f: C  C és a ∈ C szám és 0 ≤ r < R ≤ +∞ olyan sugarak, hogy f az
C és a ∈ C szám és 0 ≤ r < R ≤ +∞ olyan sugarak, hogy f az
nyílt körgyűrűben reguláris, akkor egyértelműen léteznek olyan (cn)n∈Z komplex számok, éspedig tetszőleges a T-ben haladó az a-t egyszer pozitív irányban körbehurkoló G görbére:
hogy a
függvénysor konvergens T-ben és minden z ∈ T számra:
Bizonyítás. f-et most nem tudjuk előállítani a Cauchy-integrálformulával, mint a Taylor-sor esetén, mert az a pontban esetleg a függvény nem reguláris. De előállíthatjuk két hasonló formula különbségeként.
Rögzítsük egy tetszőlegesen választott z ∈ T-t. Legyenek k1 és k2 két a középpontú, T-ben haladó, pozitívan irányított kör, úgy, hogy z a k1 és k2 körök közötti nyílt tartományba essen. Ezekből a körökből és az őket elválasztó gyűrűt sugárirányban befelé átmetsző s szakaszból elkészítünk egy olyan zárt görbét, melyre már alkalmazható az integrálformula. Tekintsük úgy, hogy k1 kezdő és végpontja az s kezdőpontja, k2 kezdő és végpontja pedig az s végpontja. Legyen
itt (-s) az s-sel ellenkező irányítású szakaszt jelzi. Ekkor Γ a z-t egy reguláris tartományban hurkolja egyszer, pozitívan körbe, így a Cauchy-integrálformulával:
Node, ebben az integálban az s íven kétszer oda-vissza végezzük el az integrálást, így az erre vett integrál eltűnik. Másrészt a (-k2)-n vett integrál ellenkezője a 'k2-vettének, így végülis:
Hangsúlyozzuk, hogy z és a most konstansok, így a
az értelmezési tartományán analitikus függvény. Ennek -- szikásos módon a mértani sor összegére vonatkozó képlet segítségével -- elvégezhetjük az a középpontú, valamilyen körön belüli hatványsorba fejtését. Természetesen a |w-a| < |z-a| feltételt meg kell követelnünk, hiszen hatványsor konvergenciakörében nem lehet benne a z szakadási pont. Tegyük fel tehát, hogy |w-a| < |z-a|. Ekkor:
Ezzel megvan a sorfejtés minden együtthatója, ugyanis 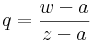 -ra kell alkalmazni a mértani sor formuláját:
-ra kell alkalmazni a mértani sor formuláját:
1) Világos, hogy ezt a sorfejtést csak a k2-re vonatkozó integrálban használhatjuk fel, mert ott lesz a q < 1 (ill. a w mindig közelebb a-hoz mint z-hez). Ezt az integrált tehát:
az integrál felcserélhető a szummával és a w-től független tagok kihozhatók az integrál elé, ezért
Ekkor egy konvergens, negatív kitevőjű hatványsort kaptunk, melynek csak főrésze van, de érdekes módon nem a középponttal és w-re, hanem a középponttal és z-ra. Ez pont a kívánt sorfejtés, melyet érdemes átindexelni úgy, hogy a szummázás -1-től induljon és -∞-ig menjen:
Már csak azt kell megmagyaráznunk, hogy a k2 helyére most már minden olyan G görbére felírható, mely az a-t pozitívan öleli körbe egyszer és a regularitási tartományban halad. Valóban, a képletbeli integrál már független az 1/(w-z) sorfejtési szituációjától és minden olyan G görbére áttranszformálható melyek folytonosan áttranszformálható k2-be. Ez a T körgyűrű összes a tételi állításban megadott görbéjére áll.
2) Most már az előző számolásból sejthető, hogy a Laurent-sor reguláris része akkor jön ki, ha az 1/(w-z) reciprokfüggvényt a az a körül nem pozitív, hanem negatív kitevőjű hatványsorba, fejtjük -- mint az első példában. Ezt a |w-a| > |z-a| feltétellel tehetjük csak meg, hisz ilyen sor konvergenciatartománya körgyűrű és a z szinguláris pontot nem tartalmazhatja:
Ez a sor valóban akkor konvergens, ha |w-a| > |z-a|. Ezzel az előző pomt számolását elvégezve az f(z)-t előállító Laurent-sor reguláris részét kapjuk. QED
Következmény. Reguláris függvény analitikus.
Következmény. Az izolált szingularitások a sorfejtés szerint osztályozhatóak éspedig. Az f függvény a z0 izolált szinguláris pontja körüli sorfejtésében
- pontosan akkor van csak reguláris tag, ha a szingularitás megszűntethető,
- pontosan akkor van véges sok főrészbeli tag, ha végtelen a határérék z0-ban,
- pontosan akkor van végtelen sok főrészbeli tag (lényeges szingularitás), ha nem létezik a határérék z0-ban.
Felületi integrál, Gauss-tétel
Definíció. Legyen 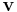 vektormező, mely
vektormező, mely 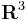 egy nyílt D tartományán értelmezett.
Legyen
egy nyílt D tartományán értelmezett.
Legyen 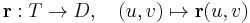 folytonosan differenciálható függvény, melynek értelmezési tartománya a T mérhető síktartomány. Ekkor a vektorfüggvény integrálját és létezését a felület mentén a következő limesszel definiáljuk:
folytonosan differenciálható függvény, melynek értelmezési tartománya a T mérhető síktartomány. Ekkor a vektorfüggvény integrálját és létezését a felület mentén a következő limesszel definiáljuk:
Itt tehát T-t egymásba nem nyúló, mérhető Ii síktartományokra bontjuk fel, amelyek ármérője egyre csökken.
Az integrál létezésére és értékére az alábbi egyszerű kritériumot és tartományi integrált írhatjuk föl. Legyen 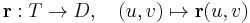 folytonosan differenciálható függvény, melynek értelmezési tartománya a T mérhető síktartomány. Ekkor az
folytonosan differenciálható függvény, melynek értelmezési tartománya a T mérhető síktartomány. Ekkor az 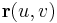 deriváltjai léteznek, a felületi integrál létezik és felírható
deriváltjai léteznek, a felületi integrál létezik és felírható
Ha a skaláris szorzat invariáns értelmezését vesszük, akkor a fenti formulát még a következőképpen is felírhatjuk:
ahol 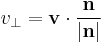 , azaz a felületi integrál egyenlő a vektormezőnek a felületi érintősík normálisa irányába eső előjeles komponense ugyanazon felületre vonatkozó felszín szerinti integráljával.
, azaz a felületi integrál egyenlő a vektormezőnek a felületi érintősík normálisa irányába eső előjeles komponense ugyanazon felületre vonatkozó felszín szerinti integráljával.
Megjegyzendő, hogy a képletben szereplő vegyes szorzat értéke 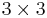 -as determinánsként számítható ki a komponenseiből:
-as determinánsként számítható ki a komponenseiből:
Tétel -- Gauss-Osztrogradszkíj -- Legyen 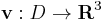 folytonosan differenciálható vektormező,
folytonosan differenciálható vektormező, 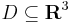 tartomány és legyen V a D-ben lévő mérhető térrész, melynek pereme az
tartomány és legyen V a D-ben lévő mérhető térrész, melynek pereme az 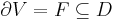 zárt felület a térrészből kifelé mutató irányítással. Ekkor
zárt felület a térrészből kifelé mutató irányítással. Ekkor
A tétel fontos alkalmazása a gömbszimmetrikus vektormezők felületi integráljának kiszámítása, ezek közül is a legfontosabb a reciproknégyzetes erősségű vektormezők.
Számítsuk ki a
vektormező integrálját a tetszőleges Γ zárt felületre, mely az origót belsejében tartalmazó V kompakt tartomány pereme, kifelé irányítva!
Először kiszámítjuk a vektoremző divergenciáját ott, ahol értelmezve van:
Itt felhasználtuk a divergenciára vontkozó szorzási szabályt.
Az integrál előállítható egy a v értelmezési tartományába eső tartomány peremére és egy másik felületre vonatkozó felületi integrálként. Legyen ugyanis G az origó középpontú olyan R sugarú gömb, mely benne van V belsejében és D az a tartomány pedig legyen V minusz G. Ekkor
azaz
Tehát csak G határára kell kiszámítani a vektormező fluxusát. Ezt az invariáns formulával tesszük:
(Imént lényegében az elektrosztatikus Gauss-törtvény állítását vezettük le a Coulomb-törvényből)
Vonalintegrál, Stokes-tétel
Legyen 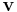 vektormező, mely
vektormező, mely 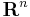 egy nyílt D tartományán értelmezett.
Legyen
egy nyílt D tartományán értelmezett.
Legyen ![\Gamma:[a,b]\to D,\quad t\mapsto\mathbf{r}(t)](/upload/math/9/c/9/9c9b8d9ae983dda27addd8193049f81d.png) folytonosan differenciálható függvény. Ekkor a vektormező integrálját és létezését a görbe mentén a következő limesszel definiáljuk:
folytonosan differenciálható függvény. Ekkor a vektormező integrálját és létezését a görbe mentén a következő limesszel definiáljuk:
Az integrál létezésére és értékére az alábbi egy egyszerű kritériumot és egydimenziós integrált írhatjuk föl. Legyen ![G:[t_1,t_2]\to D,\quad t\mapsto\mathbf{r}(t)](/upload/math/3/4/5/34514e0db5f87a8ae0ea298f26dcb8f9.png) legfeljebb véges sok pontban nem folytonosan differenciálható függvény. Ekkor az
legfeljebb véges sok pontban nem folytonosan differenciálható függvény. Ekkor az 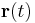 deriváltja véges sok pont kivételével létezik, a vonalintegrál létezik és felírható
deriváltja véges sok pont kivételével létezik, a vonalintegrál létezik és felírható
Ha a skaláris szorzat invariáns értelmezését vesszük, akkor a fenti formulát még a következőképpen is felírhatjuk:
ahol 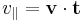 , azaz a vektormezőnek a görbe érintője irányába eső előjeles vetülete.
, azaz a vektormezőnek a görbe érintője irányába eső előjeles vetülete.
Tétel -- Stokes-tétel -- Legyen 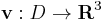 folytonosan differenciálható vektormező,
folytonosan differenciálható vektormező, 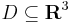 tartomány és legyen
tartomány és legyen 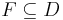 irányított, peremes felület, ennek pereme
irányított, peremes felület, ennek pereme 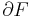 . Ekkor
. Ekkor
Megjegyezzük, hogy a perem irányítása kompatibilis kell hogy legyen a felület irányításával, ellenkező esetben az integrál a fenti ellentettje lesz. Kompatibilis a felület és a pereme irányítása, ha "a felületi normálvektor irány a fejünk iránya, a lábunk a felületen van, a peremen haladunk végig és a felület bal kéz felől esik (jobbkézszabály)".
A tétel alkalmazására a következő hengerszimmetrikus esetet nézzük.
Legyen
a vektormező és a felület az [xy] sík egy olyan tetszőleges T mérhető tartománya, mely a belsejében tartalmazza az origót és a pereme a G zárt görbe. Igazoljuk ekkor, hogy G-re az integrál 2π.
Először kiszámítjuk a vektromező rotációját. Ehhez felhasználjuk a rotációra vonatkozókövetkező azonosságot:
A rotáció a deriválttenzor vektorinvariánsának kétszerese, mivel lineáris leképezés deriváltja saját maga, ezért a képletbeli rotáció 2k. A képletbeli gradiens alatti skalármező a tengelytől mért távolságtől függ, ezért:
Most felbontjuk a T tartományt egy D lyukas tartományra és egy körlapra. A K körlap sugara legyen olyan R, mely esetén a körlap a T belsejében van benne. Ekkor
Tehát
Innen a vonalintegrál invariáns értelmezése folytán:
(Itt lényegében a végtelen hosszú egyenes vezető körüli görbén a mágneses indukció körintegrálját határoztuk meg.)
CROSS és alkalmazása és a Green-tétel
Definíció. A kettő vagy háromdimenziós térben CROSS a következő lineáris ill. bilineáris leképezés:
Ha 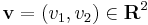 , akkor
, akkor  .
.
Ha 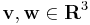 , akkor
, akkor 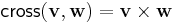 .
.
Leképezések invariánsai
Az S lineáris leképezés szimmetrikus, ha minden ortonormált bázisban a mátrixa szimmetrikus mátrix. Igaz az, hogy S pontosan akkor szimmetrikus, ha minden u, v vektorra
- u
 (Sv)=v
(Sv)=v (Su),
(Su),
ahol  a skaláris szorzás.
a skaláris szorzás.
Az A lineáris leképezésantiszimmetrikus, ha minden ortonormált bázisban a mátrixa antiszimmetrikus mátrix. Igaz az, hogy A pontosan akkor antiszimmetrikus, ha minden u, v vektorra
- u
 (Av)=-v
(Av)=-v (Au),
(Au),
ahol  a skaláris szorzás.
a skaláris szorzás.
Bármely T lineáris leképezés egyértélműen előáll S + A alakban, ahol S szimmetrikus, A pedig antiszimmetrikus, éspedig:
Két fontos tétel:
Tétel -- Ha A ∈R3 (illetve R2 ) antiszimmetrikus, akkor létezik olyan a vektor (vagy a skalár), hogy minden v vektorra:
a-t (ill. a-t) az A vektorinvariánsának nevezzük (bár a síkon ez skalár). A tételt elég a sztenderd bázisban igazolni, ott az a×( . ) opertátorral, azonos így A ez az operátor.
Főtengelyétel -- Ha S ∈Rn×n szimmetrikus, akkor minden sajátértéke valós és létezik a sajátvektorokból álló B ortonormált bázis, amiben S főtengelyre transzformálható, azaz diagonális és az elemei az S sajátértékei:
Ez nehéz, de fontos tétel.
A deriválttenzor invariánsai
Tudjuk, hogy ha v differenciálható vektorfüggvény, akkor az r0 pontbeli differenciálján, vagy deriváltján, vagy deriválttenzorán azt az egyértelműen létező A lineáris leképezést értjük, melyre:
Minthogy az A deriválttenzor lineáris leképezés, ezért érdemes külön elnevezni az invariánsait (h tetszőleges vektora a térnek):
azaz A vektorinvariánsának duplája a rotáció.As a derivált leképezés szimmetrikus része. A divergencia a skalárinvariáns:
Világos, hogy ebből úgy lesznek a parciális deriváltakkal definiált alakok, ha az A sztenderd bázisbeli mátrixát, azaz a J Jacobi mátrixot írjuk fel. Ekkor mindkét említett differenciáloperátort a szokásos alakjában kapjuk:
Integrálok kiszámítási formulái
Felszín szerinti intergálok:
Síkban: 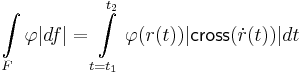
Térben: 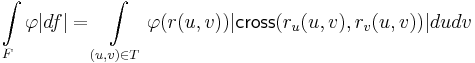
Felületmenti intergálok:
Síkban: 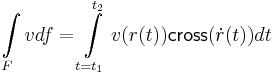
Térben: 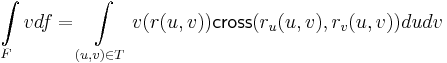
Síkban a felületi és felszín integrál kifejezhető az ívhossz és a vonalintegrállal, a következőképpen. Mivel 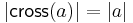 , ezért
, ezért
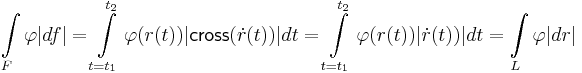 ,
,
ahol L és F paraméterezése 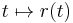 ugyanaz.
ugyanaz.
Felületi integrál esetén, ha F egy T tartomány peremdarabja, akkor
ugyanis felhasználva, hogy cross(dx,dy)=(-dy,dx) és cross(v1,v2)=(-v2,v1)
Itt -F, mint vonal a T tartomány peremének egy darabja, amint pozitívan van irányítva (ha tudjuk, hogy F kifelé irányított)
Green-tétel
Legyen a (P,Q) síkbeli vektormező egy U nyílt halmazon folytonosan differenciálható és legyen T az U egy kompakt mérhető része, ∂T a peremét alkotó görbe. Ekkor
Ezt a tételt egy spéci T háromszöglapra bizonyítjuk. Legyen
Az így definiált T az x tengelyre vonatkozóan normáltartomány. A bizonyításban szükség lesz arra, hogy T-t y tengelyre vonatkozó normáltartományként is megadjuk:
Határa:
A vonaldarabok paraméterezése legyen rendre: (t,0), ha t∈[0,1], (t,1-t), ha t∈[0,1] (ennek az irányításét majd meg kell fordítani) és (0,t), t∈[0,1] (ennek is meg kell fordítani). Ekkor
Itt végeztünk egy paramétercserét.
Ezután pedig felhasználjuk, hogy a két integrál ugyanarra a tartományra vett kettősintegrál:
A tétel érvényes minden n-szeresen összefüggő tartományra is (az n-1 db lyukat tartalmazó kilyukasztott körlappal homeomorf tartományokra), mert egyfelől változatlan marad, ha görbevonalú háromszögre térünk át (integráltranszformációval), másfelől minden n-szeresen összefüggő tartomány felbontható véges sok görbevonalú háromszögre, ahol az integrálok összegében a belső szakaszok eltűnnek és a tétel szintén érvényben marad.
A Green-tétel a (háromdimenziós) Stokes-tétel speciális esete, hiszen a (P,Q,0) vektormező rotációja pont (0,0,∂xQ-∂yP). A Green-tételből levezethető a kétdimenziós Gauss-tétel, a következőképpen. Legyen T a síkbeli peremes tartomány és ∂T a pereme mint pozitívan irányított zárt görbe (ill. véges sok görbe diszjunkt úniója, ha n-szeresen összefüggő, n>1). Ekkor a Q:=P, P:=-Q szereposztással felírva a Green-tételt:
Itt a baloldali integrandus a (P,Q) vektormező cross-ja, ami viszont a ∂T-re, mint valódi felületre vett integrál ellenkezője:
ahol persze ∂xP+∂yQ=div(P,Q) és a -∂T valódi felület a tartományból kifelé van irányítva.
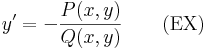
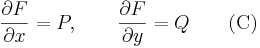
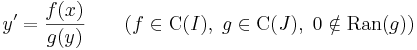
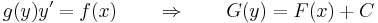
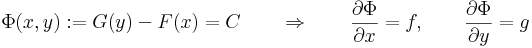
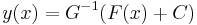
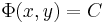
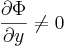
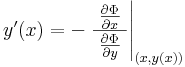
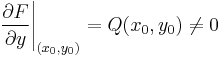
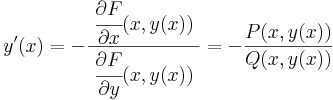
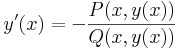
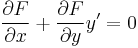
![(F(x,y(x)))'=[\mathrm{grad}\,F|_{(x,y(x))}]\cdot\begin{bmatrix}x'\\y'(x)\end{bmatrix}=\frac{\partial F}{\partial x}|_{(x,y(x))}+y'\frac{\partial F}{\partial y}|_{(x,y(x))}\equiv 0\,](/upload/math/6/a/0/6a01c3a741e5c2d447b6e0254117aa36.png)
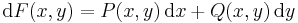
![[\mathrm{d}F(x,y)]=\mathrm{grad}\,F(x,y)=\left[\;\frac{\partial F}{\partial x}\;,\;\frac{\partial F}{\partial y}\;\right]](/upload/math/6/d/6/6d677f005d45feb13decbeb9f8433c81.png)
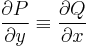
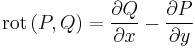
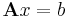
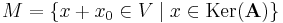
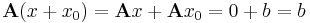
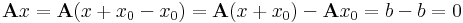
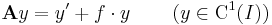
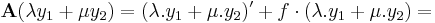
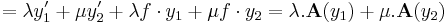


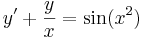
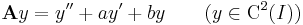
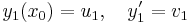
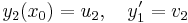
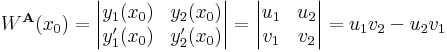
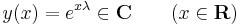
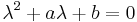
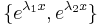
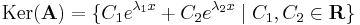
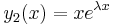
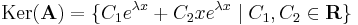



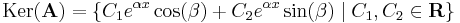
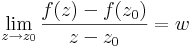
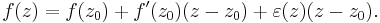

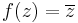
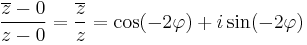
![\lim\limits_{z\to z_0}\frac{f(z)-f(z_0)-[w]\cdot (z-z_0)}{|z-z_0|}=0](/upload/math/c/1/0/c10238bb240c0184bbeacdb2af1ba696.png)
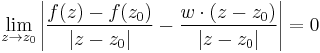
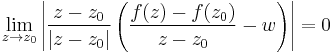
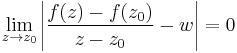
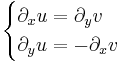
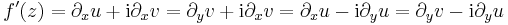
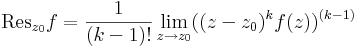
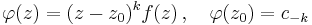
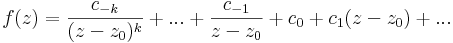
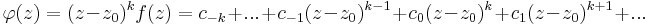
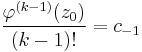
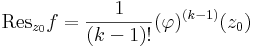
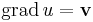
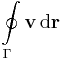
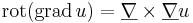
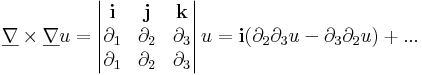
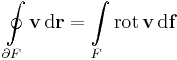
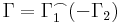
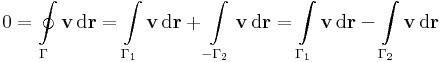
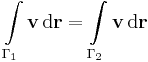
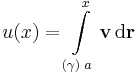
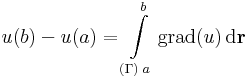
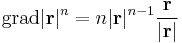
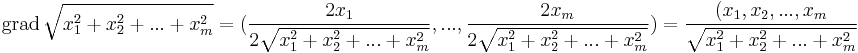
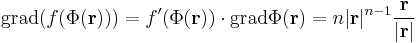
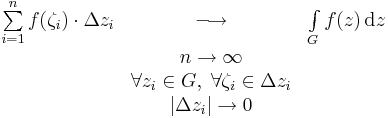
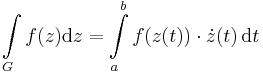
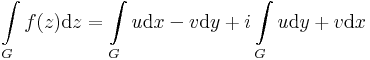
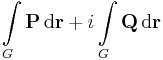
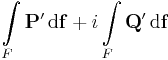
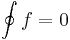
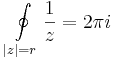
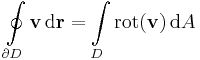
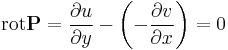
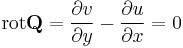
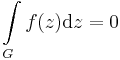
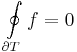
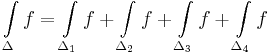
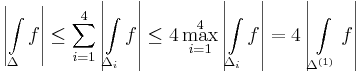
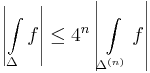
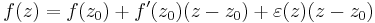
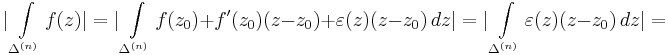
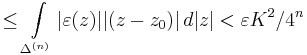
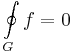
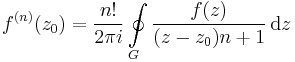
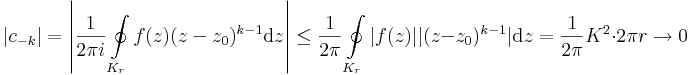
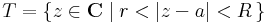
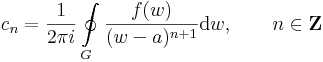
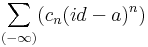
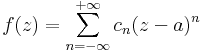
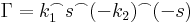
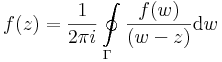
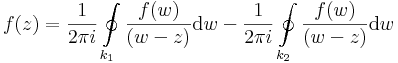
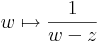
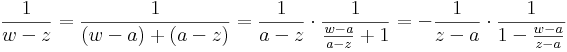
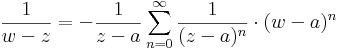
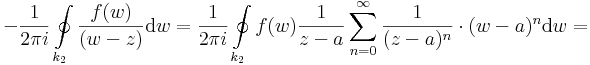
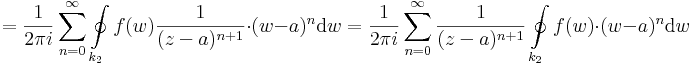
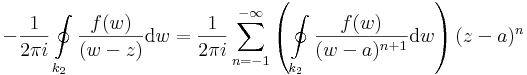
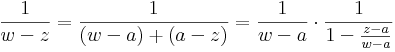
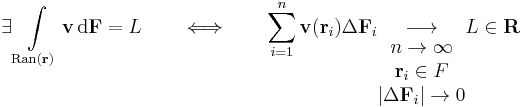
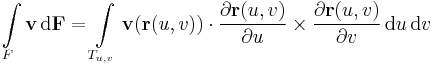
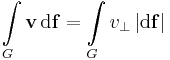
![\mathbf{v}(\mathbf{r}(u,v))\cdot \frac{\partial \mathbf{r}(u,v)}{\partial u}\times\frac{\partial \mathbf{r}(u,v)}{\partial v}=\begin{vmatrix}\quad[\mathbf{v}(\mathbf{r}(u,v))]\quad\\\\
\left[\frac{\partial \mathbf{r}(u,v)}{\partial u}\right]\\\\
\left[\frac{\partial \mathbf{r}(u,v)}{\partial v}\right]\end{vmatrix}](/upload/math/2/c/3/2c3bee39da44a162adadf93d7dfbc939.png)
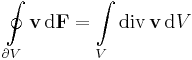
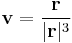
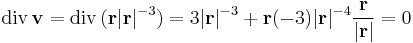
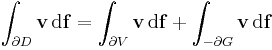
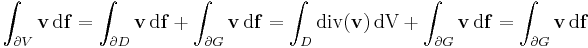
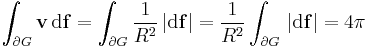
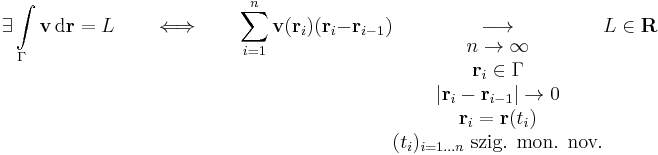
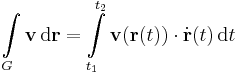
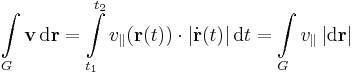
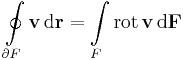
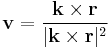
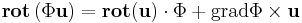
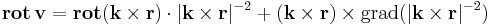
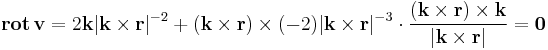
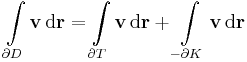
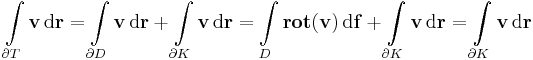
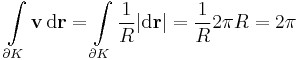
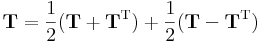

![[\mathbf{S}]_{\{\mathbf{v}_1,...,\mathbf{v}_n\}}=\begin{pmatrix}\lambda_1& 0& 0\\
0& \ddots& 0\\
0 & 0& \lambda_n\end{pmatrix}](/upload/math/2/b/6/2b6d68afeb211967e07984838ae5f4a1.png)
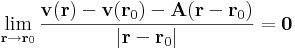
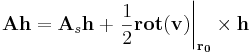

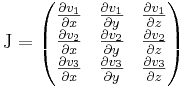
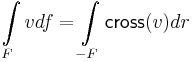
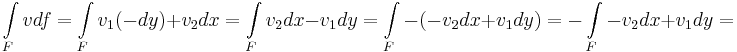
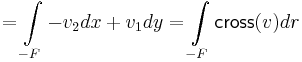
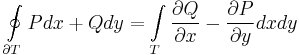
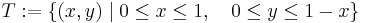
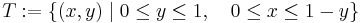
![\partial T=[(0,0),(1,0)]\cup[(1,0),(0,1)]\cup[(0,1),(0,0)]](/upload/math/a/0/3/a03659af9dcfd03efebae925bc000c8c.png)