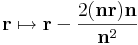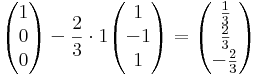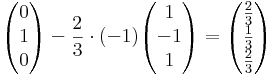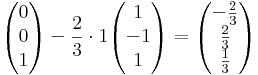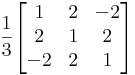Szerkesztő:Mozo/egyéb
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) (→Tükrözés síkra) |
Mozo (vitalap | szerkesztései) (→Tükrözés síkra) |
||
| 1. sor: | 1. sor: | ||
==Tükrözés síkra== | ==Tükrözés síkra== | ||
| − | '''Példa.''' Tekintsük az S = {(x,y,z) ∈ '''R'''<sup>3</sup> | x-y+z=0 } síkot. Adjuk meg az S síkra történő tükrözés mátrixát, a sajátvektorait és a sajátaltereket, | + | '''Példa.''' Tekintsük az S = {(x,y,z) ∈ '''R'''<sup>3</sup> | x-y+z=0 } síkot. Adjuk meg az S síkra történő tükrözés mátrixát, a sajátvektorait és a sajátaltereket, illetve a sajátkoordinátarendszert! |
A síkra tükrözés hozzárendelési utasítása: | A síkra tükrözés hozzárendelési utasítása: | ||
| 8. sor: | 8. sor: | ||
:<math>\begin{pmatrix}0\\1\\0\end{pmatrix} - \frac{2}{3}\cdot (-1)\begin{pmatrix}1\\-1\\1\end{pmatrix}=\begin{pmatrix}\frac{2}{3}\\\frac{1}{3}\\\frac{2}{3}\end{pmatrix}</math> | :<math>\begin{pmatrix}0\\1\\0\end{pmatrix} - \frac{2}{3}\cdot (-1)\begin{pmatrix}1\\-1\\1\end{pmatrix}=\begin{pmatrix}\frac{2}{3}\\\frac{1}{3}\\\frac{2}{3}\end{pmatrix}</math> | ||
:<math>\begin{pmatrix}0\\0\\1\end{pmatrix} - \frac{2}{3}\cdot 1\begin{pmatrix}1\\-1\\1\end{pmatrix}=\begin{pmatrix}-\frac{2}{3}\\\frac{2}{3}\\\frac{1}{3}\end{pmatrix}</math> | :<math>\begin{pmatrix}0\\0\\1\end{pmatrix} - \frac{2}{3}\cdot 1\begin{pmatrix}1\\-1\\1\end{pmatrix}=\begin{pmatrix}-\frac{2}{3}\\\frac{2}{3}\\\frac{1}{3}\end{pmatrix}</math> | ||
| + | A mátrix: | ||
| + | :<math>\frac{1}{3}\begin{bmatrix} | ||
| + | 1 & 2 & -2\\ | ||
| + | 2 & 1 & 2\\ | ||
| + | -2 & 2 & 1 | ||
| + | \end{bmatrix}</math> | ||
| + | ez -1 determinánsú szimmetrikus mátrix, ortonormált vektorokból álló sajátrendszerrel, | ||
A lap 2008. március 10., 15:25-kori változata
Tükrözés síkra
Példa. Tekintsük az S = {(x,y,z) ∈ R3 | x-y+z=0 } síkot. Adjuk meg az S síkra történő tükrözés mátrixát, a sajátvektorait és a sajátaltereket, illetve a sajátkoordinátarendszert!
A síkra tükrözés hozzárendelési utasítása:
ahol n a sík normálvektora, itt (1,-1,1). A bázisok képei:
A mátrix:
ez -1 determinánsú szimmetrikus mátrix, ortonormált vektorokból álló sajátrendszerrel,