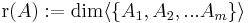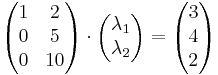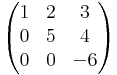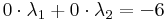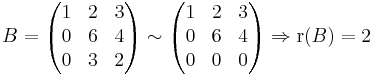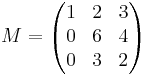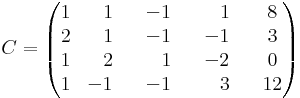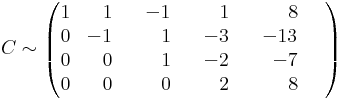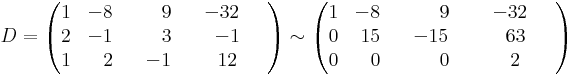Mátrix rangja

Egy n × m-es mátrix rangján a mátrix oszlopai által kifeszített Rⁿ-beli altér dimenzióját értjük. A mátrix rangja tehát k, ha oszlopai közül kiválasztható k db lineárisan független, de k + 1 db már nem.

Definíció

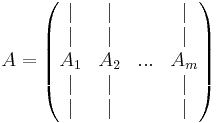
Ha tehát az A ∈ R^n×m mátrix alakja:

$A = \begin{pmatrix} \begin{matrix}\vert \\ \vert \\ A_1 \\ \vert \\ \vert \end{matrix}& \begin{matrix}\vert \\ \vert \\ A_2 \\ \vert \\ \vert \end{matrix} & ... & \begin{matrix}\vert \\ \vert \\ A_m \\ \vert \\ \vert \end{matrix} \end{pmatrix}$

ahol A₁, A₂, ..., A_m az oszlopai, akkor

$\mathrm{r}(A):=\mathrm{dim}\langle\{A_1,A_2,...A_m\}\rangle$

ahol

$\langle\{A_1,A_2,...A_m\}\rangle$

jelöli az oszlopvektorok által kifeszített (generált) alteret.

Példák

1.

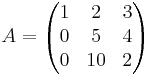$A = \begin{pmatrix} 1 & 2 & 3 \\ 0 & 5 & 4 \\ 0 & 10 & 2 \end{pmatrix}$ ekkor $\mathrm{r}(A):=\mathrm{dim}\left\langle \begin{pmatrix}1\\0\\0\end{pmatrix},\begin{pmatrix}2\\5\\10\end{pmatrix},\begin{pmatrix}3\\4\\2\end{pmatrix}\right\rangle$

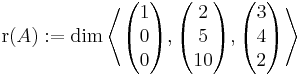
Világos, hogy az első két vektor független rendszert alkot, tehát r(A) legalább 2 (és legfeljebb 3, mert ilyen hosszúak). A kérdés, hogy a harmadik kifejezhető-e az első kettő lineáris kombinációjaként, azaz megoldható-e az

$\begin{pmatrix} 1 & 2 \\ 0 & 5 \\ 0 & 10 \end{pmatrix}\cdot \begin{pmatrix} \lambda_1 \\ \lambda_2\end{pmatrix}=\begin{pmatrix} 3 \\ 4 \\ 2 \end{pmatrix}$

egyenletrendszer (λ₁,λ₂)-re? Akibővítet mártix maga az A. Ebből Gauss-eliminációval (a középső kétszeresét kivonjuk a legalsóból)

$\begin{pmatrix} 1 & 2 & 3 \\ 0 & 5 & 4 \\ 0 & 0 & -6 \end{pmatrix}$

Az alsó sor így:

$0\cdot \lambda_1+0\cdot \lambda_2=-6$

aminek nincs megoldása. Tehát a harmadik oszlop nem fejezhető ki az első kettő lineáris kombinációjával, így függetlenek, ergó a rang 3.

Általánosan: ha az A n × n-es mátrixot Gauss-eliminálva háromszögmátrix jön ki, nemnulla főátlóbeli elemekkel, akkor A rangja a dimenzió: n.

2.

$B = \begin{pmatrix} 1 & 2 & 3 \\ 0 & 6 & 4 \\ 0 & 3 & 2 \end{pmatrix} \sim \begin{pmatrix} 1 & 2 & 3 \\ 0 & 6 & 4 \\ 0 & 0 & 0 \end{pmatrix} \Rightarrow \mathrm{r}(B) = 2$

mert alsó sor tiviálisan teljesül, a felső kettőból pedig kifejezhető λ₁, λ₂, éspedig: λ₂ = 4/6 = 2/3, λ₁ = 5/3 (és persze az első két oszlop független, mert a másodikat a 2 nemnulla miatt sehogyan se lehet kifejezni az elsőből ennek a két nullája miatt).

Sorrang és determinánsrang

A fenti fogalmaz oszloprangnak nevezzük. Belátható, hogy a függetlesn sorok maximális száma ugyanannyi, mint a független oszlopok maximális száma, azaz a sorrang egyenlő az oszlopranggal. Ebből az is következik, hogy

$A\in \mathbf{R}^{n\times m}\quad\Rightarrow\quad\mathrm{r}(A)\leq n \quad\mathrm{\acute{e}s}\quad \mathrm{r}(A)\leq m$

A számolásokban hasznos a következő tétel. Nevezzük egy tetszőleges mártix esetén aldeterminánsnak azt, hogy a mátrix tetszőleges négyzetes részmátrixának vesszük a determinánsát. Négyzetes részmátrixot úgy választunk ki, hogy vesszük a mátrix valamely k db oszlopát és k db sorát, és a metszéspontokban lévő elemekből alkotunk egy mátrixot. Az ilyet még k-adrendű minormátrixnak, determinánsát k-adrendű aldeterminánsnak is nevezzük. Ha a mátrix n × n-es kvadratikus, akkor maga is sajét maga egy (n-edrendű) minormátrixa. Ekkor

Tétel. Az A mátrix rangja az r szám, ha van r-edrendű nemulla aldeterminánsa, de nincs r + 1-ed rendű nemulla aldeterminánsa.

Ez utóbbi fogalmat determinánsrangnak nevezzük és mely atétel szerint egyezik a ranggal.

Példák

1.

$M=\begin{pmatrix} 1 & 2 & 3 \\ 0 & 6 & 4 \\ 0 & 3 & 2 \end{pmatrix}$

Tekintsük a determinánsrangot! A mátrixot az első oszlopa szerint kifejtve kapjuk, hogy det(M) = 1 $\cdot$ (6$\cdot$2 - 3$\cdot$4) = 0. Nincs tehát 3 × 3-as nemnulla aldeterminánsa. De a bal felső másodrendű aldetermináns a 6 ≠ 0, azaz van másodrendű, azaz r(M)=2.

2.

$C=\begin{pmatrix} 1 & 1 & -1\;\;\; & 1 & 8\\ 2 & 1 & -1\;\;\; & -1\;\;\; & 3\\ 1 & 2 & 1 & -2\;\;\; & 0\\ 1 & -1\;\;\; & -1\;\;\; & 3 & 12 \end{pmatrix}$

C rangja nyilván kisebb négynél, mert a sorok száma négy. A Gauss-eljárás azonnal megmondja, hány független oszlop van.

$C\sim\begin{pmatrix} 1 & 1 & -1\;\;\; & 1 & 8\\ 0 & -1\;\;\; & 1 & -3\;\;\; & -13\;\;\;\;\;\\ 0 & 0 & 1 & -2\;\;\; & -7\;\;\;\\ 0 & 0 & 0 & 2 & 8 \end{pmatrix}$

eszerint 4 független oszlop van (az ötödik már kifejezhető a többiből).

3.

$D=\begin{pmatrix} 1 & -8\;\;\; & 9 & -32\;\;\;\;\;\\ 2 & -1\;\;\; & 3 & -1\;\;\;\\ 1 & 2 & -1\;\;\;& 12\;\;\; \end{pmatrix} \sim \begin{pmatrix} 1 & -8\;\;\; & 9 & -32\;\;\;\;\;\\ 0 & 15\;\; & -15\;\;\;\;\; & 63\;\;\;\\ 0 & 0 & 0 & 2\;\;\; \end{pmatrix}$

Ez a lépcsős alak arról árulkodik, hogy az 1. 2. és 4. oszlop függetelen vektorrendszert alkot, miközben a 3. kifejezhető az első kettő lineáris kombinációjaként.