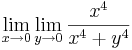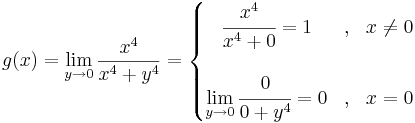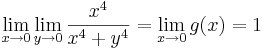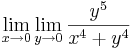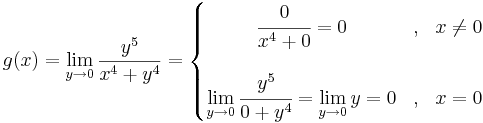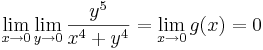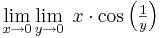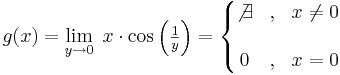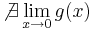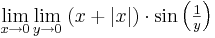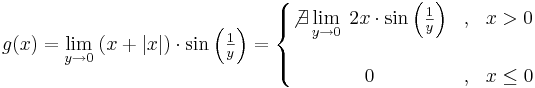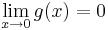Szerkesztő:Mozo/A2 feladatok
Tartalomjegyzék |
Gauss-elimináció-témakör
Paraméteres egyenletrendszer
Milyen a valós paraméterre oldható meg az alábbi egyenletrendszer?
Megoldás
Az A(a) x = b egyenletrendszer kibővített mátrixa és a Gauss-elimináció
x = b egyenletrendszer kibővített mátrixa és a Gauss-elimináció
Az egyenletrendszer akkor és csak akkor megoldható, ha a mátrix rangja egyenlő a kibővített mátrix rangjával. Világos, hogy
- r(A(a)) = 3, ha a ≠ 3 és
- r(A(a)) = 2, ha a = 3
Az első esetben a [A(a)|b] csak 3 lehet (csak három sora van), míg a másodikban [A(a)|b] rangja 3, mert három független oszlopvektor választható ki belőle (pl az első, a második és a negyedik). Tehát a ≠ 3 esetén lesz megoldása az egyenletrendszernek.
Megjegyzés. Úgy is fogalmazhatunk, hogy akkor és csak akkor van megoldás, ha az alsó sorban nem áll ellentmondás. Ez akkor van, ha az (a-3)z=-6-ból kifejezhetjük z-t, vagyis az a ≠ 3 esetén vagy ha az alsó sor 0 = 0 alakú, ami ugye nem áll.
Paraméteres mátrixrang
- Lásd az előző feladatot!
Lináris leképezés sajátértéke
Példa
Számítsuk ki az
mátrixú leképezés 111-edik hatványának sajátvektorait!
Megoldás
A bázisvektorok képei: (2,2) és (1,1), azaz mindkettőt az y = x egyenletű altérbe képezi az operátor. Világos, hogy ekkor a sajátaltér a μ.(1,1) alakú vektorok.
Példa
Számítsuk ki a x tengely körüli +36°-os forgatás 15-ödik és 17-edik hatványának sajátvektorait és sajátértékeit!
Megoldás
Ha A ez a lineáris operátor, akkor első hatványa a +36°-os forgatás, a második a 2 36°-os forgatás, ..., a 15-ödik hatványa a 15
36°-os forgatás, ..., a 15-ödik hatványa a 15 36°=360+180=180°-os forgatás.
Ennek sajátvektorai az x tengely vektorai, 1 sajátértékkel., De a 17-edik hatvány is csak egy forgatás, így ennek is ugyanezek lesznek a sajátvektorai (360°-nál már más lenne a helyzet, ott minden vektor fix).
36°=360+180=180°-os forgatás.
Ennek sajátvektorai az x tengely vektorai, 1 sajátértékkel., De a 17-edik hatvány is csak egy forgatás, így ennek is ugyanezek lesznek a sajátvektorai (360°-nál már más lenne a helyzet, ott minden vektor fix).
Függvényterek
Példa
Legyen L az R-en értelmezett valós függvények következő lineáris altere:
(azaz az exp(2 .), a sin(3
.), a sin(3 .) és a cos(3
.) és a cos(3 .) függvények által kifeszített altér.)
Adjuk meg L bázisát, igazoljuk, hogy
.) függvények által kifeszített altér.)
Adjuk meg L bázisát, igazoljuk, hogy
lineáris operátor és adjuk meg egy mátrixát!
Megoldás
boztosan generátorrendszere L-nek. Lássuk be, hogy B független. Tegyük fel ugyanis, hogy minden x valós számra
Ekkor x = 0-t véve:
illetve x = 2π-t véve is:
mely két egyenletet kivonva
azaz A = 0. Viszont ekkor C = 0-is teljesül és B csak nulla lehet, mert a szinuszfüggvény nem az azonosan nulla. Tehát a fenti egyenlőségnek csak triviális megoldása van A, B, C-ben.
Térjünk rá az operátor linearitására. A deriválás lineáris, a 4-gyel való szorzás lineáris és a leképezések összege lineáris, tehát A lineáris. Adjuk meg a mátrixot! A bázisok képei:
Így
Iterált határérték
Példa
Megoldás
Példa
Megoldás
Tehát g ≡ 0
Példa
Megoldás
Tehát g egyetlen pontból áll, éspedig a 0-nál 0. Ilyen (egypontú) függvények nincs határértéke:
Példa
Megoldás
Tehát g csak a nemnegatívokon értelmezett és ott 0:
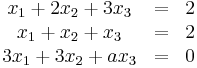
![[\mathbf{A}(a)|b]=\begin{bmatrix}
1 & 2 & 3 & 2 \\
1 & 1 & 1 & 2 \\
3 & 3 & a & 0
\end{bmatrix}\sim
\begin{bmatrix}
1 & 2 & 3 & 2 \\
0 & -1 & -2 & 0 \\
0 & -3 & a-9 & -6
\end{bmatrix}\sim
\begin{bmatrix}
1 & 2 & 3 & 2 \\
0 & -1 & -2 & 0 \\
0 & 0 & a-3 & -6
\end{bmatrix}](/upload/math/4/3/e/43e1d3c4eec1580b65f6e0a37bf42e54.png)
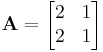
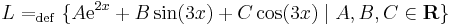
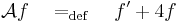
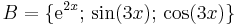
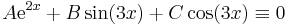
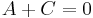
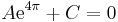
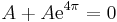
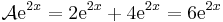
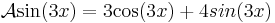
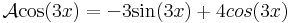
![[\mathcal{A}]=\begin{pmatrix}
6 & 0 & 0 \\
0 & 4 & -3 \\
0 & 3 & 4
\end{pmatrix}](/upload/math/3/e/2/3e28411c5eb10bb2a88d2c7ba8c6d76c.png)