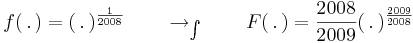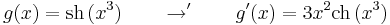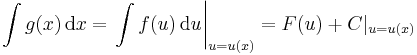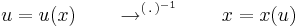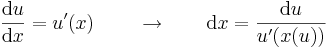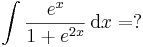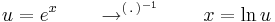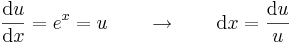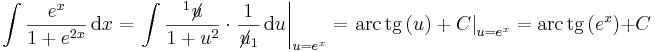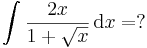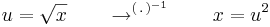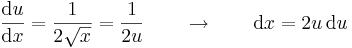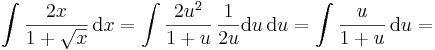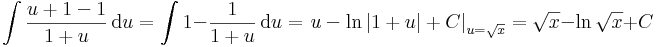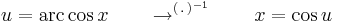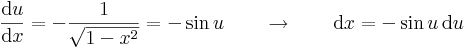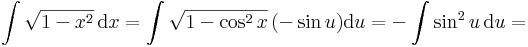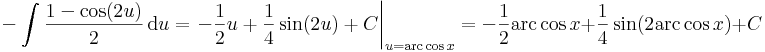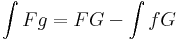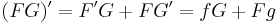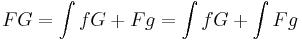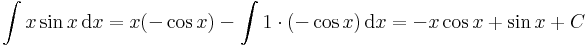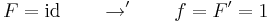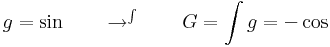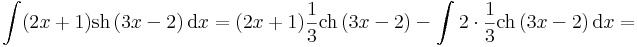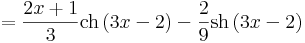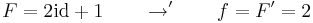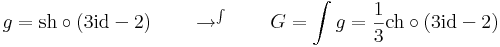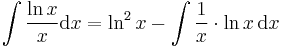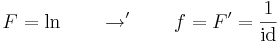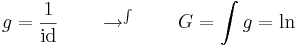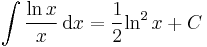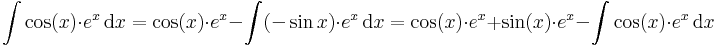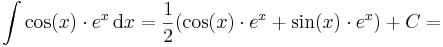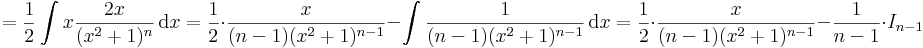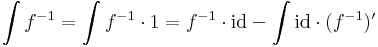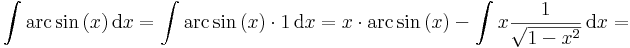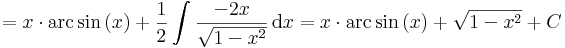Szerkesztő:Mozo/A2 szigorlat 13
Tartalomjegyzék |
Primitívfüggvény-keresés
Primitívfüggvény-keresésnek két metódusa van. Az egyik a helyettesítéses integrálás, a másik a parciális integrálás. Ezek előtt azonban egy triviális módszer, a deriválási táblázat megfodítása és az integrál eltolásinvarianciájának felhasználása. (Esetleg a lineáris argumentumú alapintegrál kiszámítása.)
Alapintegrálra visszavezethető integrálok
Ha tehát vesszük az elemi függvények és inverzeinek deriválási táblázatát, akkor jobbról balra olvasva megkapjuk az alapintegrálok táblázatát.
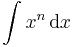
| 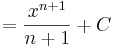
| 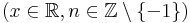
|
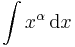
| 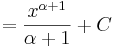
| 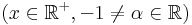
|
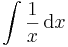
| 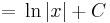
| 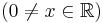
|
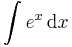
| 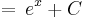
| 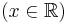
|
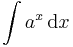
| 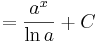
| 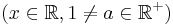
|
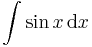
| 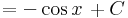
| 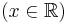
|
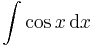
| 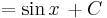
| 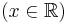
|
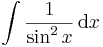
| 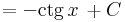
| 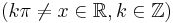
|
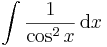
| 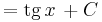
| 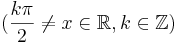
|
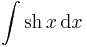
| 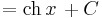
| 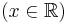
|
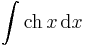
| 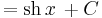
| 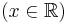
|
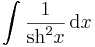
| 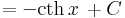
| 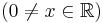
|
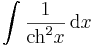
| 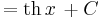
| 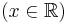
|
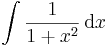
| 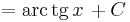
| 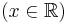
|
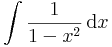
| 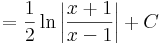
| 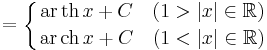
|
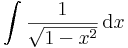
| 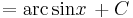
| 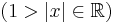
|
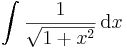
| 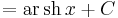
| 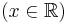
|
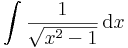
| 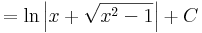
| 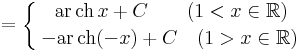
|
Alapintegrálok kiszámítása táblázatból
vagy a legkönnyebben elronthatók:
Alapintegrálok és eltolásinvariancia
Az integrál eltolásinvarianciáját használva:
Lineáris agrumentumú integrandus
A lineáris agrumentumúkra vonatkozó képlet:
ahol F'=f. Hiszen az összetett függvény deriválási szabálya szerint:
Ezzel pl:
Megjegyzés. Érdemes fejünkbe vésni a sin függvény deriváltajainak függvénysorozatát:
- sin
- cos
- − sin
- − cos
- sin
- cos

felfejé haladva integrálunk, lefelé haladva deriválunk.
pl.
Polinom/lineáris alak
itt már érdemes polinomosztással eljárni:
(x^2 + 2) : (x - 1) = x + 1
- x^2 - x
---------
x + 2
- x - 1
--------
3
Néha x2 + 1 nevezőjűre is működik:
Linearizáló formulák
Ezek arra alkalmasak, hogy a sin2, cos2, sh2. ch2 függvényeket (illetve alkalmasan megváltoztatott argumentumú változatukat) ki lehessen integrálni:
Mindezek a következők miatt állnak fenn:
ezért ezeket kivonva ill. összeadva, majd 2-vel elosztva a felső kettőt kapjuk. A másik kettő:
Itt érdemes megjegyezni az Osborne-szabályt: ha egy trigonometrikus azonosságban kicseréljük a megfelelő hiperbolikus függvényekre az összetevőket és minden olyan tag előjelét megváltoztatjuk, melyek két sh szorzatából állnak (speciálisan a sh2-ek elé egy - jelet teszünk), akkor megkapjuk a hiperbolikus azonosságot. Lásd: Osborne-szabály.
Ezek főleg határozott integráloknál adnak "szép" eredményt
Példa.
Helyettesítéses integrálás
Az első keresési eljárás az összetett függvény deriválási szabályának megfordításán alapul.
Tétel. Legyen g:I  J, F: J
J, F: J  R folytonosan differenciálható függvények és f: J
R folytonosan differenciálható függvények és f: J  R pedig olyan, hogy az F' = f, akkor az x
R pedig olyan, hogy az F' = f, akkor az x  f(g(x))
f(g(x))  g'(x)-nek is létezik primitív függvénye és
g'(x)-nek is létezik primitív függvénye és
Bizonyítás. A primitív függvény létezését az garantálja, hogy az integrandus folytonos.
Elegendő ellenőrizni, hogy x  F(g(x)) primitív függvénye x
F(g(x)) primitív függvénye x  f(g(x))
f(g(x))  g'(x)-nek, azaz az előbbi deriváltja az utóbbi:
g'(x)-nek, azaz az előbbi deriváltja az utóbbi:
QED.
...-alakú integrálok
Ebből a tételből származtathatjuk a "... alakú integrálokat":
Példák.
1.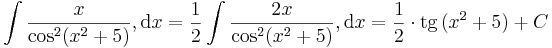 hiszen a "külső" függvény:
hiszen a "külső" függvény:
a "belső" függvény:
2.
hiszen a "külső" függvény:
a "belső" függvény:
3.
hiszen a "külső" függvény:
a "belső" függvény:
4.
hiszen a "külső" függvény:
a "belső" függvény:
Integrálás a helyettesítés elvégzésével
Megjegyzés. Intermezzóként megemlítjük, hogy a helyettesítés elnevezés abból fakad, hogy ekkor lényegében új ismeretlent vezetünk be. Persze az ezzel való számolás egy egészen más szemléletet igényel. A fő képlet ekkor:
ahol el kell végezni az
szimbolikus helyettesítést.
5. (exponenciális helyettesítés)
5. (gyökös helyettesítés)
6. (trigonometrikus helyettesítés)
Parciális integrálás
A helyettesításes integrálás a függvénykompozíció deriválására szolgáló képlet felhasználása volt primitívfüggvény keresésre. Most a szorzási szabályt fogjuk használni.
Tétel. Legyen f,g:[a,b]  R folytonos és F,G:[a,b]
R folytonos és F,G:[a,b]  R differenciálható olyan, hogy F' = f, G' = g. Ekkor az alábbi képletben szereplő összes integrandusnak létezik primitív függvénye és
R differenciálható olyan, hogy F' = f, G' = g. Ekkor az alábbi képletben szereplő összes integrandusnak létezik primitív függvénye és
Bizonyítás. Elég a bizonyítani, hogy a jobb oldal deriváltja a baloldali integrandus. Ehelyett egy kicsit másként csináljuk: belátjuk, hogy az FG függvény primitívfüggvénye az fG + Fg függvénynek, majd kefejezzük velőle a fenti formula baloldalát:
tehát
amiből már következik a fenti formula. QED.
Polinom szor exp, trig, hip
Az első alkalmazás az, amikor a egymás után parciális integrálásokkal polinommentes formulává alakítjuk az integrandust. Ekkor a fenti képlet F-je a polinom, amiből egyel alacsonyabb fokú polinomszoros integrandus keletkezik az ∫fG integrál esetén.
Hiszen
Egy hasonló:
Hiszen
Rekurziós integrálok, formulák
1.
az
szereposztással. A formulában visszatért a keresett integrál, így ezt kifejezve:
2.
amiből
tehát kétszeri parciális integrálással értük el.
3. Rekurziós formulát kapunk az alábbi In alakú integrálokra:
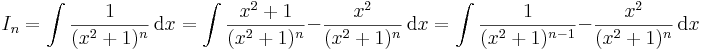 az utolsó tagot parciálisan integráljuk ki:
az utolsó tagot parciálisan integráljuk ki:
azaz In kifejezhető In − 1-segítségével.
Inverzfüggvények integrálja
Az
trükk sokszor alkalmas arra, hogy az inverz függvények integrálját parciálisan kiintegráljuk, hiszen az inverz függvények deriváltjának képlete az utolsó tényezőt a kezünkre játssza. Speciálisan a módszer alkalmas az összes ln, arc és ar függvény kiintegrálására.
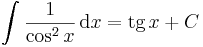
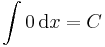
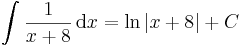
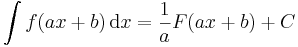
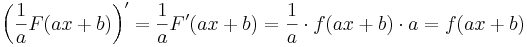
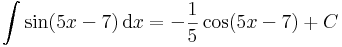
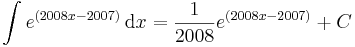
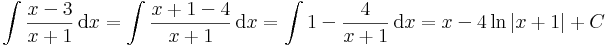
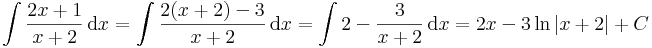
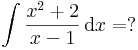
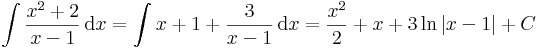
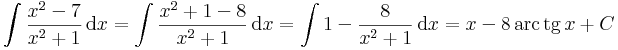
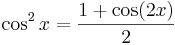
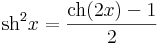
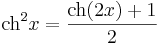
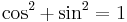
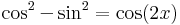
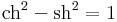
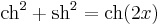
![\int\limits_{0}^{\pi}\sin^2 x\mathrm{d}x=\int\limits_{0}^{\pi}\frac{1-\cos(2x)}{2}\mathrm{d}x=\left[\frac{1}{2}x-\frac{1}{4}\sin(2x)\right]_0^\pi=\frac{\pi}{2}](/upload/math/b/b/1/bb1ac1a5fc003d49e4d0b180372d7001.png)
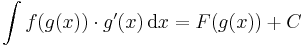
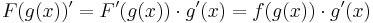
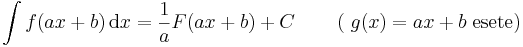
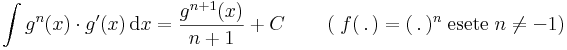
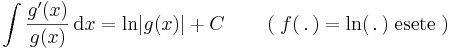
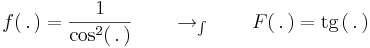
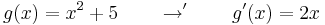
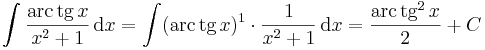
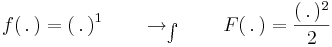
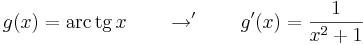
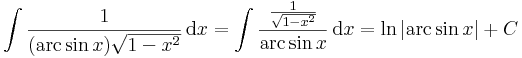
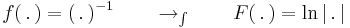
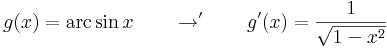
![\int x^2\sqrt[2008]{\mathrm{sh}\,x^3}\cdot \mathrm{ch}\,(x^3)\,\mathrm{d}x= \frac{1}{3}\int \sqrt[2008]{\mathrm{sh}\,x^3}\cdot (3x^2\mathrm{ch}\,(x^3))\,\mathrm{d}x=\frac{2008}{3\cdot 2009}(\mathrm{sh}\,x^3)^{\frac{2009}{2008}}+C](/upload/math/1/b/3/1b3c959834da02ddb24710fafb3e3b3e.png)