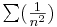Szerkesztő:Mozo/A2 szigorlat 4
Cauchy-féle gyökkritérium
Tétel. Legyen (an) valós számsorozat, ∑(an) pedig a belőle képezett sor. Ekkor
- ha
![\mbox{ }_{\mathrm{limsup}\sqrt[n]{|a_n|}<1}](/upload/math/2/a/2/2a2c0ff510cb6780177e06a528d0b021.png) , akkor ∑(an) abszolút konvergens
, akkor ∑(an) abszolút konvergens
- ha
![\mbox{ }_{\mathrm{limsup}\sqrt[n]{|a_n|}>1}](/upload/math/f/a/7/fa7619a6b425862203c91113c4990925.png) , akkor ∑(an) divergens
, akkor ∑(an) divergens
Bizonyítás
1. Legyen
Ekkor s = limsup(cn) a lismesz szuperrior fogalmának deifíciója szerint az |an| sorozat elemeinek n-edik gyökeinek (cn) sorozatának legnagyobb sűrűsödési pontja. Sűrűsödési pont, azaz s minden környezetében van a (cn) sorozatnak végtelen sok eleme, és a legnagyobb, mert nincs nála nagyobb sűrűsödési helye (cn)-nek.
s < 1 miatt vehetünk egy q számot úgy, hogy
- s < q < 1
Ekkor s "limsupsága" miatt egy adott M természetes számot követő minden n-re:
hiszen ha lenne végtelen sok elem, melyre ez nem telhesülne, akkor lenne s nél nagyobb sűrűsödési pont is. Tehát
azaz
De a (qn) mértani sorozatból képezett sor konvergens (hisz |q|<1), így a majoráns kritérium miatt a
sor is konvergens (merthogy a szóbanforgó mértani sor majorálja). Eszerint ∑(an) abszolút konvergens.
2. A másik esetben, minthogy s = limsup(cn), van olyan részsorozata (cn)-nek melynek minden eleme 1-nél nagyobb egyenlő:
ekkor viszont
és
de a szükséges kritérium miatt ha (an) (és vele együtt az összes részsorozata) nem a 0-hoz tart, akkor ∑(an) nem konvergens, márpedig a fenti olyan részsorozata (an)-nek, mely nem tarthat a 0-hoz, így ∑(an) nem konvergens.
Megjegyzések. A bizonyításból kiderül, hogy a tétel állításának második pontjánál többet is állíthatunk. Ha ugyanis van olyan részsorozata (cn)-nek melynek minden eleme 1-nél nagyobb egyenlő, már akkor is állíthatjuk, hogy ∑(an) nem konvergens. Ám az nem igaz, hogy ha limsup(cn) 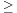 1, akkor ∑(an) nem konvergens, ellenpélda az
1, akkor ∑(an) nem konvergens, ellenpélda az
sor. Ez konverges, holott az n-edik gyökök sorozatának limesz szuperiorja 1.
Az előbb említett általános divergencia kritériumon túl azonban csak azt mondhatjuk, hogy ha limsup(cn) = 1, akkor további vizsgálatokat kell végeznünk, hogy döntésre juthassunk a konvergencia/divergencia kérdésében.
![c_n=\sqrt[n]{|a_n|}\,](/upload/math/b/3/c/b3c93c4892c869fcaa0541f02c6420cc.png)
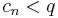
![\sqrt[n]{|a_n|} < q\,](/upload/math/8/e/d/8ed01181ef1c12da8e399eba5cdebaec.png)
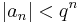
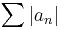
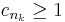
![\sqrt[n_k]{|a_{n_k}|} \geq 1\,](/upload/math/2/c/e/2ced0800302863bba53c806d141a7036.png)