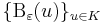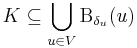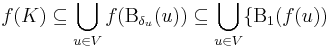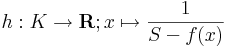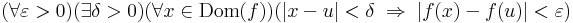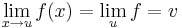Szerkesztő:Mozo/A2 szigorlat 5

Tétel – Bolzano-tétel – Intervallumon értelmezett, negatív és pozitív értékeket is felveő folytonos függvénynek van zérushelye.

a Bolzano-tételt még olymódon is szokás kimondani, hogy

intervallumon értelmezett folytonos függvény két függvényértéke között minden értéket fölvesz

melyet Darboux-tulajdonságnak neveznek. A Bolzano-tétel lényegében azt mondja ki, hogy az intervallumon folytonos függvények Darboux-tulajdonságúak. Megjegyezzük, hogy a Darboux-tétel pedig azt mondja ki, hogy az intervallumon differenciálható függvények deriváltfüggvénye Darboux-tulajdonságú.

Tétel – Weierstrass-féle minimum-maximum-elv – Korlátos és zárt intervallumon értelmezett folytonos függvény felveszi abszolút minimumát és maximumát.

Az alábbiakban felhasználjuk a kompaktság fogalmát.

(Kompakt egy K halmaz, ha minden nyílt halmazrendszerből, melynek uniója lefedi K-t kiválasztható véges sok nyílt halmaz is, melyek véges uniója még mindig lefedi K-t.)

Tétel (Weierstrass) Valós értékű, kompakt halmazon folytonos függvény felveszi minimumát és maximumát.

Azaz ha K⊆R^N kompakt és f ∈ C(K,R), akkor sup(f), inf(f) ∈ Ran(f)

Bizonyítás. 1) Először belátjuk, hogy kompakt halmazon folytonos függvény korlátos. Legyen ugyanis az ε=1 és f értelmezési tartománya K. A folytonosság miatt K minden u eleméhez létezik δ(u) pozitív szám, hogy f a B_δ(u) környezeten belül mindvégig az (f(u)-1;,f(u)+1) intervallumon belül marad. Ekkor a nyílt halmazokból álló

$\{\mathrm{B}_{\varepsilon}(u)\}_{u\in K}\,$

rendszer lefedi K-t, vagyis a Heine-Borel-tétel miatt már ebből véges sok is lefedi, azaz létezik V ⊆ K véges, hogy

$K\subseteq\bigcup\limits_{u\in V}\mathrm{B}_{\delta_{u}}(u)\,$

Ezek képei lefedik Ran(f)-et:

$f(K)\subseteq\bigcup\limits_{u\in V}f(\mathrm{B}_{\delta_{u}}(u))\subseteq\bigcup\limits_{u\in V}\{\mathrm{B}_{1}(f(u))\,$

Ez utóbbi a folytonosság miatt, tehát f képét véges sok korlátos intervallum lefedi, azaz korlátos.

2) Belátjuk, hogy f felveszi a szuprémumát (és ugyanígy az infimumát is). Legyen S := sup(f) (azaz f értékkészletének legkisebb felső korlátja). Ekkor a g : K $\to$ R, x $\mapsto$ S-f(x) függvény nemnegatív értékeket vesz föl. Ha f nem venné fel a szuprémumát, akkor g pozitív lenne. Ekkor értelmezhető lenne a

$h:K\to\mathbf{R};x\mapsto \frac{1}{S-f(x)}$

függvény. h mert folytonos függvényekből van folytonosságot megőrző módon összetéve. Az 1) pont szerint korlátos is, ami azonban ellentmond annak, hogy S a szuprémum. Ugyanis S = sup Ran(f) azt jelenti, hogy minden 1/n alakú számra van x_n ∈ K, hogy | S − f(x_n) | < 1 / n, azaz van olyan K-beli x_n sorozat, melynek képsorozata h által a végtelenbe tart, azaz h nem korlátos.

Tétel (Bolzano) Összefüggő halmaz folytonos képe összefüggő.

(Ha f ∈ C(Rⁿ,R^m), Dom(f) ívszerűen összefüggő, akkor Ran(f) is ívszerűen összefüggő.)

Bizonyítás. Az ívszerű összefüggőségből és a folytonos függvények kompozíciójára vonatkozó tételből.

Azt mondjuk, hogy az f: R 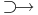$\supset\!\to$ R függvény folytonos az értelmezési tartománya egy u pontjában, ha

$(\forall \varepsilon>0)(\exists \delta>0)(\forall x\in \mathrm{Dom}(f))(|x-u|<\delta\;\Rightarrow\;|f(x)-f(u)|<\varepsilon)$

Folytonos egy függvény, ha az értelmezési tartománya minden pontjában folytonos

Legyen f egy az A ⊆ R halmazon értelmezett, R-be képező függvény. Legyen 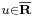$\scriptstyle{u\in \overline{\mathbf{R}}}$ az A torlódási pontja. Azt mondjuk, hogy az f-nek a $\scriptstyle{v\in \overline{\mathbf{R}}}$ elem határértéke az u-ban, ha

minden ε > 0 esetén létezik olyan δ > 0, hogy minden x ∈ A ∩ B_δ(u)\{u}-re f(x) ∈ B_ε(v)

ahol természetesen a +∞ és -∞ környezetei a már említett módon értendők.

Ebben az esetben a határérték egyértelmű és jelölése:

$\lim\limits_{x\to u}f(x)=\lim\limits_{u}f=v\,$

Folytonosság és határérték kapcsolata

A folytonosságot, csak az értelmezési tartomány pontjaiban nézhetünk, hisz a definícióban f(u) is szerepel. Ellenben határértéket akár azon kívüli is nézhetünk (sőt!). Mégis, a két fogalom között szoros kapcsolat van:

1. Tétel. -- Folytonos függvény határértéke a helyettesítési értéke -- Legyen az u az f értelmezési tartományában. Ekkor a következők ekvivalensek egymással:

1. f folytonos u-ban
2. u izolált pontja Dom(f)-nek, vagy u torlódási pontja Dom(f)-nek, létezik u-an határértéke és lim_uf = f(u)

2. Tétel. -- Véges helyen véges határértékű függvény folytonossá tehető -- Legyen u a Dom(f) véges torlódási pontja és v véges (R-beli) szám. Ekkor a következők ekvivalensek.

1. $\exists\lim\limits_{u}f=v\,$
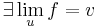
2. létezik az f-nek olyan 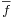$\scriptstyle{\overline{f}}$ u-ban folytonos kiterjeszétse (vagy módosítása), hogy

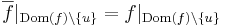   $\overline{f}|_{\mathrm{Dom}(f)\setminus \{u\}}=f|_{\mathrm{Dom}(f)\setminus \{u\}}$ és $\overline{f}(u)=v\,$

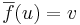
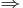Definíció Legyen D ⊆ R^N, f: D $\to$ R^M, A ∈ R^M, u ∈ R^N torlódási pontja D-nek. Azt mondjuk, hogy az f függvény határértéke az u pontban az A, ha ∀ε>0 ∃δ>0 ∀x∈D x ∈ B_δ(u) $\Rightarrow$ B_ε(A)

Az, hogy a határérték az u-ban A azt jelenti, hogy a függvénynek folytonos kiterjesztése u-ban az f(u) = A hozzárendelés.

Lényeges, hogy tudjuk annak jellemzését, hogy egy pontban a határérték nem létezik. Ehhez a Heine-féle határértékfogalmat használjuk:

Tétel. Legyen D ⊆ R^N, f: D $\to$ R^M, A ∈ R^M, u ∈ R^N torlódási pontja D-nek. Ekkor az alábbi két kijelentés ekvivalens egymással:

1. létezik $\lim\limits_{u} f=A$,
2. $(\forall (a_n)\in\mathrm{Dom}(f)\setminus\{u\}^{\mathbf{Z}^+})(a_n\to u\quad\Rightarrow\quad f(a_n)\to A)$

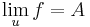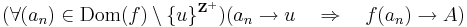
Ezzel megfogalmazhatjuk annak a feltételét, hogy nem létezik a határérték:

Tétel. Legyen D ⊆ R^N, f: D $\to$ R^M, A ∈ R^M, u ∈ R^N torlódási pontja D-nek. f-nek nincs határértéke u-ban, ha

létezik olyan 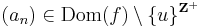$(a_n)\in\mathrm{Dom}(f)\setminus\{u\}^{\mathbf{Z}^+}$ sorozat, hogy bár 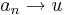$a_n\to u$, de (f(a_n)) nem konvergens.