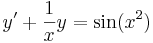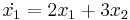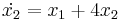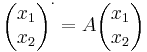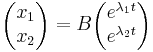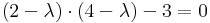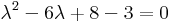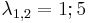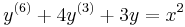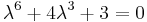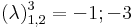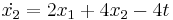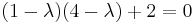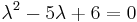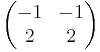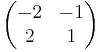Szerkesztő:Mozo/A3 gyakorló feladatok 2.
Tartalomjegyzék |
Lineáris helyettesítés
Mi az általános megoldása?
Mo.
Legyen u=2x+4y, ekkor du=2dx+4dy, azaz
Innen:
Implicit általános megoldás:
Kezdeti érték probléma
Oldjuk meg az
egyenletet az
- a)
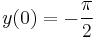
- b)
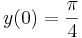
- c)
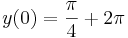
kezdeti feltételekkel.
1. Mo.
Nem egzakt:
Egzakttá tehető, ugyanis:
Emiatt
Megoldása:
2. Mo.
Persze szeparábilis is:
a) Ez egy konstans megoldás (y(x)=π/2) és nincs másik a (0,π/2)-n áthaladó, mert az y szerinti parciális derivált korlátos.
b) Az általános megoldásból keressük a kezdeti feltételt kielégítő megoldást:
Az implicit egyenlet:
- cos − 3y = x3 + 3C
Ha x=0 és y=π/4, akkor
és
c) ugyanez + 2π
HF. Oldjuk meg az y' = sin(x) yln(y) egyenletet az
- a) y(0)=1,
- b) y(0)=e
kezdeti feltételek mellett!
Függvényegyütthatós lineáris, állandó variálása
Kezdeti értékes állandó együtthatós lineáris
Homogén lineáris differenciál egyenlet rendszer
Mo. Ha a feladat
alakú különböző valós sajátértékekkel, és az A-nak λ1, λ2-hoz tartozó sajátvektoraiból álló mátrix:
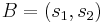 ,
,
akkor a megoldás
Itt a sajátértékefeladat megoldása:
azaz
6.
Mo.
Kar. egy:
-1, -3 háromszoros gyökök, tehát:
- ya = c1e − x + c2xe − x + c3x2e − x + c4e − 3x + c5xe − 3x + c6x2e − 3x
A próbafüggvény: y=Ax2+Bx+C, tehát:
- 4Ax2 + 4Bx + 4C = x2
azaz A=1/4, B=C=0.
Inomogén lineáris differenciál egyenlet rendszer
Mo.
Homogén:
Sajátértékek:
Sajátvektorok:
Innen:
Innen:
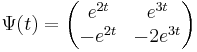 , és c=(c_1,c_2)-vel
, és c=(c_1,c_2)-vel
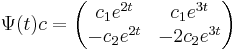
Inhomogén:
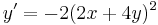
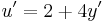
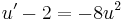
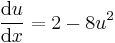
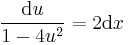
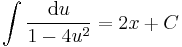
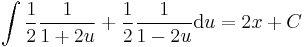
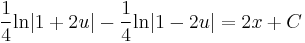
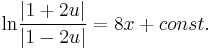
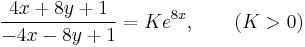
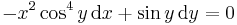
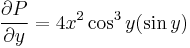
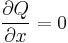
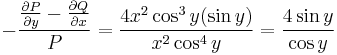
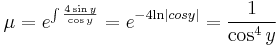
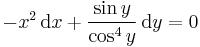
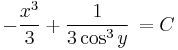
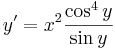
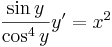
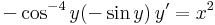
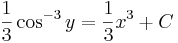
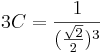
![y(x)=\mathrm{arccos}\frac{1}{\sqrt[3]{x^3+\frac{24}{(\sqrt{2})^3}}}](/upload/math/2/d/0/2d00fc36a69b3e76ac5fef5e80c7a2a3.png)