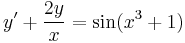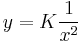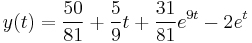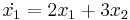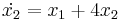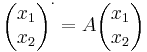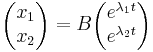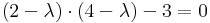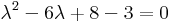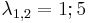Szerkesztő:Mozo/A3 gyakorló feladatok 3.

A MathWikiből
(Változatok közti eltérés)
(→Másodrendű lineáris kezdetiérték feladat)
(→Elsőrendű lineáris egyenletrendszer)
50. sor: 50. sor:
 
:<math>
 
:<math>
 
y(t)=\frac{50}{81}+\frac{5}{9}t+\frac{31}{81}e^{9t}-2e^t</math>
 
y(t)=\frac{50}{81}+\frac{5}{9}t+\frac{31}{81}e^{9t}-2e^t</math>
−
===Elsőrendű lineáris egyenletrendszer===
+
===Homogén lineáris d. egyenletrendszer===
 +
:<math>\dot{x_1}=2x_1+3x_2</math>
 +
:<math>\dot{x_2}= x_1+4x_2</math>
 +
 
 +
''Mo.'' Ha a feladat
 +
:<math>\begin{pmatrix}x_1\\x_2\end{pmatrix}^{\cdot}=A\begin{pmatrix}x_1\\x_2\end{pmatrix}</math>
 +
alakú különböző valós sajátértékekkel, és az A-nak &lambda;<sub>1</sub>, &lambda;<sub>2</sub>-hoz tartozó sajátvektoraiból álló mátrix:
 +
:<math>B=(s_1,s_2)\,</math>,
 +
akkor a megoldás
 +
:<math>\begin{pmatrix}x_1\\x_2\end{pmatrix}=B\begin{pmatrix}e^{\lambda_1t}\\e^{\lambda_2 t}\end{pmatrix}</math>
 +
Itt a sajátértékefeladat megoldása:
 +
:<math>(2-\lambda)\cdot (4-\lambda)-3=0\,</math>
 +
azaz
 +
:<math>\lambda^2-6\lambda+8-3=0\,</math>
 +
:<math>\lambda_{1,2}=1;5\,</math>

A lap 2013. október 13., 22:01-kori változata

Tartalomjegyzék

Lineáris differenciálegyenletek

Függvényegyütthatós elsőrendű lineáris d.e.

y'+\frac{2y}{x}=\sin(x^3+1)

Mo. Homogén megoldása. y=0 konstans megoldás.

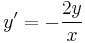
y'=-\frac{2y}{x}
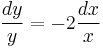
\frac{dy}{y}=-2\frac{dx}{x}
ln | y | = ln | x | − 2 + C

Bolzano tétele miatt tetszőleges K valós számmal:

y=K\frac{1}{x^2}

ami a homogén általános megoldása.

Inhomogén part. keresése

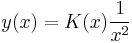
y(x)=K(x)\frac{1}{x^2}
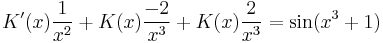
K'(x)\frac{1}{x^2}+K(x)\frac{-2}{x^3}+K(x)\frac{2}{x^3}=\sin(x^3+1)
K'(x) = x2sin(x3 + 1)
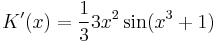
K'(x)=\frac{1}{3}3x^2\sin(x^3+1)
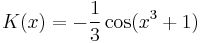
K(x)=-\frac{1}{3}\cos(x^3+1)
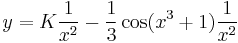
y=K\frac{1}{x^2}-\frac{1}{3}\cos(x^3+1)\frac{1}{x^2}

Másodrendű lineáris kezdetiérték feladat

y''-10y'+9y=5t,\quad\quad y(0)=-1,\;y'(0)=2

Mo.

L(y') = sY − y(0)
L(y'') = s2Y − sy(0) − y'(0)
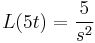
L(5t)=\frac{5}{s^2}
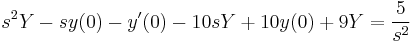
s^2Y-sy(0)-y'(0)-10sY+10y(0)+9Y=\frac{5}{s^2}
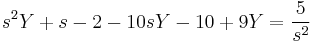
s^2Y+s-2-10sY-10+9Y=\frac{5}{s^2}
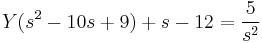
Y(s^2-10s+9)+s-12=\frac{5}{s^2}
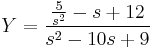
Y=\frac{\frac{5}{s^2}-s+12}{s^2-10s+9}
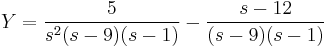
Y=\frac{5}{s^2(s-9)(s-1)}-\frac{s-12}{(s-9)(s-1)}
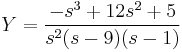
Y=\frac{-s^3+12 s^2+5}{s^2(s-9)(s-1)}
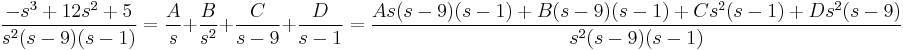
\frac{-s^3+12 s^2+5}{s^2(s-9)(s-1)}=\frac{A}{s}+\frac{B}{s^2}+\frac{C}{s-9}+\frac{D}{s-1}=\frac{As(s-9)(s-1)+B(s-9)(s-1)+Cs^2(s-1)+Ds^2(s-9)}{s^2(s-9)(s-1)}

A gyököket beírva: s=0-ra B=5/9

s=1-re D=16/(-8)=-2

s=9-re C.8.81=-243+12.27+5 C=31/81

s=2-re A=50/81

Visszatranszf.

y(t)=\frac{50}{81}+\frac{5}{9}t+\frac{31}{81}e^{9t}-2e^t

Homogén lineáris d. egyenletrendszer

\dot{x_1}=2x_1+3x_2
\dot{x_2}= x_1+4x_2

Mo. Ha a feladat

\begin{pmatrix}x_1\\x_2\end{pmatrix}^{\cdot}=A\begin{pmatrix}x_1\\x_2\end{pmatrix}

alakú különböző valós sajátértékekkel, és az A-nak λ1, λ2-hoz tartozó sajátvektoraiból álló mátrix:

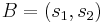B=(s_1,s_2)\,,

akkor a megoldás

\begin{pmatrix}x_1\\x_2\end{pmatrix}=B\begin{pmatrix}e^{\lambda_1t}\\e^{\lambda_2 t}\end{pmatrix}

Itt a sajátértékefeladat megoldása:

(2-\lambda)\cdot (4-\lambda)-3=0\,

azaz

\lambda^2-6\lambda+8-3=0\,
\lambda_{1,2}=1;5\,
A lap eredeti címe: „http://wiki.math.bme.hu/index.php?title=Szerkeszt%C5%91:Mozo/A3_gyakorl%C3%B3_feladatok_3.&oldid=9191”
Személyes eszközök