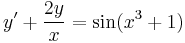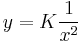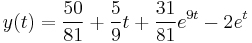Szerkesztő:Mozo/A3 gyakorló feladatok 3.

Lineáris differenciálegyenletek

Függvényegyütthatós elsőrendű lineáris d.e.

$y'+\frac{2y}{x}=\sin(x^3+1)$

Mo. Homogén megoldása. y=0 konstans megoldás.

$y'=-\frac{2y}{x}$

$\frac{dy}{y}=-2\frac{dx}{x}$

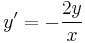
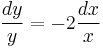
ln | y | = ln | x | ^{− 2} + C

Bolzano tétele miatt tetszőleges K valós számmal:

$y=K\frac{1}{x^2}$

ami a homogén általános megoldása.

Inhomogén part. keresése

$y(x)=K(x)\frac{1}{x^2}$

$K'(x)\frac{1}{x^2}+K(x)\frac{-2}{x^3}+K(x)\frac{2}{x^3}=\sin(x^3+1)$

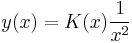
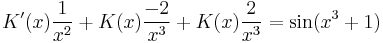
K'(x) = x²sin(x³ + 1)

$K'(x)=\frac{1}{3}3x^2\sin(x^3+1)$

$K(x)=-\frac{1}{3}\cos(x^3+1)$

$y=K\frac{1}{x^2}-\frac{1}{3}\cos(x^3+1)\frac{1}{x^2}$

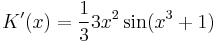
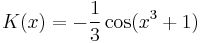
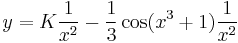
Másodrendű lineáris kezdetiérték feladat

$y''-10y'+9y=5t,\quad\quad y(0)=-1,\;y'(0)=2$

Mo.

L(y') = sY − y(0)

L(y'') = s²Y − sy(0) − y'(0)

$L(5t)=\frac{5}{s^2}$

$s^2Y-sy(0)-y'(0)-10sY+10y(0)+9Y=\frac{5}{s^2}$

$s^2Y+s-2-10sY-10+9Y=\frac{5}{s^2}$

$Y(s^2-10s+9)+s-12=\frac{5}{s^2}$

$Y=\frac{\frac{5}{s^2}-s+12}{s^2-10s+9}$

$Y=\frac{5}{s^2(s-9)(s-1)}-\frac{s-12}{(s-9)(s-1)}$

$Y=\frac{-s^3+12 s^2+5}{s^2(s-9)(s-1)}$

$\frac{-s^3+12 s^2+5}{s^2(s-9)(s-1)}=\frac{A}{s}+\frac{B}{s^2}+\frac{C}{s-9}+\frac{D}{s-1}=\frac{As(s-9)(s-1)+B(s-9)(s-1)+Cs^2(s-1)+Ds^2(s-9)}{s^2(s-9)(s-1)}$

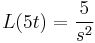
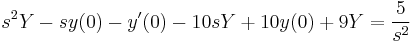
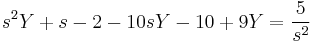
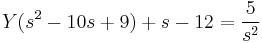
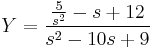
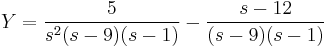
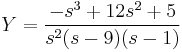
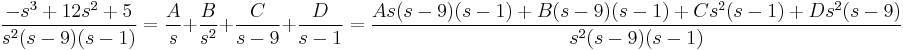
A gyököket beírva: s=0-ra B=5/9

s=1-re D=16/(-8)=-2

s=9-re C.8.81=-243+12.27+5 C=31/81

s=2-re A=50/81

Visszatranszf.

$y(t)=\frac{50}{81}+\frac{5}{9}t+\frac{31}{81}e^{9t}-2e^t$