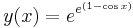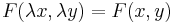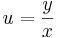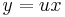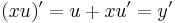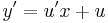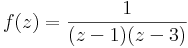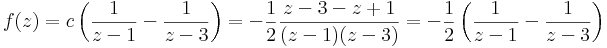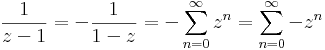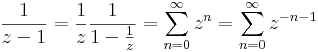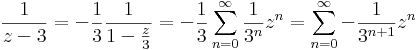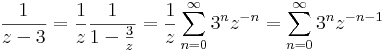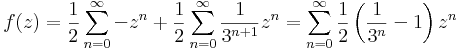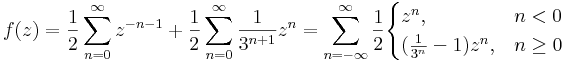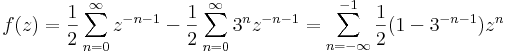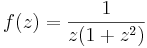A3 2009 gyak 2
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) |
||
| 32. sor: | 32. sor: | ||
:<math>y'=u'x+u\,</math> | :<math>y'=u'x+u\,</math> | ||
| − | '''2.''' Oldjuk meg az | + | '''2.''' Oldjuk meg az |
| + | :<math>y'xy^3=x^4+y^4</math> | ||
| + | egyenletet! | ||
| + | ''Mo.'' Általános megoldás: | ||
| + | :<math>(u'x+u)xu^3x^3=x^4+u^4x^4</math> | ||
| + | :<math>u'x+u^4=1+u^4</math> | ||
| + | :<math>u'x=1</math> | ||
| + | :<math>u'=\frac{1}{x}</math> | ||
| + | :<math>\frac{u^2}{2}=\mathrm{ln}\,|x|+C</math> | ||
| + | |||
| + | |||
| + | |||
| + | <!-- | ||
<math>y'x=y+\sqrt{x^2+y^2}\,</math> | <math>y'x=y+\sqrt{x^2+y^2}\,</math> | ||
egyenletet! | egyenletet! | ||
| 44. sor: | 56. sor: | ||
:<math>\mathrm{arsh}\,y=-\mathrm{ln}\,|x|+C</math> negatív x-re | :<math>\mathrm{arsh}\,y=-\mathrm{ln}\,|x|+C</math> negatív x-re | ||
| − | + | ||
:<math>\frac{1}{2}\mathrm{ln}\,1+u^2=c+\mathrm{ln}\,|x|\,</math> itt ''c'' tetszőleges valós szám | :<math>\frac{1}{2}\mathrm{ln}\,1+u^2=c+\mathrm{ln}\,|x|\,</math> itt ''c'' tetszőleges valós szám | ||
:<math>\mathrm{ln}\sqrt{1+u^2}=\mathrm{ln}\,C|x|\,</math> itt ''C'' tetszőleges pozitív szám éspedig ln ''c'' = ''C''. | :<math>\mathrm{ln}\sqrt{1+u^2}=\mathrm{ln}\,C|x|\,</math> itt ''C'' tetszőleges pozitív szám éspedig ln ''c'' = ''C''. | ||
| 115. sor: | 127. sor: | ||
:d) <math>r(z)=\frac{1}{\sin 2z}</math> | :d) <math>r(z)=\frac{1}{\sin 2z}</math> | ||
függvények 0-beli reziduumát, egységkörön vett integrálját és szakadásának jellegét! | függvények 0-beli reziduumát, egységkörön vett integrálját és szakadásának jellegét! | ||
| − | + | --> | |
==Laurent-sorfejtés== | ==Laurent-sorfejtés== | ||
'''5.''' Határozzuk meg az | '''5.''' Határozzuk meg az | ||
| 149. sor: | 161. sor: | ||
:<math>f(z)=\frac{1}{z(1+z^2)}\,</math> | :<math>f(z)=\frac{1}{z(1+z^2)}\,</math> | ||
függvényt! | függvényt! | ||
| − | |||
A lap 2009. november 19., 16:59-kori változata
Szeparábilis differenciálegyenlet
1. Oldjuk meg az
egyenletet az
- a)
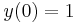
- b)
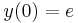
kezdeti feltételek mellett!
Mo. a) Az egyenlet konstans megoládsa az y(x)=1. Ez a kezdeti feltételnek megfelel.
b) Az általános megoldásból keressük a kezdeti feltételt kielégítő megoldást:
ez az implicit egyenlet. Ha x=0 és y=e, akkor
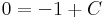 ,
, 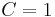
és
Megjegyzés. Minden R× R+-beli kezdeti feltételre egyértelműen létezik a megoldás.
Homogén fokszámú egyenlet
Azt mondjuk, hogy az y' = F(x,y) egyenlet homogén fokszámú, ha
A homogén fokszámú egyenlet megoldása visszavazethető a szeparálásra az
új változó bevezetésével, ahol u = u(x) az ismeretlen függvény. Tehát:
Ekkor
azaz
2. Oldjuk meg az
- y'xy3 = x4 + y4
egyenletet! Mo. Általános megoldás:
- (u'x + u)xu3x3 = x4 + u4x4
- u'x + u4 = 1 + u4
- u'x = 1

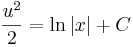
Laurent-sorfejtés
5. Határozzuk meg az
nulla körüli Laurent-sorait!
Mo.
alkalmas tehát a c=-1/2.
Ha |z|<1, akkor
Ha |z|>1, akkor
A másik tag:
Ha |z/3|<1, azaz |z|<3
Ha |z|>3 , akkor
Tehát a Laurent-sorok:
|z|<1 esetén reguláris:
1<|z|<3 esetén vegyes:
|z|>3 esetén csak főrész:
HF Fejtsük sorba a 0 körül az
függvényt!